線形単回帰分析について
線形単回帰分析
こんにちは!わいわわです!
前回は相関係数を学習し2つのデータの関係性を求めていきました。
今回のテーマは「回帰分析によって数値を予測する」です!
頑張っていきましょう!
線形回帰分析
回帰分析とは、数値を予測する分析です。
回帰は「あることが行われて、また元と同じ状態に戻ること」を言います。
線形回帰...説明変数に対して、目的変数が線形に近い値で表される状態のこと
この線形回帰を用いて回帰分析を行うことを線形回帰分析という!
モデリング
データ分析や機械学習の根底にあるのは「統計的なモデリング」の考え方です。
モデリング...具体的なデータを数式や数理的な表現に移し替えてモデルを構築する作業
構築されたモデルは「計算式の塊」で、データを入力すると予測結果が出力されます。
モデリングをする際に最初に考えるべきことは、何を変数として扱うかです。
ここでの変数とは「何らかの変化する値」のことを指します。
目的変数
目的変数とは予測の対象となる変数のことです。
「30日間の最高気温と清涼飲料売上数」の場合は清涼飲料水売上数が目的変数になります。
(モデルとしては最高気温を元に売り上げを予測するからです)
目的変数はこのように大小の値をとることもありますが
分類を示すカテゴリーデータの場合もあります。
カテゴリーデータには「0か1か」「yesかnoか」のように
2つの分類項目を持つ場合(二値分類)と、3つ以上の分類項目を持つ場合(多値分類)があります。
目的変数を予測する場合、
回帰問題...数値が対象
分類問題...カテゴリーデータが対象
と呼ばれます。
説明変数
説明変数とは目的変数の変化を説明する変数のことです。
上記の例だと説明変数は「最高気温」になります。
機械学習の分野ではデータの特徴を数値化したものを特微量と呼びます。
線形単回帰モデル
相関関係のある2つのデータを用いて傾向をつかむには
2つのデータの散布図に描かれたプロットの中心を通るような直線を引きます。
この直線のことを回帰直線と呼び、回帰直線でモデル化する分析を
線形回帰分析と呼びます!
この回帰直線を引くには「各店とのズレが最小となる位置を通る」ことが必要です。
y = ax+b
xは「説明変数」yは「目的変数」で、この式を立てて検証をします。
「a」は回帰係数と呼ばれ、直線の傾きを表します。
bは切片で、xが0の時のyの値です。
このaとbを求めることで線形回帰分析を検証できます。
回帰係数aと切片bは「線形単回帰モデルが出力する予測値と目的変数との差の二乗和が最小になる」
ような方法で推測されますが、これは最小二乗法と呼ばれます。
式を簡単にするために、まずは切片のbを抜いて、最小二乗法を求めます。
import numpy as np
def lineareg(x, y):
a = np.dot(x, y) / (x**2).sum()
return a
関数lineareg()関数を作成し、回帰係数aを計算して戻り値を返しています。
このx,yを定義して、回帰係数aを求めると
x = np.array([1, 2, 4, 6, 7, 9])
y = np.array([1, 3, 4, 5, 7, 10])
a = lineareg(x, y)
a
出力結果→1.0267379679144386
説明変数xと目的変数yが交わる点をプロットして散布図を作成し、
求めた回帰係数aを使って回帰直線を散布図上に描画します。
import matplotlib.pyplot as plt
plt.scatter(x, y, color='black')
xm = x.max()
plt.plot([0, xm], [0, a*xm], color='red')
plt.show()
!出力結果!
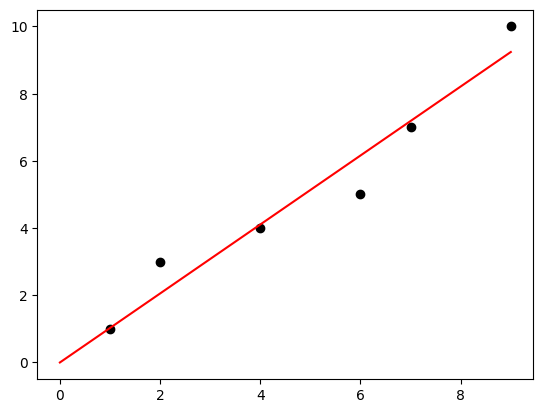
この線が、回帰直線ですね!
bの傾きは計算を簡単にするため抜いている、回帰直線です。
最小二乗法を出す
前回同様、8月各日の最高気温及びその日に売れた飲料水の売上数を記録したデータの
最高気温,清涼飲料売上数
26,84
25,61
26,85
24,63
25,71
24,81
26,98
26,101
25,93
27,118
...
カンマ区切りのデータが30個(30日分)を使用し、
回帰係数aと切片bを実際に求めます。
import pandas as pd
# CSVファイルのデータをデータフレームに読み込む
df = pd.read_csv('sales.csv')
# '最高気温'列のデータをNumPy配列として取得
x = df['最高気温'].values
# '清涼飲料売上数'列のデータをNumPy配列として取得
y = df['清涼飲料売上数'].values
import numpy as np
def lineareg(x, y):
Args:
x (ndarray): 説明変数
y (ndarray): 目的変数
Returns:
a(float): 回帰係数
b(float): 切片
"""
n = len(x)
# 回帰係数を求める
a = (np.dot(x, y)-(y.sum()*x.sum() / n)
) / ((x**2).sum() - x.sum()**2 / n)
# 切片を求める
b = (y.sum()-a*x.sum())/n
return a, b
a, b = lineareg(x, y)
# 回帰係数を出力
print(a)
# 切片の値を出力
print(b)
!出力結果!
33.74080524536438
-760.8771642249819
散布図を描画し、線形単回帰モデルの式「y=ax+b」を使って回帰直線を描いてみます。
import matplotlib.pyplot as plt
plt.scatter(x, y, color='black')
plt.plot(
[0, x.max()],
[b, a*x.max() + b],
color='red')
# x軸とy軸のスケールを設定
plt.axis([
x.min()-1, x.max()+1,
0, y.max()+20])
plt.show()
!出力結果!
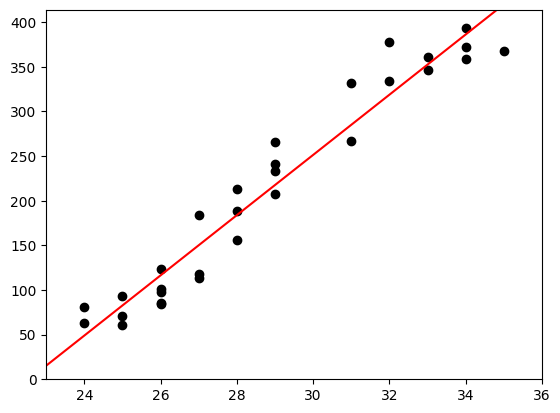
回帰直線は、x軸の始点を0、終点を最高気温の最大値に設定し、
y軸の始点を切片bの値、終点を
回帰係数a × 最高気温の最大値 + 切片b
で求めた値に設定して、描画します。
最後に、この単回帰モデルの式に日々の最高気温xを代入して予測値を求めます。
y_pred = a*x + b
print(y_pred)
!出力結果!
[116.38377215 82.64296691 116.38377215 48.90216166 82.64296691
48.90216166 116.38377215 116.38377215 82.64296691 150.1245774
150.1245774 116.38377215 183.86538265 183.86538265 150.1245774
183.86538265 217.60618789 217.60618789 217.60618789 285.08779838
285.08779838 217.60618789 318.82860363 352.56940887 386.31021412
352.56940887 386.31021412 420.05101936 318.82860363 386.31021412]
決定係数
出力されたグラフを見ると、単回帰モデルは実測値をうまく予想しているように見えます。
が、グラフだけでは曖昧なことしか言えません。
そこで「単回帰式がどの程度の確率で信頼できるのか」を評価する決定係数という指標があります。
以下で求めることができます。
1-((y-(a*x+b))**2).sum() / (
(y-np.mean(y))**2).sum()
!出力結果!
0.9413818994683985
「0.9413...」なのでかなり精度が高いことになります。
所感
教科書的なデータを用いたので今回は精度が高くなりましたが
実際の業務では決定係数0.9を下回ることが多いみたいです!
なんとなく超簡単なAIを作れたみたいでうれしいです!
Discussion