数値データの特微量エンジニアリング(基礎)
予測問題におけるモデリングを学習
こんにちは!わいわわです。
参考書でAI、pythonについての学習をしていますが、
今回からモデリングに入っていきます。
以前、ざっくりと前処理について学習しましたが、
今回からは数値を扱いながら、学習していきます!
前処理
分析するデータはそのままの状態で分析にかけられることもありますが
一部のデータが欠落していたり、データのサイズが大きすぎるなど、
そのままの状態では分析にかけられないことも多いです。
そのようなデータを前処理することで分析にかけられるようにします。
この前処理のことを特微量エンジニアリングと呼びます。
特微量エンジニアリングで行うこと
・データの欠落した値(欠損値)を適切な値に置き換える
・外れ値の処理
・データの整形(散らばり具合の調整など)
・データの形式が適切でない場合の変換
欠損値の処理
CSVファイルのデータをPandasのデータフレームに読み込んだとき、
何も入力されていない箇所があると欠損値と見なされてNaNと表示されます。
予測モデルのアルゴリズムである「決定木」「ランダムフォレスト」では
欠損値そのものに意味をもたせることでそのまま扱うことができますが、
一方で回帰による予測モデルでは欠損値があると分析に支障があるので
状況に応じて次の操作を行って対処することになります。
・代表値で置き換える
・他の行のデータから欠損値を予測して補完する
・欠損値のある行ごと削除する
欠損値を代表値で置き換える
欠損値をなくす方法のうち、最もシンプルでよく使われるのが
「欠損値が存在する列の代表値で埋める」というものです。
欠損がランダムで発生しているときに特に有効です。
実際に平均値で埋め込む
一般的によく知られている代表値に平均値があります。
欠損値が存在する列の平均を求め、欠損している箇所にその値を埋め込みます。
PandasのDataFrame.fillna()メソッドは引数に指定した値を欠損値と置き換えます。
df.fillna(df.mean())とした場合、すべての欠損値が列の平均値で置き換えられます。
[scoring.csv]
A,B
70,80
70,75
70,80
,85
90,85
70,90
80,75
70,
70,
85,90
今回はこの、欠損値のあるファイルを用意し実演してみます。
import pandas as pd
df = pd.read_csv('scoring.csv')
df
!出力結果!

ちゃんとNaNで表示されていますね。
ではここからdf.fillna(df.mean())を使用します。
df.fillna(df.mean())
!出力結果!

3Aが75.0に、B7、B8が82.5に置き換わりました。
これはそれぞれAの平均値とBの平均値ですね!
欠損値を中央値または対数変換後の平均値で埋め込む
商品価格や年収のように、データの分布に偏りがあったり
突出した外れ値が存在する場合は平均ではなく中央値を使うのが常套手段です。
中央値はmedian()で出力できます。
df.fillna(df.median())
!出力結果!
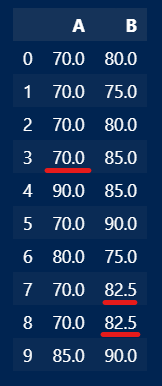
線を引いた部分がその列の中央値になっていますね!
元のデータフレームを変更する
では、欠損値を補完できたので、置き換えた状態で保存したいです。
そのためには
df = df.fillna(df.median)
のように代入を行うかもしくは
df.fillna(df.median(), inplace=True)
のように引数に「inplace=True」を設定します。
欠損値がある行ごと削除する
欠損値がある行ごと削除してしまう、あるいは欠損値がある列ごと削除してしまう方法。
データの量が十分にあり、欠損値を含むデータを除外しても
分析上影響がでないと判断できれば使用してもよいです。
PandasのDataFrame.dropna()メソッドは
df.dropna(axis=0)
とすると欠損値が存在する行データをすべて削除します。
axis=0は処理対象の軸を行にするためのオプションですが、
デフォルト値なので省略してもかまいません!
df.dropna(axis=1)
とした場合は処理の対象が列となり、欠損値が存在する列データをすべて削除します。
外れ値の処理
データにはまれに極端に大きい(または小さい)値が含まれていることがあり、
そういったほかのデータから離れた外れ値があると予測の精度を低下させる要因になります。
外れ値を取り除く方法として単純に外れ値が含まれるデータをレコードごと削除する方法がありますが、
何をもって外れ値とするか、を決めておくことが必要です。
対数変換
標準化を行うと、スケーリングされることでデータの分布が伸縮します。
元のデータを正規分布により近似させるという特微量エンジニアリングとして
対数変換を行います。
対数変換は対象のデータの値を変えるという意味ではスケール変換と同じですが、
対数変換ではデータの分布が変化します。
データのスケールが大きい時はその範囲が縮小され、
スケールが小さい時は拡大されるように変化します。
これによって山のある分布に近づけたり、裾の長い分布に近づけたりします。
対数変換の際は、log(x+1)のように1を加えてから対数をとります。
import numpy as np
x = ([1.0, 10.0, 100.0, 1000.0, 10000.0])
np.log1p(x)
!出力結果!
array([0.69314718, 2.39789527, 4.61512052, 6.90875478, 9.21044037])
所感
今回は機械学習におけるデータの前処理を学習しました。
数値データの際の補完の仕方が分かり、よりイメージがつきました。
言葉の場合どうするのか、という点も気になりますが、
引き続き学習を進めていきます!
Discussion