緯度、経度から三次元空間上の座標を取得する!
はじめに
FrightRadar24みたいな奴を3Dで作る!という事で、前回は地球をつくりました。
今回は与えられた緯度、経度から三次元空間上の座標(x,y,z)を求めたいと思います。
環境はNext.js + Three.js + React-three-fiberです。
サポートライブラリでdreiも使っています。カメラ制御とか色々便利な物が入っています。
試行錯誤
関数を作る
数学は勉強してこなかったので、まずはGoogleで検索しました。複数サイトだったり、ブログだったりでます。参考にしながら作っていきましょう。
最も参考にしたのは国土地理院でした。
数式が載っているので参考にしながら、、、
function getCoordinatesFromLatLon(lat: number, lon: number): Vector3{
//ラジアンに変換
const φ = lat * Math.PI / 180;
const λ = lon * Math.PI / 180;
//地球の半径は今回100で設定したので
const r = 100;
//扁平率
const f = 1.0 / 298.257222101;
//第一離心率
const e = Math.sqrt( 2 * f - f * f );
const e2 = e * e;
const sini = Math.sin(φ);
const W = Math.sqrt( 1 - e2 * sini * sini);
//卯酉線曲率半径
const N = r / W;
const x = N * Math.cos(φ) * Math.cos(λ);
const y = N * Math.cos(φ) * Math.sin(λ);
const z = N * (1 - e2) * Math.sin(φ);
return new Vector3(x, y, z);
}
地球は球体ではなかった
まずは関数では地球を完全な球としてではなくほんの少し歪んだ楕円体として計算しました。
なので扁平率を使って地球を歪ませておきます。
赤道を通る線が少し膨らんでいるので
//扁平率
const flattening = 1 + 1 / 298.257223563
.
.
.
<mesh castShadow position={[0, 0, 0]} scale={[1, flattening ,1]}>
<sphereGeometry args={[100, 128, 64]}/>
<meshPhysicalMaterial map={earthMap}/>
</mesh>
.
.
.
およそ300分の1の歪みなので目視ではわかりませんが、計算の誤差を減らすためにやっておきます。
ズレる
作った関数にGoogleMapから拝借した羽田空港の緯度経度を渡し、座標を取得します。
その座標に小さい球をピンとして表示してみます。
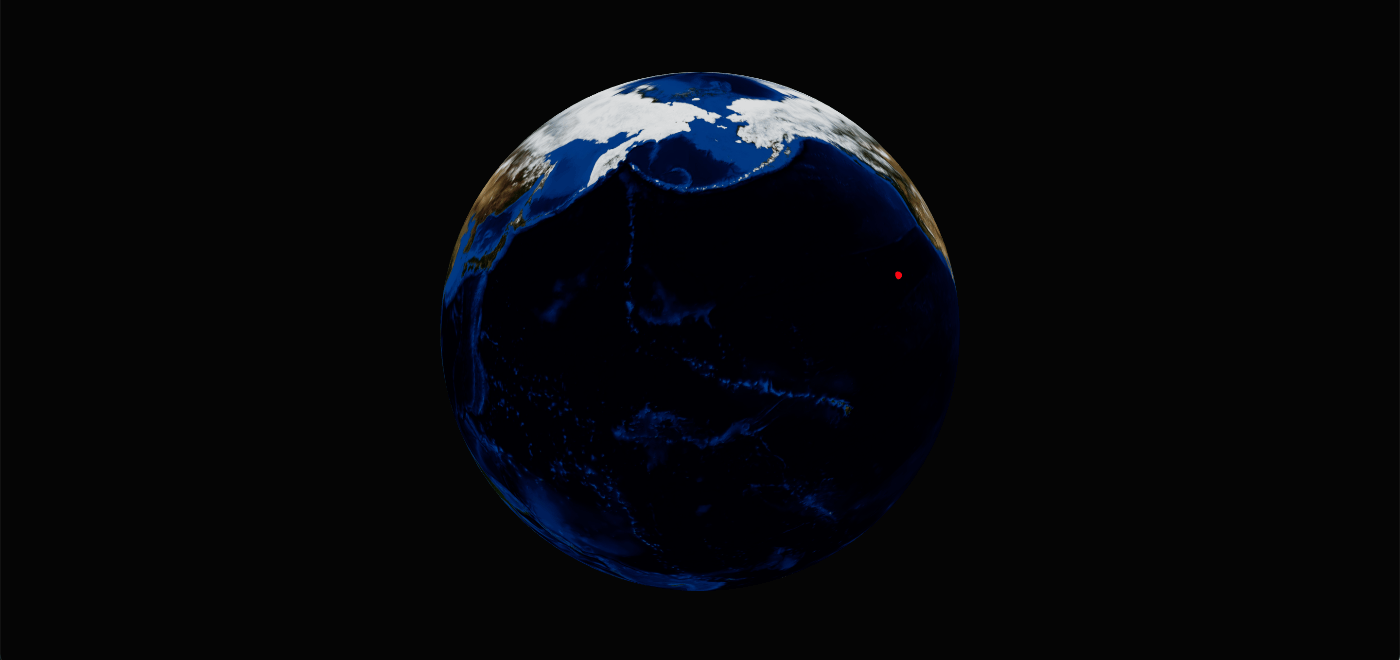
なんかおかしいです。
赤い点は羽田空港を指すはず。。
多少の誤差(数キロ)は許容するつもりでしたが、誤差どころかめちゃズレてる。
検証してみる
さて、それぞれの点の分布を調べるため、緯度、経度を6度ずつ等間隔に地球上に点を打ってみます。
const array: number[][] = [];
for(let lat = -15; lat < 15; lat++){
for(let lon = -30; lon < 30; lon++){
array.push([lat * 6,lon * 6]);
}
}
こんな感じで配列を作り、、、
{array.map((coord)=>(
<mesh position={getCoordinatesFromLatLon(coord[0],coord[1])}>
<sphereGeometry args={[1]}/>
<meshPhysicalMaterial />
</mesh>
))}
追加します。

うーん、変ですね。
中米のあたりが極になってしまっています。
どっちがどの軸かよくわからないので
<axesHelper args={[200]}/>
を追加して、軸のヘルパーを表示しました。

細くて見えにくいですが右側の黄色く見えるのがx軸、手前の青いのがy軸,最後に緑の線がz軸となっています。
上にある北極に点が集まってくるのが正しいと思うので、
function getCoordinatesFromLatLon(lat: number, lon: number): Vector3{
//ラジアンに変換
const φ = lat * Math.PI / 180;
const λ = lon * Math.PI / 180;
//地球の半径は今回100で設定したので
const r = 100;
//扁平率
const f = 1.0 / 298.257222101;
//第一離心率
const e = Math.sqrt( 2 * f - f * f );
const e2 = e * e;
const sini = Math.sin(φ);
const W = Math.sqrt( 1 - e2 * sini * sini);
//卯酉線曲率半径
const N = r / W;
const x = N * Math.cos(φ) * Math.cos(λ);
const y = N * Math.cos(φ) * Math.sin(λ);
const z = N * (1 - e2) * Math.sin(φ);
+ return new Vector3(x, z, y);
}
返り値のzとyを入れ替えました。

うまくできました。

ですが、いまだに羽田空港を指すはずの赤い点は間違った場所にいます。
しかし、よくみてみると緯度はあっているように見えます。
さらに、太平洋の真ん中は日付変更線が通ります。これは経度180度の線なのでここを基準に反転しているのでは無いでしょうか。
function getCoordinatesFromLatLon(lat: number, lon: number): Vector3{
//ラジアンに変換
const φ = lat * Math.PI / 180;
+ const λ = -1 * lon * Math.PI / 180;
//地球の半径は今回100で設定したので
const r = 100;
//扁平率
const f = 1.0 / 298.257222101;
//第一離心率
const e = Math.sqrt( 2 * f - f * f );
const e2 = e * e;
const sini = Math.sin(φ);
const W = Math.sqrt( 1 - e2 * sini * sini);
//卯酉線曲率半径
const N = r / W;
const x = N * Math.cos(φ) * Math.cos(λ);
const y = N * Math.cos(φ) * Math.sin(λ);
const z = N * (1 - e2) * Math.sin(φ);
return new Vector3(x, z, y);
}
強引な気がしますが、引数で受け取った経度をラジアンに変換する際に−1をかけてやりました。
さて、どうなったのでしょうか。

素晴らしい!きちんと緯度、経度から地球上のある一点を導くことができました。
最初の何が悪かったのかは、私はよく理解できていませんが何とかなりました。
おそらくこういうところなのでしょうが数学を学んでいない私には少々難しかったため、意識の低い解決方法で乗り切りました。
完成系
function getCoordinatesFromLatLon(lat: number, lon: number): Vector3{
//ラジアンに変換
const φ = lat * Math.PI / 180;
const λ = -1 * lon * Math.PI / 180;
//地球の半径は今回100で設定したので
const r = 100;
//扁平率
const f = 1.0 / 298.257222101;
//第一離心率
const e = Math.sqrt( 2 * f - f * f );
const e2 = e * e;
const sini = Math.sin(φ);
const W = Math.sqrt( 1 - e2 * sini * sini);
//卯酉線曲率半径
const N = r / W;
const x = N * Math.cos(φ) * Math.cos(λ);
const y = N * Math.cos(φ) * Math.sin(λ);
const z = N * (1 - e2) * Math.sin(φ);
return new Vector3(x, z, y);
}
つづく
今回は緯度と経度から3dの三次元空間である一点の座標を求める関数を作りました。
次回は飛行機の通るルートを視覚化したいと思います。
Discussion