多腕バンディット問題を試す(ジャグラーに挑む)
はじめに
Voicyでデータチームに所属しているいしけんです。
業務では放送のレコメンドなどに注力しています。
自身の勉強を目的に多腕バンディット問題について学習をおこなったので、そのアウトプットができればと思い記事を執筆しています。
基本的にはありきたりな内容になるかと思いますが、読んでいただけると嬉しいです!!
多腕バンディットってなんぞ??
多腕バンディット問題についての説明の前に、次のような状況を考えてみます。
- あるカジノに3台のスロットマシンが置いてあります。
- 各マシンはあたり/ハズレのどちらかを出力する。
- あたる確率はマシンごとによって異なる。
- これらのマシンを100回プレイします。
- プレイするマシンは毎回変えてもよい。
この時にどのようにプレイするとあたりによる報酬を最大化できるでしょうか。
当たり前ですが、3台のうち最もあたる確率が高いマシンをプレイし続ければ報酬を最大化できそうです。
しかし、あたる確率はカジノが設定しているため、私たちはその確率を知ることはできません。
そこで「問題をどのようにプレイすると報酬を最大化できるか」から、「どうすればあたりの確率が高いマシンを知れるか」に移して考えていきます。
「どうすればあたりの確率が高いマシンを知れるか」ですが、これは実際にプレイして情報を集めていくしか方法はありません。例えば、各マシンをn回ずつプレイして、マシンのあたり具合を調べる。その後、あたりやすいマシンを残りの(100-3*n)回をプレイすれば報酬に期待ができそうです。
このとき
- nを小さくすると
- 集められる情報の量が少ないのであたるマシンの推定が難しそう
- 獲得した情報をもとにあたりそうなマシンをプレイする回数が多い
- nを大きくすると
- 集められる情報の量が多いのであたるマシンの推定ができそう
- 獲得した情報をもとに当たりそうなマシンをプレイする回数が少ない
あたりやすいマシンを探索する必要がある一方、探索結果の知識を利用した行動を行いたいというジレンマが起こります。つまり、探索(あたりやすいマシンを探す)と知識利用(あたりやすそうなマシンをプレイする)という関係はトレードオフの関係になります。
多腕バンディット問題とは上記のような「選択肢が多数ありそれぞれ異なる確率で報酬が得られるときに、報酬が得られる選択肢を探し報酬を最大化する」という問題になり、その解決方針は選択肢の探索と獲得した知識を利用して報酬を得るという2つの行動をバランスをとりながら行うことになります。この時、得た知識を利用して次の選択肢を決定する戦略を方策(policy)と呼びます。
方策(policy)
主要な3つの方策について簡単に取り上げていきます。
-
ε-greedy
- εの確率でランダムに選択, 1-εの確率でその時点で最良の選択を行う
-
Upper Confidence Bound (UCB)
- 当たり割合が高い選択肢, 探索が足りていない選択肢だとスコアが高くなる
- 探索回数が十分に大きくなると当たり割合の高さが重視される
-
\text{UCB}_i = \bar{X}_i + \sqrt{\frac{2 \log n}{n_i}} -
\text{UCB}_i i -
\bar{X}_i i -
n -
n_i i -
\sqrt{\frac{2 \log n}{n_i}}
-
-
Thompson Sampling
- 各選択肢の「その選択肢が期待値最大である確率」を確率分布として持ち、これを試行の度に更新していきます。各試行で、各選択肢の確率分布からサンプルをランダムに抽出し、最も高いサンプル値を示す選択肢を選びます。選択した選択肢から得られた報酬(成功や失敗)に基づいてその選択肢の確率分布を更新し、次回の選択に反映します。
シミュレーションしてみる
上記の方策でいくつかシミュレーションを行いたいと思います。
スロットマシンのクラス(Bandit)、プレイヤーのクラス、上記3つの方策のクラスをpythonで実装し、シミュレーションを行いました。(コードに間違いがあった場合はそっとご指摘いただけると幸いです。)
ε-greedyについてはε=0.1に設定して実行しました。
Banditクラス
class Bandit:
def __init__(self, p):
self.p = p
self.a = 1
self.b = 1
self.N = 0
def pull(self):
return np.random.random() < self.p
def sample(self):
return np.random.beta(self.a, self.b)
def update(self, x):
self.a += x
self.b += 1 - x
self.N += 1
ε-greedyクラス
class EpsilonGreedy:
def __init__(self, epsilon, n_bandits):
self.epsilon = epsilon
self.counts = [0]*n_bandits
self.values = [0.]*n_bandits
def select(self):
if sum(self.values) == 0:
return np.random.randint(len(self.counts))
if np.random.random() < self.epsilon:
return np.random.randint(len(self.counts))
else:
return np.argmax(self.values)
def update(self, choice, reward):
self.counts[choice] += 1
n = self.counts[choice]
value = self.values[choice]
new_value = ((n - 1) / float(n)) * value + (1 / float(n)) * reward
self.values[choice] = new_value
UpperConfidenceBoundクラス
class UpperConfidenceBound:
def __init__(self, n_bandits):
self.counts = [0]*n_bandits
self.values = [0.]*n_bandits
def select(self):
if sum(self.values) == 0:
return np.random.randint(len(self.counts))
n = sum(self.counts)
ucb_values = [0.0]*len(self.counts)
for i in range(len(self.counts)):
if self.counts[i] == 0:
ucb_values[i] = float('inf')
else:
bonus = np.sqrt((2*np.log(n)) / self.counts[i])
ucb_values[i] = self.values[i] + bonus
return np.argmax(ucb_values)
def update(self, choice, reward):
self.counts[choice] += 1
n = self.counts[choice]
value = self.values[choice]
new_value = ((n - 1) / float(n)) * value + (1 / float(n)) * reward
self.values[choice] = new_value
ThompsonSamplingクラス
class ThompsonSampling:
def __init__(self, n_bandits):
self.bandits = [Bandit(0.5) for _ in range(n_bandits)]
def select(self):
samples = [b.sample() for b in self.bandits]
return np.argmax(samples)
def update(self, choice, x):
self.bandits[choice].update(x)
Playerクラス
class Player:
def __init__(self, bandits, strategy):
self.bandits = bandits
self.strategy = strategy
self.total_reward = 0
self.record = []
self.rates = []
self.choices = [0]*len(bandits)
def select_bandit(self):
choice_bndit = self.strategy.select()
self.choices[choice_bndit] += 1
return choice_bndit
def update(self, choice, reward):
self.strategy.update(choice, reward)
self.total_reward += reward
self.record.append(self.total_reward)
self.rates.append(self.total_reward / len(self.record))
シミュレーション1
設定
- あたり確率が0.3, 0.5, 0.9のマシンが1台ずつ存在
- 1000回プレイするシミュレーションを100回行う
結果

横軸はプレイ回数、縦軸はプレイ回数時点での報酬獲得割合の平均、赤の線は最も当たり確率の高いマシンの確率を表しています。
結果を見ると、どの方策でも最も当たり確率の高いマシンの確率である0.9に近づいており、報酬が最大になるようにマシンをプレイしている様子が確認できます。
Thompson samplingが最もうまく報酬を獲得できている、800回あたりでUCBがε-greedyを上回っているといった様子が確認できます。
シミュレーション2
設定
- あたり確立が0.05, 0.1 ,0.2, 0.25, 0.15, 0.3, 0.45, 0.35, 0.4, 0.5のマシンが1台ずつ存在
- 50000回プレイするシミュレーションを100回行う
結果

こちらも同様にどの方策でも報酬が最大になるようにマシンをプレイしている、Thompson samplingが最もうまく報酬を獲得できている、25000回あたりでUCBがε-greedyを上回っているという様子が確認できます。
まとめ
- 今回のシミュレーションでは全ての方策について、方策を最大化するようにプレイしている様子が確認できました。
- 途中でUCBがε-greedyを上回っている点について、UCBは未探索の選択肢を積極的に選択して情報を集め、十分探索すると当たる割合の高い選択肢を選ぶようになる、一方でε-greedyはずっとεの確率で探索を行う。従って長期的な報酬はUCBの方が高くなるためであると考えられる。
おまけ
シミュレーション3(ジャグラーに挑む)
ここらで少し遊びたくなったので、実際のスロットマシンにバンディットアルゴリズムで挑んでみようと思います。
今回は株式会社北電子が開発しているジャグラーシリーズのゴーゴージャグラー3を対象にします。ゴーゴージャグラー3の詳細はこちら。リンク先の確率表のBB確率とRB確率の合成確率を各台のあたり確率と設定します(要するにGOGOランプがペかる確率)。
設定
- 設定1~6までのゴーゴージャグラー3が1台ずつ存在
- 設定1~6までの各合成確率は1/149.6, 1/145.3, 1/139.7, 1/130.5, 1/123.7, 1/117.4
- 50000回プレイするシミュレーションを100回行う
結果
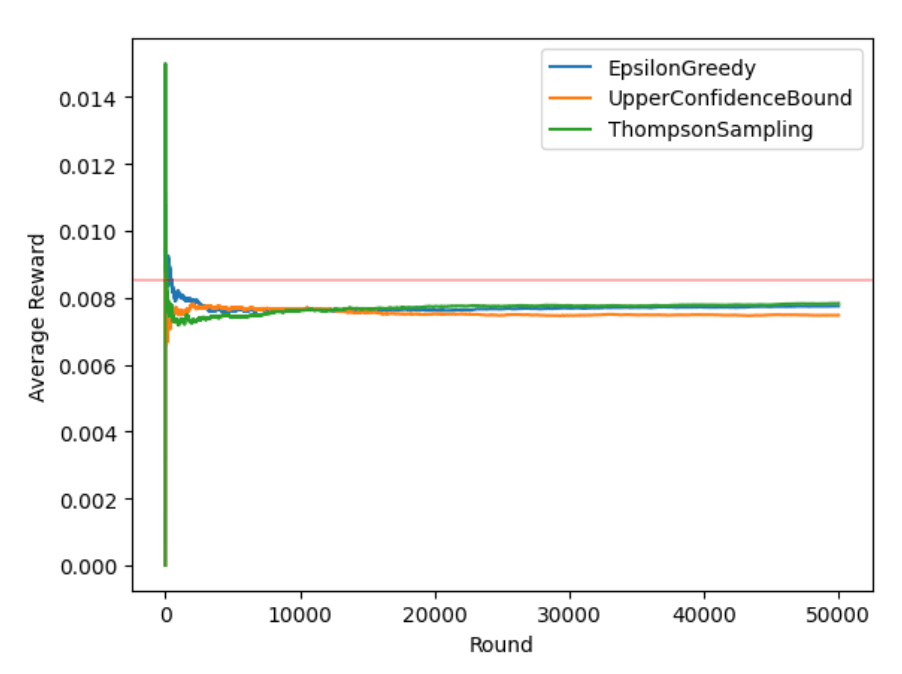
。。。渋いです
どの方策でも赤線(あたり確率が最も高い台のあたり確率)に近づけていないことより、あたり確率が高い台の推定がうまく行えていないようです。最も高いあたり確率であっても0.009以下であるため、そもそもあたりが引けずあたりやすい台を推定できるほどの情報が今回の試行回数では集まらなかったことが原因ではないかと考えています。
結論:ギャンブルはほどほどにしましょう!!
終わりに
今回はバンディット問題について取り上げ、基本的なシミュレーションを行いました。今後はバンディット問題の拡張である文脈付きバンディット問題の学習などについても学習できればと考えています。
コメントやいいねなどいただけると励みになります!!
Discussion