Zenn
📈

インクリメンタルに複数の時系列データに対する平均・標準偏差を計算する

2022/12/31に公開
4件
Python
Rust
統計
数値計算
tech

はじめに

データ分析を行う際、それらのデータの特徴を知るために頻繁に平均や分散（データのばらつき）を計算します。
それらは、n個のデータをx_1,x_2,\ldots,x_nと表すと、それぞれ次のような式で計算できました。

  • 平均
m_n = \frac{1}{n}\sum_{i=1}^{n}x_i
  • 分散
\sigma_{n}^2 = \frac{1}{n}\sum_{i=1}^{n} (x_i - m_n)^2

この計算式を愚直にコード(rust)に落とし込むと次のように記述できます。（もしrustを書いたことない方でもプログラミングに馴染みのある方であればなんとなくわかると思います。）

// 平均
fn mean(data: &Vec<f64>) -> f64 {
    let mut sum: f64 = 0.0;
    for i in 0..data.len() {
        sum += data[i];
    }
    sum / data.len()
}

// 分散
fn variance(data: &Vec<f64>, mean: f64) -> f64 {
    let mut sum: f64 = 0.0;
    for i in 0..data.len() {
        let diff = data[i] - mean;
        sum += diff * diff;
    }
    sum / data.len()
}

しかしながら、上記の実装には下記のような2つの大きな問題点があります。

  1. 足し合わせたデータを保持する変数sumは一般に大きな値となるため足し合わせられるデータdata[i]やdiffに対して、数値の桁数の差が大きい場合に丸め誤差の影響が大きくなる。
  2. データ配列に新しくデータが追加されたとき、全てのデータ保持しておかないと計算ができない。

つまり、上記の実装は結果に誤差が大きく含まれていたり、メモリ効率が悪いという問題点を抱えています。
しかし、この問題はカハンの加算アルゴリズムとWelfordのオンラインアルゴリズムを併用することで解決されます。
このアルゴリズムの紹介が本記事の1つ目の大きな目的です。

しかし、このアルゴリズムの紹介は他記事ですでに取り上げられているため、本記事では、このアルゴリズムの実用例として、複数の時系列データに対する平均・標準偏差の計算（専門的に言えば、時間に対しデータ同士が独立と仮定した場合のガウス過程回帰？）を行います。
具体的には下記の画像ような計算を行います。


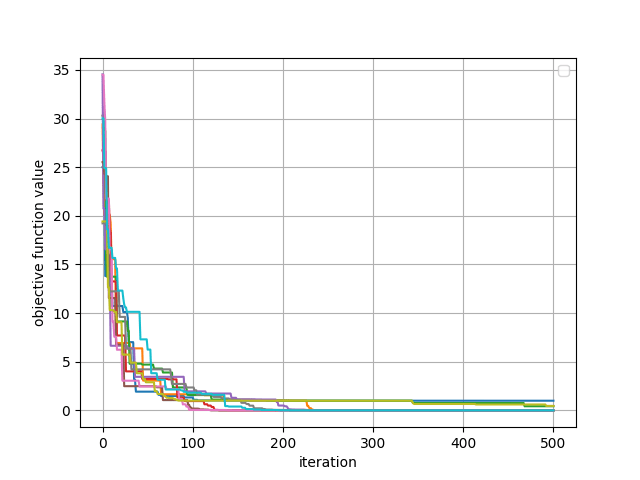
複数の時系列データ


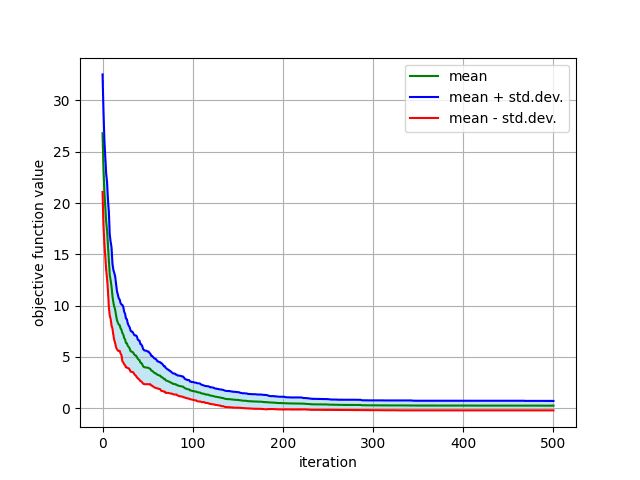
複数の時系列データに対する平均と標準偏差

本記事の目的

改めて本記事の目的について述べます。

  1. Welfordのオンラインアルゴリズムの紹介とその実装
  2. Welfordのオンラインアルゴリズム + カハンの加算アルゴリズムの応用として、複数の時系列データに対する平均・標準偏差の計算

Welfordのオンラインアルゴリズム

理論

このアルゴリズムはx_iに対して、逐次的に平均値及び分散の計算を行うことのできるアルゴリズムです。この方法は、計算の際に全てのデータを必要としないため、メモリ効率が良いという利点があります。
このアルゴリズムは下記のシンプルな更新則で構成されます。

  • 平均
m_n = m_{n-1} + \frac{x_n - m_{n-1}}{n}
平均の更新則の導出

Welfordのオンラインアルゴリズムにおける平均の更新則の導出を行う。
下記にデータ数がn, n-1の時のそれぞれの平均をm_n, m_{n-1}と表す。

m_{n} = \frac{1}{n} \sum_{i=1}^{n} x_i \\ m_{n-1} = \frac{1}{n-1} \sum_{i=1}^{n-1} x_i

ここで、m_{n}に注目し、下記のように式を変形する。

\begin{aligned} m_{n} &= \frac{1}{n} \sum_{i=1}^{n} x_i \\ &= \frac{n-1}{n} \cdot \frac{1}{n-1} \left ( \sum_{i=1}^{n-1} x_i + x_n \right ) \\ &= \frac{n-1}{n} \cdot \frac{1}{n-1} \sum_{i=1}^{n-1} x_i + \frac{n-1}{n} \cdot \frac{x_n}{n-1} \\ &= \frac{n-1}{n} m_{n-1} + \frac{x_n}{n} \\ &= \frac{(n-1)m_{n-1} + x_n}{n} \\ &= \frac{nm_{n-1} - m_{n-1} + x_n}{n} \\ &= m_{n-1} + \frac{x_n - m_{n-1}}{n} \end{aligned}
  • 分散
M_{2,n} = \sum_{i=1}^{n} (x_i - m_n)^2
M_{2,n} = M_{2,n-1} + (x_n - m_{n-1})(x_n - m_{n})
\sigma_n^2 = \frac{M_{2,n}}{n}
分散の更新則の導出

Welfordのオンラインアルゴリズムにおける分散の更新則の導出を行う。
下記にデータ数がn, n-1の時のそれぞれの平均を\sigma_n^2, \sigma_{n-1}^2と表す。

\sigma_{n}^2 = \frac{1}{n}\sum_{i=1}^{n} (x_i - m_n)^2 \\ \sigma_{n-1}^2 = \frac{1}{n-1}\sum_{i=1}^{n-1} (x_i - m_{n-1})^2

また、M_{2,n}, M_{2,n-1}をそれぞれ、

M_{2,n} = \sum_{i=1}^{n} (x_i - m_n)^2 = n \sigma_{n}^2 \\ M_{2,n-1} = \sum_{i=1}^{n-1} (x_i - m_{n-1})^2 = (n-1) \sigma_{n-1}^2

とおく。
ここで、M_{2,n}に注目し、式を下記のように変形する。

\begin{aligned} M_{2,n} &= \sum_{i=1}^{n} (x_i - m_n)^2 \\ &= \sum_{i=1}^{n} (x_i^2 - 2 m_n x_i + m_n^2) \\ &= \sum_{i=1}^{n} x_i^2 - \sum_{i=1}^{n} 2 m_n x_i + \sum_{i=1}^{n} m_n^2 \\ &= \sum_{i=1}^{n} x_i^2 - 2 m_n \sum_{i=1}^{n} x_i + n m_n^2 \\ &= \sum_{i=1}^{n} x_i^2 - \frac{2}{n} \sum_{i=1}^{n} x_i \cdot \sum_{i=1}^{n} x_i + n \cdot \left ( \frac{1}{n} \sum_{i=1}^{n} x_i \right )^2 \\ &= \sum_{i=1}^{n} x_i^2 - \frac{2}{n} \left ( \sum_{i=1}^{n} x_i \right )^2 + \frac{1}{n} \cdot \left ( \sum_{i=1}^{n} x_i \right )^2 \\ &= \sum_{i=1}^{n} x_i^2 - \frac{1}{n} \left ( \sum_{i=1}^{n} x_i \right )^2 \\ &= \sum_{i=1}^{n} x_i^2 - \cdot \frac{n-1}{n-1} \cdot \frac{1}{n} \left ( \sum_{i=1}^{n} x_i \right )^2 \\ &= \sum_{i=1}^{n} x_i^2 - \cdot \frac{n-1}{n-1} \left ( \sum_{i=1}^{n-1} x_i + x_n \right ) \cdot \frac{1}{n} \sum_{i=1}^{n} x_i \\ &= \sum_{i=1}^{n} x_i^2 - (n-1)m_{n-1} m_n - x_n m_n \\ &= \sum_{i=1}^{n} x_i^2 - n m_{n-1} m_n - x_n m_n + m_{n-1} m_n \\ &= \sum_{i=1}^{n-1} x_i^2 - n m_{n-1} m_n + x_n^2 - x_n m_n + m_{n-1} m_n * * * (A) \end{aligned}

同様にして、M_{2,n-1}も式変形を行う。

\begin{aligned} M_{2,n-1} &= \sum_{i=1}^{n-1} (x_i - m_{n-1})^2 \\ &= \sum_{i=1}^{n-1} (x_i^2 - 2 m_{n-1} x_i + m_{n-1}^2) \\ &= \sum_{i=1}^{n-1} x_i^2 - \sum_{i=1}^{n-1} 2 m_{n-1} x_i + \sum_{i=1}^{n-1} m_{n-1}^2 \\ &= \sum_{i=1}^{n-1} x_i^2 - 2 m_{n-1} \sum_{i=1}^{n-1} x_i + (n-1) m_{n-1}^2 \\ &= \sum_{i=1}^{n-1} x_i^2 - \frac{2}{n-1} \sum_{i=1}^{n-1} x_i \cdot \sum_{i=1}^{n-1} x_i + (n-1) \cdot \left ( \frac{1}{n-1} \sum_{i=1}^{n-1} x_i \right )^2 \\ &= \sum_{i=1}^{n-1} x_i^2 - \frac{2}{n-1} \left ( \sum_{i=1}^{n-1} x_i \right )^2 + \frac{1}{n-1} \cdot \left ( \sum_{i=1}^{n-1} x_i \right )^2 \\ &= \sum_{i=1}^{n-1} x_i^2 - \frac{1}{n-1} \left ( \sum_{i=1}^{n-1} x_i \right )^2 \\ &= \sum_{i=1}^{n-1} x_i^2 - \frac{n}{n} \sum_{i=1}^{n-1} x_i \cdot \frac{1}{n-1} \sum_{i=1}^{n-1} x_i \\ &= \sum_{i=1}^{n-1} x_i^2 - \frac{n}{n} \sum_{i=1}^{n-1} x_i m_{n-1} \end{aligned}

M_{2,n-1}の両辺からx_n m_{n-1}を引くと、

\begin{aligned} M_{2,n-1} - x_n m_{n-1} &= \sum_{i=1}^{n-1} x_i^2 - \frac{n}{n} \sum_{i=1}^{n-1} x_i m_{n-1} - x_n m_{n-1} \\ &= \sum_{i=1}^{n-1} x_i^2 - \frac{n}{n} \sum_{i=1}^{n} x_i m_{n-1} \\ &= \sum_{i=1}^{n-1} x_i^2 - n m_{n} m_{n-1} * * * (B) \end{aligned}

ここで、(A)に(B)を代入する。

\begin{aligned} M_{2,n} &= M_{2,n-1} - x_n m_{n-1} + x_n^2 - x_n m_n + m_{n-1} m_n \\ &= M_{2,n-1} + (x_n - m_{n})(x_n - m_{n-1}) \end{aligned}
  • 不偏分散
s_n^2 = \frac{M_{2,n}}{n-1}

※s_n^2は正規分布の分散を推定する際に使用する。

https://en.wikipedia.org/wiki/Algorithms_for_calculating_variance#Online_algorithm

しかし、このアルゴリズムのみでは、先述した2.の問題しか解決していません。
このため、1.の問題を解決するために更新則の第1項と第2項の足し合わせに対して、カハンの加算アルゴリズムを導入します。
これにより丸め誤差についても、軽減できるようになります。
カハンの加算アルゴリズムの詳細についてはこちらをご参照下さい。

実装

上記の手続きを、rustで実装すると下記のようなコードになります。
実装上の工夫としては、標準偏差の計算結果をキャッシュしている点です。
その理由として、標準偏差は分散の平方根として求めることができますが、一般にsqrt()の処理は反復計算となるため重い処理となります。
一方で、標準偏差はupper()やlower()（上側・下側の1シグマの計算）で複数仮呼び出しが行われることが予想されるため、この部分がボトルネックとなります。
このため、処理負荷を低減を行うためキャッシュ化を行っています。

#[derive(Clone)]
pub struct IncrementalStatistics {
    mean: f64, // 平均(式中のm_n)
    count: usize, //　データ数(式中のn)
    m_2: f64, // 分散を計算するための中間変数(式中のM_{2,n})
    c_mean: f64, // カハンの加算アルゴリズムにおけるmeanの補正項 
    c_m_2: f64, // カハンの加算アルゴリズムにおけるm_2の補正項 
    cached_standard_deviation: f64, // 標準偏差のキャッシュ
    cached_un_standard_deviation: f64, // 不偏分散に基づく標準偏差のキャッシュ
    is_cached_standard_deviation: bool, // 標準偏差のキャッシュがあるか？のフラグ
    is_cached_un_standard_deviation: bool, // 不偏分散に基づく標準偏差のキャッシュがあるか？のフラグ
}

impl IncrementalStatistics {

    // コンストラクタ
    pub fn new() -> IncrementalStatistics {
        IncrementalStatistics {
            mean: 0.0,
            count: 0,
            m_2: 0.0,
            c_mean: 0.0,
            c_m_2: 0.0,
            cached_standard_deviation: 0.0,
            cached_un_standard_deviation: 0.0,
            is_cached_standard_deviation: false,
            is_cached_un_standard_deviation: false,
        }
    }

    // 平均を返す
    pub fn mean(&self) -> f64 {
        self.mean
    }
    
    // 合計を返す
    pub fn sum(&self) -> f64 {
        self.mean * self.count as f64
    }

    // 分散を返す
    pub fn variance(&self) -> f64 {
        if self.count != 0usize {
            self.m_2 / self.count as f64
        } else {
            0.0f64
        }
    }

    // 不偏分散を返す
    pub fn un_variance(&self) -> f64 {
        if self.count > 1usize {
            self.m_2 / (self.count - 1) as f64
        } else {
            0.0f64
        }
    }

    // 標準偏差を返す（一度呼び出しを行った場合はキャッシュした結果を返す）
    pub fn standard_deviation(&mut self) -> f64 {
        if self.is_cached_standard_deviation {
            return self.cached_standard_deviation;
        }
        self.cached_standard_deviation = self.variance().sqrt();
        self.is_cached_standard_deviation = true;
        self.cached_standard_deviation
    }

    //  不偏分散に基づく標準偏差を返す（一度呼び出しを行った場合はキャッシュした結果を返す）
    pub fn un_standard_deviation(&mut self) -> f64 {
        if self.is_cached_un_standard_deviation {
            return self.cached_un_standard_deviation;
        }
        self.cached_un_standard_deviation = self.un_variance().sqrt();
        self.is_cached_un_standard_deviation = true;
        self.cached_un_standard_deviation
    }

    // 平均値 + 標準偏差を返す（上側の1シグマを返す）
    pub fn upper(&mut self) -> f64 {
        self.mean() + self.standard_deviation()
    }

    // 平均値 - 標準偏差を返す（下側の1シグマを返す）
    pub fn lower(&mut self) -> f64 {
        self.mean() - self.standard_deviation()
    }
    
    // 平均値 + 不偏分散に基づく標準偏差を返す（上側の1シグマを返す）
    pub fn un_upper(&mut self) -> f64 {
        self.mean() + self.un_standard_deviation()
    }

    // 平均値 - 不偏分散に基づく標準偏差を返す（下側の1シグマを返す）
    pub fn un_lower(&mut self) -> f64 {
        self.mean() - self.un_standard_deviation()
    }

    // 現在のデータ数を返す
    pub fn count(&self) -> usize {
        self.count
    }

    // Welfordのオンラインアルゴリズム + カハンの加算アルゴリズム
    // 引数dataは新たに追加されるデータ
    pub fn add(&mut self, data: f64) {
        self.count += 1;
        let delta: f64 = data - self.mean;
        IncrementalStatistics::kahan(delta / self.count as f64, &mut self.mean, &mut self.c_mean);
        let delta_2: f64 = data - self.mean;
        IncrementalStatistics::kahan(delta * delta_2, &mut self.m_2, &mut self.c_m_2);
        self.is_cached_standard_deviation = false;
        self.is_cached_un_standard_deviation = false;
    }

    pub fn add_bulk(&mut self, data_bulk: &Vec<f64>) {
        for i in data_bulk {
            self.add(*i);
        }
    }

    // メンバの初期化
    pub fn clear(&mut self) {
        self.mean = 0.0;
        self.count = 0;
        self.m_2 = 0.0;
        self.c_mean = 0.0;
        self.c_m_2 = 0.0;
        self.cached_standard_deviation = 0.0;
        self.cached_un_standard_deviation = 0.0;
        self.is_cached_standard_deviation = false;
        self.is_cached_un_standard_deviation = false;
    }

    // カハンの加算アルゴリズム
    fn kahan(data: f64, sum: &mut f64, c: &mut f64) {
        let y: f64 = data - *c;
        let t: f64 = *sum + y;
        *c = (t - *sum) - y;
        *sum = t;
    }
}

https://github.com/utcarnivaldayo/incremental_statistics

複数の時系列データに対する平均・標準偏差を求める

Welfordのオンラインアルゴリズムの実用例として、複数の時系列データに対する平均・標準偏差の計算を行います。
この計算を行うことの利点として、下記画像のように時系列データが多数存在し、グラフが見づらいケースにおいてそれらの平均・標準偏差を算出することでその特徴を捉えやすくすることができます。


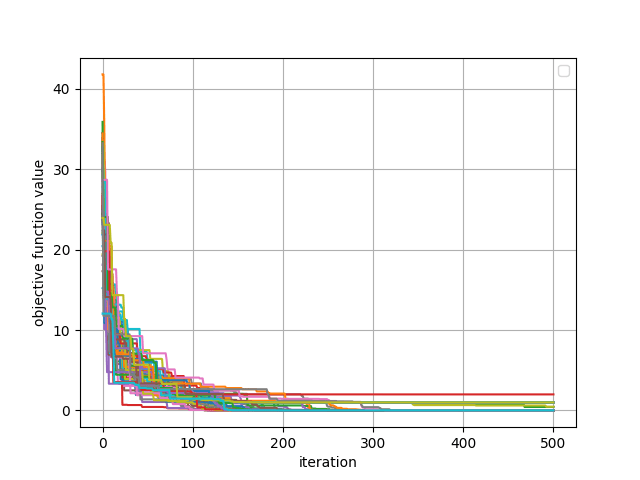
50個の時系列データ

しかしながら、この計算を行う際に注意しなければいけない点として、時系列データの平均・標準偏差を愚直に計算する場合では、時系列データ数 x 時系列データ長の非常に大きいメモリ領域を使用します。
このとき、時系列データを1サンプルずつで平均・標準偏差の計算するとメモリを節約して計算することができますが、1サンプル毎にに対して時系列データ数分のファイルの入出力が発生するため、オーバーヘッドが大きくなってしまいます。
ここで有効になってくるのが、Welfordのオンラインアルゴリズムです。この方法であれば、1つずつ時系列データを読み込んで処理できるためファイルIOのオーバヘッドも少なく、メモリ領域も時系列データ1つ分で平均・標準偏差の計算を逐次的に行うことができます。

use ::series_statistics_csv::series_statistics_csv::SeriesStatisticsCsv;
use series_statistics::series_statistics;

fn main() {
    let trial: usize = 50; // 時系列データの数
    let length: usize = 501; // データ長

    // SeriesStatistics は IncrementalStatisticsオブジェクトを配列化したもの
    let mut inc_series = series_statistics::SeriesStatistics::new(length);

    // 複数の時系列データのファイルの読み込み
    for i in 0..trial {
        let mut data = Vec::new();
        let file_path: String = "/Users/xxxxxxxx/Desktop/workspace/"
            .to_string()
            + &i.to_string()
            + &"/series.csv".to_string();
        let mut reader = csv::ReaderBuilder::new()
            .has_headers(true)
            .from_path(file_path);

        for record_result in reader.unwrap().records() {
            let record = record_result.unwrap();
            data.push(record[1].parse::<f64>().unwrap());
        }

        // インクリメンタルに統計量を計算
        inc_series.add(&data);
    }

    // 横軸データ
    let x = (0..length).map(|n| n as f64).collect::<Vec<f64>>();

    // pandasのフォーマットでファイルを書き出す
    inc_series.write(
        "/Users/xxxxxxxx/Desktop/workspace/statistics.csv".to_string(),
        &x,
        "iteration".to_string(),
        "mean".to_string(),
        "std.dev.".to_string(),
        "upper".to_string(),
        "lower".to_string(),
    );
}

ここで、使用したseries_statistics及びseries_statistics_csvクレートはgithub上で公開しています。
https://github.com/utcarnivaldayo/series_statistics
https://github.com/utcarnivaldayo/series_statistics_csv

出力されたstatistics.csvファイルからmatplotlibを利用しグラフ化を行います。

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

# statistics.csvファイルの読み込み
filepath = 'statistics.csv'
df = pd.read_csv(filepath, sep=',', index_col=0)
time=np.array(list(df['iteration']))
upper=np.array(list(df['upper']))
lower=np.array(list(df['lower']))
mean=np.array(list(df['mean']))
print(df)

# グラフの描画
alpha=0.5
label_name_x = 'iteration'
label_name_y = 'objective function value'
plt.xlabel(label_name_x, rotation='horizontal')
plt.ylabel(label_name_y, rotation='vertical')
plt.plot(time, mean, color='green', label='mean')
plt.plot(time, upper, color='blue', label='mean + std.dev.')
plt.plot(time, lower, color='red', label='mean - std.dev.')
plt.grid()
plt.legend(loc='upper right')
plt.fill_between(time, upper, lower, label='sample', facecolor='skyblue', alpha=alpha, where=upper>lower)
plt.show()

かなり見やすくなりました。


複数の時系列データに対する平均と標準偏差

おわりに

本記事では、インクリメンタルに平均・分散を計算可能なWelfordのオンラインアルゴリズムについて説明を行い、その応用例として複数時系列データに対する平均・標準偏差の計算を行いました。
今回の応用例は複数の試行実験を行う最適化（メタヒューリスティクス・進化計算）や機械学習の誤差関数の推移曲線（更新曲線）に使用すれば最適化・学習アルゴリズムの収束や停滞の様子を統計的に見ることができるとのではと考えています。また、この方法はリアルタイムに追加されるデータなどにも対応できるため活用方法を今後も考えていきたいと思います。

参考記事

https://qiita.com/Ushio/items/f5630d87f55c7afa984e

https://en.wikipedia.org/wiki/Algorithms_for_calculating_variance#Online_algorithm

Discussion

takotakottakotakot

Welfordのオンラインアルゴリズムにおける分散の更新則の導出を行う。

の2番目の数式の m_n は m_{n-1} の打ち間違えでしょうか。次の M_{2,n−1} の方は合っていました。
​

utut

ご指摘頂きありがとうございます!
修正致しました。

catatsuycatatsuy

素敵な記事をありがとうございます。間違いではないかと思った箇所があったので指摘します。

「分散の更新則の導出」のB式の導出ですが、全4式の中の間の2式がおかしいと思います。最初の式と最後の式の2式だけで良いのではないでしょうか？

utut

「分散の更新則の導出」のB式の導出ですが、全4式の中の間の2式がおかしいと思います。

ご指摘頂きありがとうございます！2式目は誤りでしたので削除させて頂きました。

最初の式と最後の式の2式だけで良いのではないでしょうか？

途中式は総和部分がnサンプルの平均になっていることを明示的に示したかったので、残させて頂きました。