Julia入門者がJuliaで微分方程式を解いてみる

最近 Julia に入門し始めました。これはその記念記事?です。

(古典的)Runge-Kutta法

微分方程式を解くアルゴリズムはいくつかありますが、今回は古典的Runge-Kutta法を取り上げます。（最も使われている数値解法らしい）
Runge-Kutta法は常微分方程式を数値的に解く方法の一種です。ルンゲ-クッタ法の中でもいくつか分類されるようですが詳細については素人の僕が説明するよりかは良書や良記事がすでにあるのでそちらで調べた方が良いでしょう。

古典的Runge-Kutta法は以下の計算式に示されるもので、この計算式で微分方程式$\dot{x}(t)=f(t,x)$の近似解を得ることが出来ます。

$$\begin{align} x_0 &= x(t_0) \\ k_1 & = f(t_n, x_n) \\ k_2 & = f(t_n+\frac{h}{2}, x_n+\frac{h}{2}k_1) \\ k_3 & = f(t_n+\frac{h}{2}, x_n+\frac{h}{2}k_2) \\ k_4 & = f(t_n+h, x_n+hk_3) \\ x_{n+1} &= x_n + \frac{h}{6}(k_1+2k_2+2k_3+k_4) \end{align}$$

ここで$h$はきざみ幅で小さめの値をとります。

これを julia で実装すると次のようなコードになります。

function runge_kutta(f, 𝒙₀, h, maxiter)
    trajectoryₓ = Array{Float32, size(𝒙₀, 1)}(undef, length(𝒙₀), maxiter)

    trajectoryₓ[:,1] = 𝒙₀

    𝒙ᵢ₋₁ = 𝒙₀
    for i in 2:maxiter
        kᵢ₁ = f(𝒙ᵢ₋₁)
        kᵢ₂ = f(𝒙ᵢ₋₁ + 0.5*h*kᵢ₁)
        kᵢ₃ = f(𝒙ᵢ₋₁ + 0.5*h*kᵢ₂)
        kᵢ₄ = f(𝒙ᵢ₋₁ + h*kᵢ₃)
        𝒙ᵢ = 𝒙ᵢ₋₁ + h*(kᵢ₁ + 2kᵢ₂ + 2kᵢ₃ + kᵢ₄)/6.0
        trajectoryₓ[:,i] = 𝒙ᵢ
        𝒙ᵢ₋₁ = 𝒙ᵢ
    end
    trajectoryₓ
end

Task1. 減衰系の自由振動

次の減衰系の自由振動の振る舞いを解いてみます。

質量: $1$
減衰係数: $2c$
バネ定数: $k$

運動方程式は次のようになります。

$$\ddot{x}+2c\dot{x}+kx=0$$

この方程式の一般解は次のようになります。

$$\begin{align} x &= A_1\exp(\lambda_1t) + A_2\exp(\lambda_2t) \\ \lambda_1, \lambda_2 &: -c \pm \sqrt{c^2-k} \\ A_1, A_2 &: 任意の定数 \end{align}$$

ここで

• $c^2-k>0$: 過減衰(overdumping)
• $c^2-k=0$: 臨界減衰(critical dumping)
• $c^2-k<0$: 不足減衰(underdumping)

となります。

また $x_1 = x$, $x_2=\dot{x}$ として1階の微分方程式にすると次のようになります。

$$\begin{align} \dot{x_1} &= x_2 \\ \dot{x_2} &= -2cx_2-kx_1 \end{align}$$

上で定義したrunge_kutta関数を使って過減衰、臨界減衰、不足減衰のそれぞれの振る舞いを見てみましょう。

using PyPlot

const OUTPUT_DIR = "output"

function generate_free_vibration_function(c, k)
    𝒙->[
        𝒙[2];
        -2c*𝒙[2]-k*𝒙[1]
        ]
end

overdumping  = runge_kutta(generate_free_vibration_function(1.5, 1.0), [0.1;0.3], 0.001, 18000)
critdumping  = runge_kutta(generate_free_vibration_function(1.0, 1.0), [0.1;0.3], 0.001, 18000)
underdumping = runge_kutta(generate_free_vibration_function(0.5, 1.0), [0.1;0.3], 0.001, 18000)

mkpath("$OUTPUT_DIR")

fig, axes = subplots(1, 2, figsize=(8,4))
axes[1].plot(overdumping[1,:], color="b", label="overdumping")
axes[1].plot(critdumping[1,:], color="g", label="critical dumping")
axes[1].plot(underdumping[1,:], color="r", label="underdumping")
axes[1].set_xlabel("t"), axes[1].set_ylabel("x")
axes[1].set_title("time-series")
axes[1].legend()

axes[2].plot(overdumping[1,:], overdumping[2,:], color="b", label="overdumping")
axes[2].plot(critdumping[1,:], overdumping[2,:], color="g", label="critical dumping")
axes[2].plot(underdumping[1,:], overdumping[2,:], color="r", label="underdumping")
axes[2].set_xlabel("t"), axes[2].set_ylabel("x")
axes[2].set_title("phase space")
axes[2].legend()

tight_layout()

fig.savefig("$OUTPUT_DIR/free_vibration.jpg")

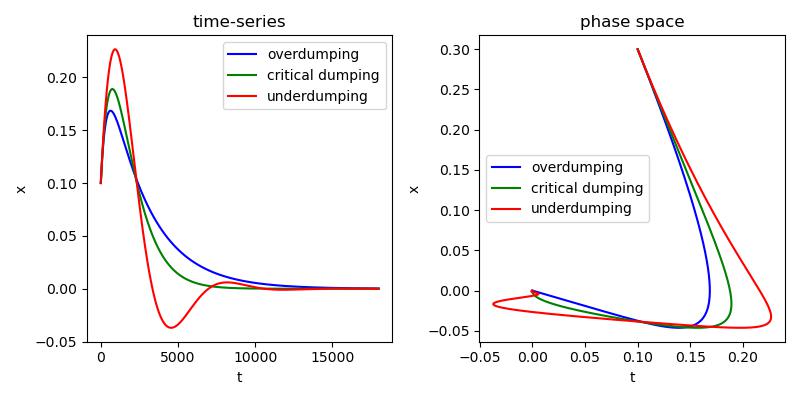
過減衰と臨界減衰では振動せずに減衰する一方で不足減衰では振動しながら減衰している様子がわかります。また、過減衰より臨界減衰の方が先に平衡位置へ収束される様子もみれますね。

Task2. ファン・デル・ポール振動子

オランダのvan der Pol博士によって提案された振動子でその支配方程式は次になります。

$$\ddot{x}-\epsilon(1-x^2)\dot{x}+x=0$$

この方程式はリミットサイクルが存在する非線形微分方程式として有名です。
減衰力の項の係数 $-\epsilon(1-x^2)$ が正の場合は振動が大きくなり（自励振動）に、いっぽうで負の値の場合は振動が小さくなります(減衰振動)。このバランスによって振動が持続する振る舞いになります。この持続する振動の起動をリミットサイクルと言います。

このファン・デル・ポール型の微分方程式を1階の微分方程式を $x_1 = x$, $x_2=\dot{x}$ として書き直すと次のようになります。

$$\begin{align} \dot{x_1} &= x_2 \\ \dot{x_2} &= \epsilon(1-x^2)\dot{x}-x \end{align}$$

ここでも runge_kutta関数を使って振る舞いを見てみましょう。初期値を $(x,\dot{x})=(0.1, 0.3)$と $(x,\dot{x})=(2.5, 5)$ の2パターンで、さらに$\epsilon$を$[0.1, 1.0, 10]$の3パターンで、合計6パターンで解いてみます。

using PyPlot
using DataStructures

const OUTPUT_DIR = "output"
mkpath("$OUTPUT_DIR")

const STEP_SIZE = 0.001
const TOTAL_STEP = 80000

initial_value = [[0.1;0.3], [2.5;5]]
parameters = [0.1, 1.0, 10.]

function generate_vanderPol_function(ϵ)
    𝒙->[
        𝒙[2];
        ϵ*(1-𝒙[1]^2)*𝒙[2]-𝒙[1]
        ]
end

solutions  = OrderedDict{Float64, Array{Array{Float64, 2}}}(
        ϵ => map(init->runge_kutta(generate_vanderPol_function(ϵ), init, STEP_SIZE, TOTAL_STEP), initial_value) 
        for ϵ in parameters )

display(keys(solutions))

fig, axes = subplots(3, 2, figsize=(12, 18))

plot_color = ["b", "r"]

for (i, (parameter, solution)) in enumerate(solutions)
    for initval_case in 1:2
        axes[i, 1].plot(solution[initval_case][1,:], color=plot_color[initval_case], label=initial_value[initval_case])
        axes[i, 1].set_xlabel("t"), axes[i, 1].set_ylabel("x")
        axes[i, 1].legend()
    
        axes[i, 2].plot(solution[initval_case][1,:], solution[initval_case][2,:], color=plot_color[initval_case], label=initial_value[initval_case])
        axes[i, 2].set_xlabel("x"), axes[i, 2].set_ylabel("dot(x)")
        axes[i, 2].legend()
    end
    ax_pos = axes[i, 1].get_position()
    xpos = ax_pos.x0 - 0.1
    ypos = 0.5 * (ax_pos.y0 + ax_pos.y1)
    fig.text(x=xpos, y=ypos, s=string("ϵ=",parameters[i]), size=18)
end

axes[1, 1].set_title("time-series", y=1.1, size=18)
axes[1, 2].set_title("phase space", y=1.1, size=18)

fig.savefig("$OUTPUT_DIR/vanderPol.jpg")

結果は次の図のようになります。

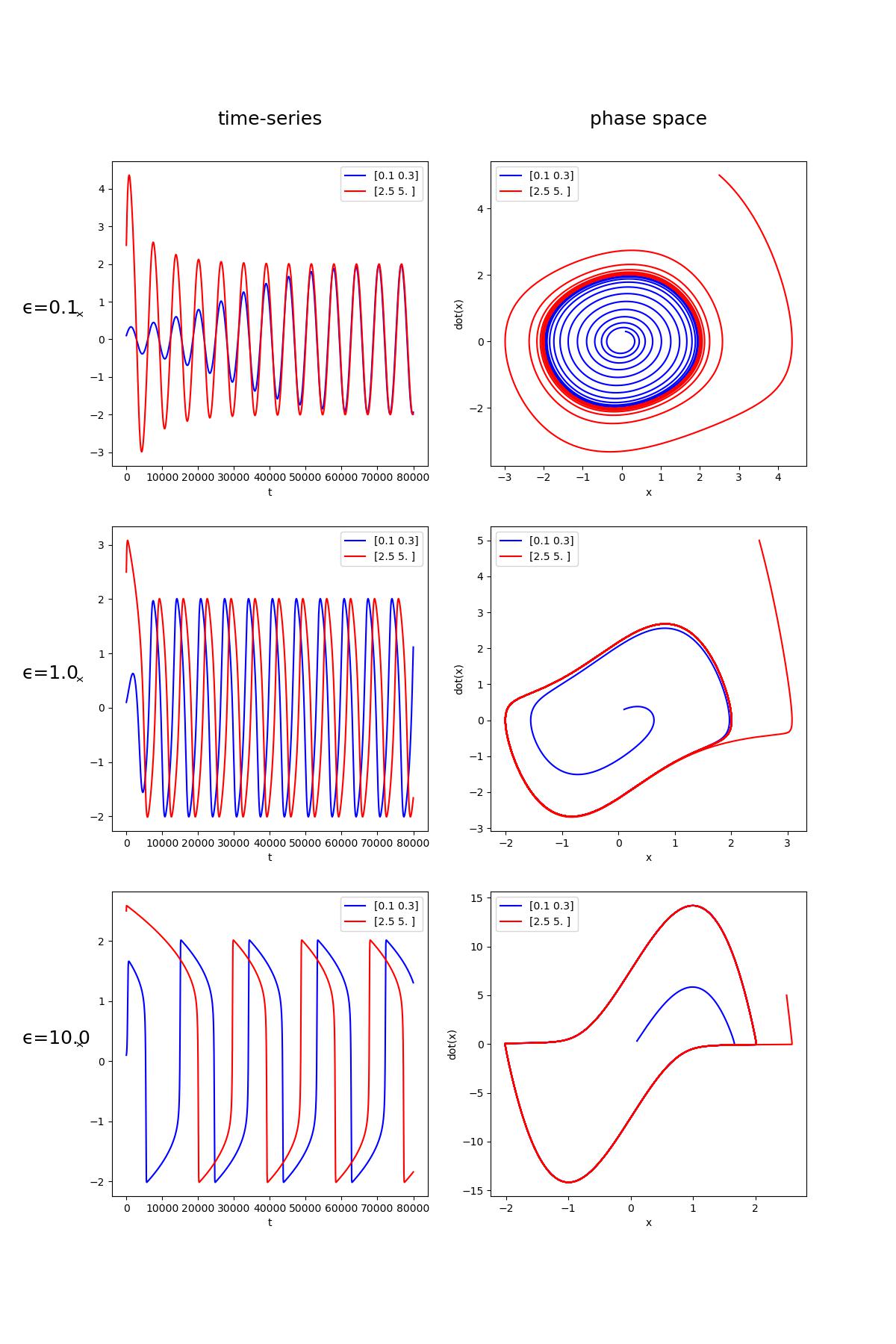
初期値は発生するリミットサイクルの内側と外側の2パターンで試しており、ともにリミットサイクルに収束されることが観測できます。さらに$\epsilon=0.1$の時は正弦波に近い形をしていますが、$\epsilon=10.0$の時はゆっくり動いた後に突然移動するような動きとなっています。このような運動は弛緩運動とよばれます。

参考文献

• 機械振動工学 (石田幸男・井上剛志 共著)
• Juliaで作って学ぶベイズ統計学 (須山敦志 著)