シェーダーで菱形が作れるのを言語化してみた

分からなかった事が分かったから記事にしといた

今回はシェーダーの事というよりかは数学的なお話が少しだけ入るかも
きっかけはなんで菱形って作れるんだろうという疑問から
ChatGPTと壁打ちしながら理解に至ったので書き記しておこうと思った次第。
まずChatGPTにGLSLでShaderToyで使える菱形のコーディングを書いてと言ったら出てきたのがこちら

hisigata

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    vec2 uv = fragCoord / iResolution.xy;
    
    // 座標を中心に移動
    uv = uv * 2.0 - 1.0;
    
    // アスペクト比を考慮したスケーリング
    uv.y *= iResolution.y / iResolution.x;
    
    // マンハッタン距離を計算
    float d = abs(uv.x) + abs(uv.y);
    
    // 距離が0.15以下であれば白色、そうでなければ黒色
    vec3 color = d <= 0.15 ? vec3(1.0) : vec3(0.0);
    
    fragColor = vec4(color,1.0);
}

自分が分かってなかったのは、このマンハッタン距離と
このコーディングから最終的な出力結果が結びついていなかったことです。

理解への至り方

まず、マンハッタン距離を調べました。
最初気づくのが遅れたのですが、原点Oから点がずれているところで理解が一気に進みました。
https://manabitimes.jp/math/1127
ここで、菱形の断片的な作り方は完全に理解しました。
ですが、一つの直角三角形しか自分の中では描画されていない状態でした。
自分のイメージでは以下のような画像のままでした。

では、絶対値はどういう役割をしているんだろうというのを考えることにしました。
考えること５分位
「あれ、そもそもこれって原点は中心か…ってことは普通にマイナスはありえる」
ここでもう大体の理解はしました。
第一象限から第四象限で同じ事が起きていただけという感じに理解しました。

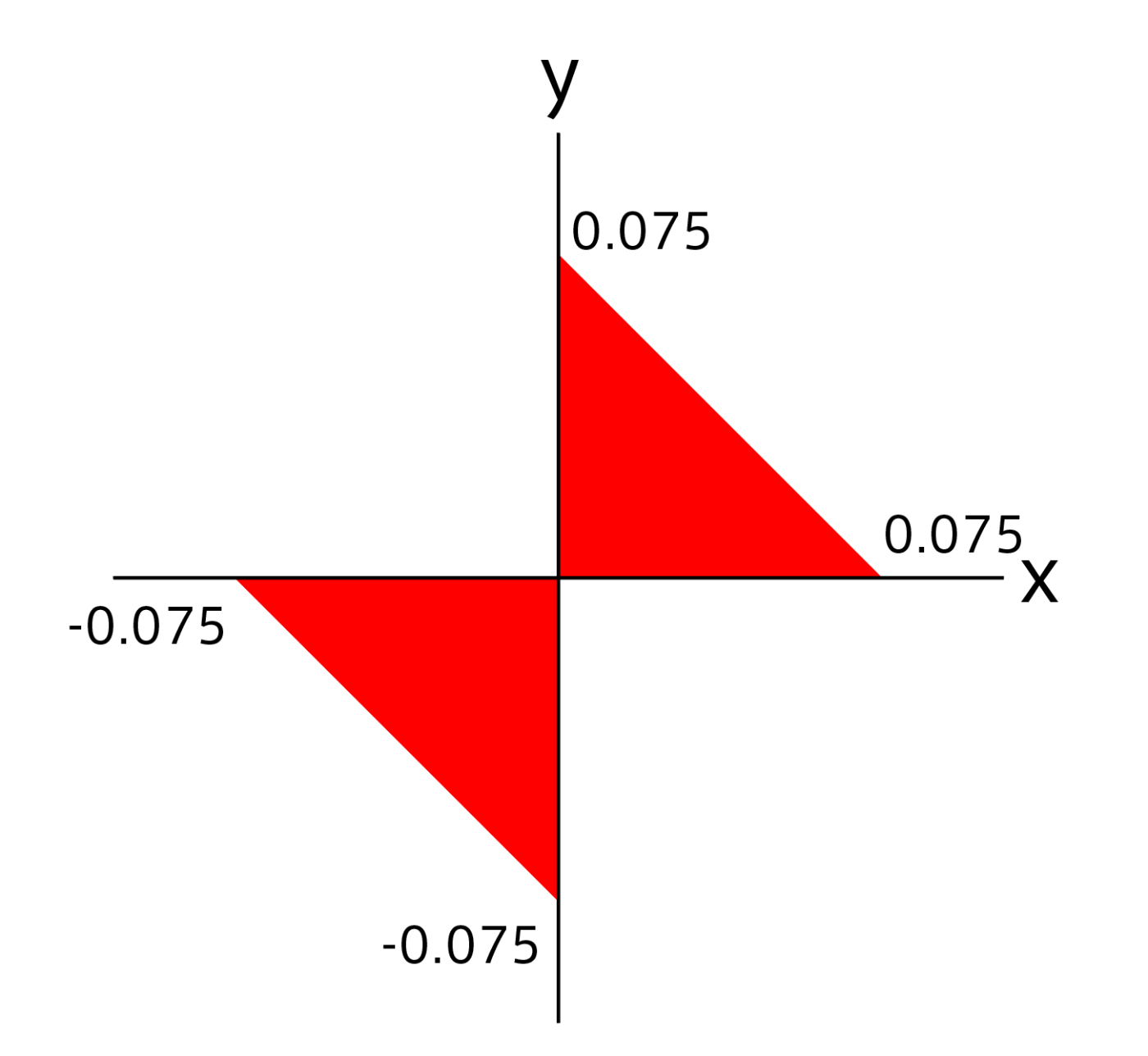
そのためには絶対値を使うのが楽なのだろうと思われる。

本当に絶対値いる？

疑り深いので実は無くても…って思いながら
絶対値抜きで書いてみました。

hisigata

void mainImage(out vec4 fragColor, in vec2 fragCoord) {
  vec2 uv = fragCoord / iResolution.xy;
  
  uv = uv * 2.0 - 1.0;
  
  uv.y *= iResolution.y / iResolution.x;
  
  float angle = radians(45.0);
  
  vec2 rotatedUV;
  rotatedUV.x = uv.x * cos(angle) - uv.y * sin(angle);
  rotatedUV.y = uv.x * sin(angle) + uv.y * cos(angle);
  
  vec3 color;
  if (rotatedUV.x >= -0.15 && rotatedUV.x <= 0.15 && rotatedUV.y >= -0.15 && rotatedUV.y <= 0.15) {
    color = vec3(1.0);
  } else {
    color = vec3(0.0);
  }
  
  fragColor = vec4(color, 1.0);
}

長い…そもそも出来上がったのは四角形でUVを回転させているので敗北感がすごい。
absを使ったほうがコードも短くとてもシンプルであることが理解できました。

数学楽しい

数学凄く苦手で、このシェーダーの勉強を始めたと同時に小学１年生から学び直していました。
今は高校２年あたりまで学習出来てます。特に平面座標や図形の話は今後自分がやりたいことと強く結びつきを感じたので楽しいです。このまま線形代数や幾何学も学んでいきたい。

また、この理解によりlength関数で円が作れるのもすぐ分かりました。
ユークリッド距離だから、それはそうか…という第二の気づきにまで繋がったので
原点Oを軸とした点Pがぐるっと回るんだもんな…って感じで
頭の中でコンパスが回るような映像が湧いた！

数学楽しい！