※この記事は数理最適化Advent Calender2020の6日目の記事です.5日目は@ikeday_jagaさんによる数理最適化モデリング言語 PySIMPLE の紹介でした.
はじめに
列生成法(column generation method)は線形計画問題に対する単体法のバリエーションの1つです.整数計画問題を解こうとすると,変数の数が膨大でそもそも線形計画緩和問題すら解けそうにない状況が少なくありません.列生成法はそのような状況において,全ての変数を陽に考慮することなく線形計画問題を解いてしまう手法です.列生成法は,GilmoreとGomoryによって1961年に提案されました.ここでは,その論文で取り上げられた資材切出し問題(cutting stock problem)を例に列生成法を紹介します.
資材切出し問題と定式化
資材切出し問題は,定型の母材から様々な長さの板材を顧客の注文に応じて切り出す計画問題で,鉄鋼・製紙・繊維などの素材産業をはじめとする多くの分野に応用を持つ代表的な組合せ最適化問題の一つとして知られています.素材産業では,歩留りの向上すなわち余剰素材の削減が最も重要な課題で,資材切出し問題では,使用する母材の本数を最小にする製品の取合せを求める問題として定式化します.
ある鉄鋼会社が,長さLの大きな板材(母材)を市場に提供しています.しかし,顧客の注文はもっと短い板材です.長さl_1,l_2,\dots,l_mの板材をそれぞれd_1,d_2,\dots,d_m本ずつ生産する必要が生じたときに,なるべく少ない本数の母材を用いて顧客の注文を全て満たす切出し計画を求める問題が資材切出し問題です.
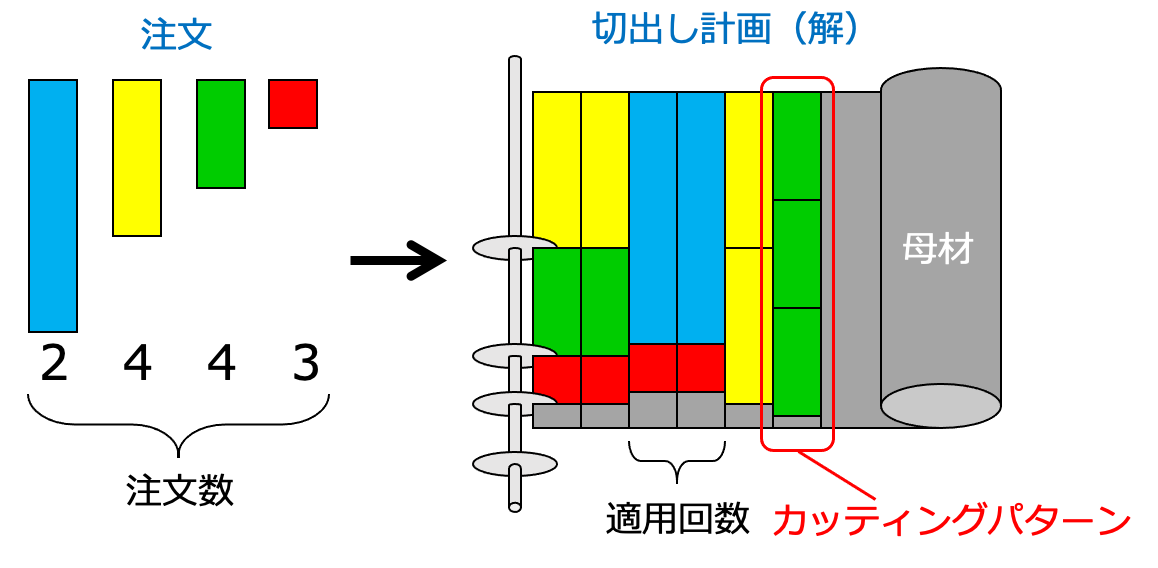
まず,カッティングパターン(以後,パターンと略します)と呼ばれる1枚の母材から切り出される短い板材の組合せを考えます.パターン\mathbf{p}_jに含まれる板材iの数をa_{ij}とすると,各パターン\mathbf{p}_j = (a_{1j},a_{2j},\dots,a_{mj})が満たすべき条件は以下の通りに書けます.
\sum_{i=1}^m a_{ij} l_i \le L.
例えば,長さL=70の母材から,長さl_1=17の板材3枚と長さl_2=15の板材1枚を切り出すパターンは\mathbf{p}=(3,1,0,\dots,0)と表せます.ここで,可能な全てのパターンを\mathbf{p}_1,\mathbf{p}_2,\dots,\mathbf{p}_nとし,変数x_jを各パターン\mathbf{p}_jの切出し回数とします.すると,資材切出し問題は以下の整数計画問題として定式化できます.
\begin{array}{lll}
\textnormal{最小化} & \displaystyle\sum_{j=1}^n x_j\\
\textnormal{条件} & \displaystyle\sum_{j=1}^n a_{ij} x_j \ge d_i, & i=1,\dots,m,\\
& x_j \in \mathbb{Z}_+, & j=1,\dots,n.
\end{array}
ここで,\mathbb{Z}_+は非負整数全体の集合を表します.
実際に解きたいのは整数計画問題ですが,各板材の注文数d_iがある程度大きければ,各パターンの切出し回数x_jの整数条件を緩和して得られる線形計画問題を解いて,得られた実数最適解を適当な方法で丸めることで,実用的には十分に質の高い解を求めることができます.しかし,板材の種類数mが比較的小さい場合でも,可能な全てのパターンの数nが膨大になるため,これらを列挙してから解いたのでは,効率的な線形計画ソルバーを用いても現実的な計算時間で解くことはできません.そこで,GilmoreとGomoryは可能な全てのパターンをあらかじめ列挙するのではなく,少数のパターンからなる実行可能解から始めて,現在の実行可能解を改善するパターンのみを逐次生成する列生成法を提案し,これを改訂単体法に組み込むことで,資材切出し問題(の線形計画緩和問題)が効率的に解けることを示しました.
双対問題と列生成法
初期実行可能解を見つけるのは簡単です.長さl_iの板材\lfloor L / l_i \rfloor本だけからなるパターンを\mathbf{p}_iと定めれば,パターン\mathbf{p}_1,\mathbf{p}_2,\dots,\mathbf{p}_mからなる行列は,線形計画問題に対する実行可能な基底行列になります.したがって,以降では,パターン\mathbf{p}_1,\mathbf{p}_2,\dots,\mathbf{p}_k (k \ge m)に対する線形計画問題の最適基底解が得られていると仮定して,そこに新たなパターン\mathbf{p}^{\prime} = (a_1^{\prime},a_2^{\prime},\dots,a_m^{\prime})を追加する場合を考えます.このとき,線形計画問題の双対問題は
\begin{array}{lll}
\textnormal{最大化} & \displaystyle\sum_{i=1}^m d_i y_i\\
\textnormal{条件} & \displaystyle\sum_{i=1}^m a_{ij} y_i \le 1, & j=1,\dots,k,\\
& y_i \ge 0, & i = 1,\dots,m.
\end{array}
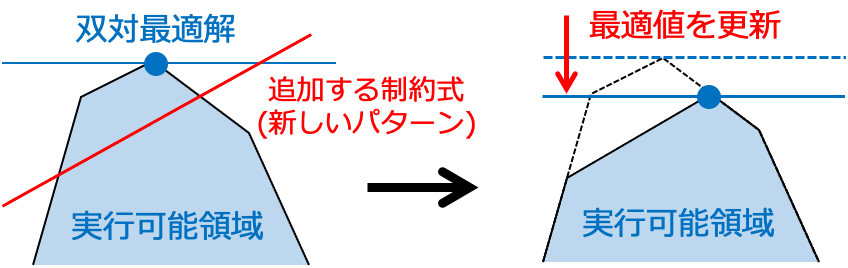
となり,パターン\mathbf{p}_1,\mathbf{p}_2,\dots,\mathbf{p}_kは1番目の制約条件に対応しています.この双対問題の最適解を\mathbf{y}^{\ast} = (y_1^{\ast},y_2^{\ast},\dots,y_m^{\ast})とすると,下図に示すように,\sum_{i=1}^m y_i^{\ast} a_i^{\prime} > 1を満たすパターン\mathbf{p}^{\prime}に対応する制約条件は,双対問題の実行可能領域を通るため,パターン\mathbf{p}^{\prime}を追加して双対問題を解き直すと最適値が小さくなります.双対定理より,線形計画問題とその双対問題の最適値は一致するため,パターン\mathbf{p}^{\prime}を追加することで,線形計画問題の最適値も小さくすなわち改善できることが分かります.
ここで,全てのパターン\mathbf{p}_j \in \{ \mathbf{p}_{k+1},\dots,\mathbf{p}_n \}に対して\sum_{i=1}^m y_i^{\ast} a_{ij}を計算する必要があるように思えます.しかし,以下の整数ナップサック問題を解くことでこの計算を代替できます.
\begin{array}{lll}
\textnormal{最大化} & \displaystyle\sum_{i=1}^m y_i^{\ast} a_i^{\prime}\\
\textnormal{条件} & \displaystyle\sum_{i=1}^m l_i a_i^{\prime} \le L,\\
& a_i^{\prime} \in \mathbb{Z}_+, & i=1,\dots,m.
\end{array}
整数ナップサック問題の最適解\mathbf{p}^{\ast} = (a_1^{\ast},a_2^{\ast},\dots,a_m^{\ast})が\sum_{i=1}^m y_i^{\ast} a_i^{\ast} \le 1を満たせば,\mathbf{p}_{k+1},\dots,\mathbf{p}_nのいずれのパターンを加えても線形計画問題の最適値を改善できないことが分かります.そうでなければ,パターン\mathbf{p}^{\ast}を追加すれば線形計画問題の最適値を改善できます.
この整数ナップサック問題は,母材の長さLと各板材の長さl_iが整数であれば,0-1ナップサック問題と同様に動的計画法で解けます.母材の長さLをv(\le L)で置き換えた整数ナップサック問題の最適値をf(v)とします.このとき,\bar{l} = \min_{i=1,\dots,m} l_iとすると,0 \le v < \bar{l}に対してf(v)=0となります.整数ナップサック問題の最適値f(L)は,v=\bar{l},\dots,Lの順に漸化式
f(v) = \max_{1 \le i \le m, \, l_i \le v} \{ f(v -l_i) + y_i^{\ast} \}
を計算すれば求めることができます.列生成法によって新たに追加されるパターンの数は,改訂単体法の反復回数と同じなので,多くの場合では板材の種類数mの数倍程度で抑えられます.このように,資材切出し問題に対する列生成法では,整数ナップサック問題を解いて得られる新たなパターンを追加して線形計画問題を解く手続きを反復します.整数最適解を求める厳密解法については,分枝限定法と列生成法を組み合わせた分枝価格法(branch-and-price method)が提案されています.
おわりに
お気づきかと思いますが,資材切出し問題はビンパッキング問題(bin packing)を一般化した問題なので,整数ナップサック問題を0-1ナップサック問題に置き換えるだけでビンパッキング問題を解くことができます.このように,あらかじめ可能なパターンを列挙した上でパターンの組合せを求める整数計画問題に定式化する方法はしばしば使われ,配送計画(vehicle routing)や乗務員スケジューリング(crew scheduling)などが代表的な応用事例として知られています.
列生成法の解説は宮本先生による「はじめての列生成法」もありますので,本稿を読んでスッキリしなかった方は,そちらもご一読ください.
追伸
この記事を読んでいただいた皆さんはすでに購入済かと思いますが,講談社より出版されました「しっかり学ぶ数理最適化」をよろしくお願いします.周りの興味を持ちそうな方に薦めていただけると大変に嬉しいです.
Discussion