Zenn
🎄

整数計画ソルバーでシフトスケジューリング問題を解いてみた

2023/12/25に公開
数理最適化
tech

はじめに

無償の整数計画ソルバーでどれぐらいの規模のシフトスケジューリング問題が解けるか確かめたくなったので試してみました。
今回は、久保先生の『Pythonによる実務で役立つ最適化問題100+(3)―配送計画・パッキング・スケジューリング―』のシフトスケジューリング問題を取り上げます。出典は下記の論文で、テストデータはOR-Libraryからダウンロードできます。

M.Krishnamoorthy, A.T.Ernst, D.Baatar, Algorithms for large scale shift minimisation personnel task shcduling problems, European Journal of Operational Research, 219 (2012), 34-48.

論文を読み始めたら期待している問題設定と違ったし、久保先生がサンプルコードを公開してるので、他の論文も探したのですが、問題設定がシンプルでかつテストデータも公開されているものが見つからなかったので、このまま進めることにしました。

問題設定と定式化

複数のジョブにスタッフを割り当てます。各ジョブは開始時刻と終了時刻が決まっており、スタッフを１人割り当てます。スタッフは同時に１つのジョブしか担当できず、いったん処理を始めると中断できません。また、各スタッフはそれぞれ担当可能なジョブが決まっています。このとき、全てのジョブを処理する最小人数のスタッフの割り当てを求める問題を考えます。

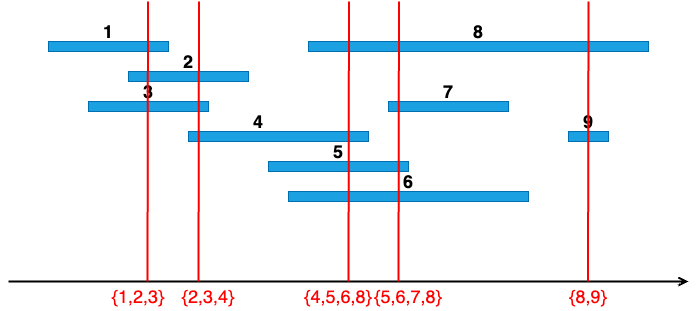
スタッフは同時に１つのジョブしか担当できないので、時刻毎に各スタッフに１つのジョブしか割り当てないよう制約を記述する必要があるように思えます。しかし、実際には、下の例のように一部のジョブの組み合わせのみ制約を記述すれば十分であることが知られています。
これは、処理時間が被るジョブの組み合わせを表した区間グラフの極大クリークを求めることで得られます[1]。
ジョブの集合
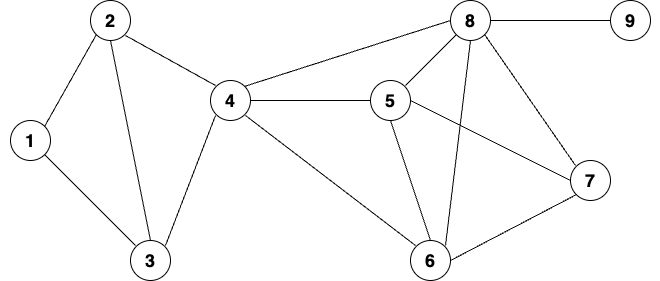
区間グラフ

シフトスケジューリング問題の定式化は以下の通りです。

J = \{ 1,\dots,n \}：ジョブjの集合
W = \{ 1,\dots,m\}：スタッフwの集合
[s_j,f_j]：ジョブjの開始時刻および終了時刻
J_w (\subseteq J)：スタッフwが担当可能なジョブjの集合
W_j (\subseteq W)：ジョブjを担当可能なスタッフwの集合
C = {K_1,\dots,K_p}：区間グラフにおける極大クリークの集合

x_{j,w} \in \{ 0,1 \}：ジョブjにスタッフwを割り当てる
y_{w} \in \{ 0,1 \}：スタッフwを雇用する

\begin{array}{lll} \textnormal{min.} & \displaystyle\sum_{w \in W} y_w\\ \textnormal{s.t.} & \displaystyle\sum_{w \in W_j} x_{j,w} = 1, & j \in J,\\ & \displaystyle\sum_{j \in K_t \cap J_w} x_{j,w} \le y_w, & w \in W, K_t \in C,\\ & y_w \in \{ 0,1 \}, & w \in W,\\ & x_{j,w} \in \{ 0,1 \}, & j \in J, w \in W. \end{array}

１番目の制約は、ジョブjにちょうど１人のスタッフを割り当てることを表します。２番目の制約はスタッフwに同時に１つ以下のジョブしか割り当てられないことを表します。スタッフwにジョブが１つ以上割り当てられるとy_w=1となります。

整数計画ソルバーを用いた実装

今回は、Python-MIPを用いてシフトスケジューリング問題を解くプログラムを作成します。
ソースコードの主要部分のみ紹介します。

下記のクラスを用意して入出力データを格納します。

class Roster:
    def __init__(self):
        self.job = []  # ジョブjの開始時刻と終了時刻[]のリスト
        self.qual = []  # list of J[w]
        self.clique = []  # set of K[t] 

class Solution:
    def __init__(self):
        self.job = {}  # assigned staff for job j
        self.staff = {}  # assigned jobs to staff w

久保先生にならって区間グラフの作成と極大クリークの列挙にはnetworkxを使いました[2]。

def conflict_job(roster):
    # 区間グラフの作成
    graph = networkx.Graph()
    for j in range(len(roster.job)):
        for k in range(j+1, len(roster.job)):
            [start_j, finish_j] = (roster.job)[j]
            [start_k, finish_k] = (roster.job)[k]
            if (start_j <= start_k and start_k < finish_j) or (start_k <= start_j and start_j < finish_k):
                graph.add_edge(j, k)
    # 極大クリークの列挙
    for clq in networkx.find_cliques(graph):
        (roster.clique).append(set(clq))

整数計画ソルバーによるモデルの生成と求解です。ちょっと長いですが、そのまま掲載します。

def solve_roster(roster, sol):
    # 変数の設定
    def set_var(roster, mip_model):
        x = {}
        idx_set = ((w, j) for w in range(len(roster.qual)) for j in (roster.qual)[w])
        for w, j in idx_set:
            x[(j,w)] = mip_model.add_var(var_type='B', name=f'x({j},{w})')
        y = {}
        for w in range(len(roster.qual)):
            y[w] = mip_model.add_var(var_type='B', name=f'y({w})')
        return x, y
    # 制約条件の設定
    def set_cst(roster, mip_model, x, y):
        # 制約1
        for j in range(len(roster.job)):
            qual_set = (w for w in range(len(roster.qual)) if (j,w) in x)  # only qualified staffs
            mip_model.add_constr(xsum(x[(j,w)] for w in qual_set) == 1, name=f'JOB({j})')
        # 制約2
        for w in range(len(roster.qual)):
            for k in range(len(roster.clique)):
                qual_set = (j for j in (roster.clique)[k] if (j,w) in x)
                mip_model.add_constr(xsum(x[(j,w)] for j in qual_set) - y[w] <= 0, name=f'STAFF({w},{k})')
    # 目的関数の設定
    def set_obj(roster, mip_model, x, y):
        num_staff = xsum(y[w] for w in y)
        mip_model.objective = minimize(num_staff)
    # 解の取得
    def get_sol(sol, x, y):
        # get solution
        for (j,w) in x:
            if x[(j,w)].x > 0.5:
                if j in sol.job:
                    print(f'job {j} is already performed!')
                    sys.exit(1)
                else:
                    (sol.job)[j] = w
                    if w not in sol.staff:
                        (sol.staff)[w] = {j}
                    else:
                        (sol.staff)[w].add(j)
    # メイン
    mip_model = Model(solver_name=CBC)  # ソルバーをCBCに設定
    var = set_var(roster, mip_model)
    set_cst(roster, mip_model, *var)
    set_obj(roster, mip_model, *var)
    mip_model.optimize()
    if mip_model.num_solutions:
        get_sol(sol, *var)
    else:
        print('No solution found!')
        sys.exit(1)
    mip_model.clear()

最後に、実行結果の可視化です。今回はこれが一番苦労しました（苦笑）
今回はPlotlyのexpress.timelineを用いました。

def Gantt_chart(roster, sol):
    table = pandas.DataFrame(
                [dict(Job=f'Job{job}', Start=(roster.job)[job][0], Finish=(roster.job)[job][1], Staff=f'Staff{staff}')
                    for staff, job_set in sol.staff.items()
                    for job in job_set])
    table['delta'] = table['Finish'] - table['Start']
    fig = plotly.express.timeline(table, x_start='Start', x_end='Finish', y='Staff', text='Job')
    fig.update_yaxes(autorange='reversed')
    fig.update_layout(yaxis={'dtick':1})
    fig.layout.xaxis.type = 'linear'
    fig.data[0].x = table.delta.tolist()
    fig.show()

ガントチャートを描くだけならfigure_factory.create_ganttがあるのですが、横軸を日付から数値に変更にするのと、同じ色に揃えるのが同時にできませんでした。せっかくコードを書いたので、ここに供養します（ランダムに色を割り当てています）。

def Gantt_chart(roster, sol):
    table = []
    for staff, job_set in sol.staff.items():
        for job in job_set:
            table.append(dict(Task=f'Staff{staff}', Start=(roster.job)[job][0], Finish=(roster.job)[job][1], Job=f'Job{job}'))
    color_list = {}
    for j in range(len(roster.job)):
        color_list[f'Job{j}'] = tuple(random.random() for _ in range(3))
    fig = figure_facactory.create_gantt(table, group_tasks=True, index_col='Job', colors=color_list)
    fig.update_layout(xaxis_type='linear')
    fig.show()

計算実験

まずは、問題例data_1_23_40_66.dat(スタッフ23人、ジョブ40個)で実行すると、以下の結果が得られました。1秒足らずで最適解（必要人数20人）が得られました。
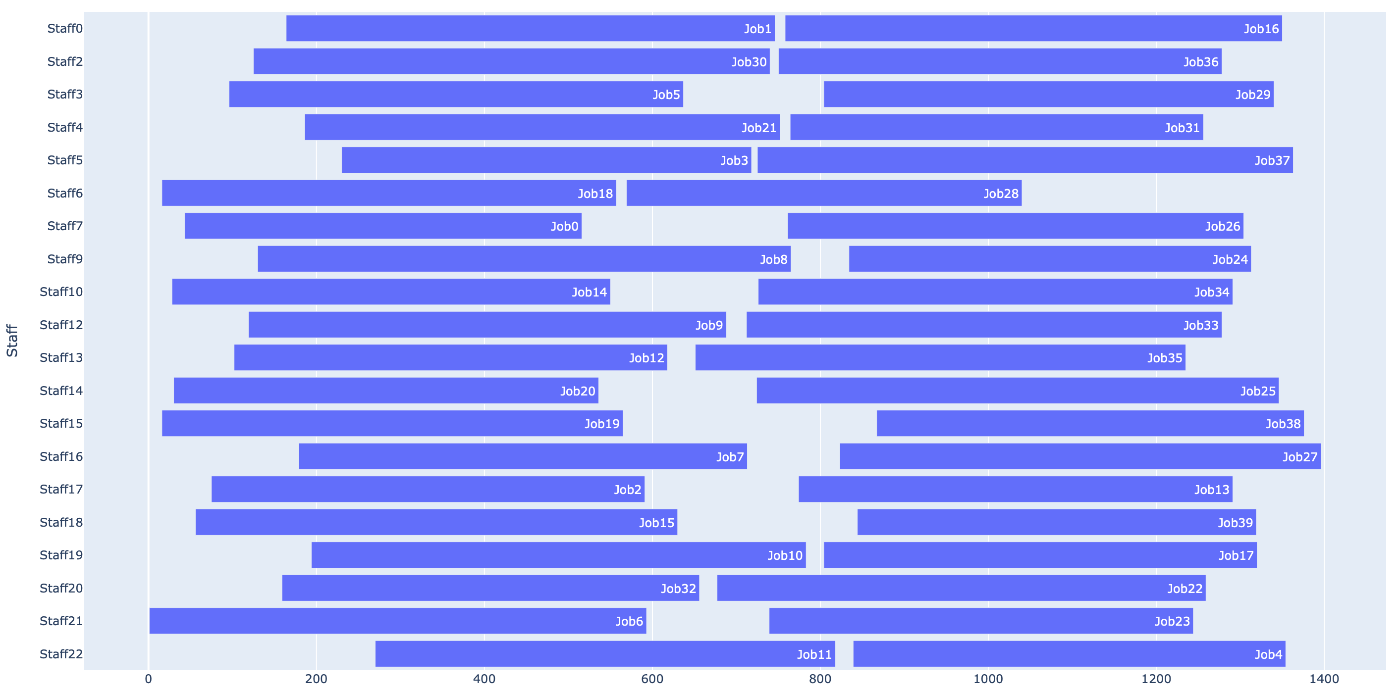
実行結果の例

今回は、MacBook Air(15-inch, M2)で計算実験しました。
論文でCPLEX11.2を用いて最適解が得られた問題例に対して、整数計画ソルバーの実行時間を最大60秒に設定してプログラムを実行しました。テストデータに対する結果は以下の通りです。
2012年の論文なので、10年前のSOTAと比べて遜色ないという感じでしょうか。

問題例 スタッフ数 ジョブ数 必要人数 計算時間(秒)
#1 23 40 20 0.14
#2 24 40 20 0.08
#3 25 40 20 0.16
#4 23 59 20 0.13
#5 25 60 20 0.13
#6 48 80 40 0.75
#7 51 80 40 0.73
#8 48 85 40 0.93
#9 49 104 40 0.59
#10 51 111 40 1.85
#11 24 119 20 0.36
#12 49 119 40 1.38
#13 25 120 20 0.79
#14 75 124 60 1.64
#15 72 126 60 1.51
#16 75 131 60 3.48
#17 23 139 20 1.68
#18 48 160 40 3.04
#19 97 160 80 2.20
#20 99 163 80 2.64
#21 93 175 80 3.62
#22 47 180 40 4.89
#23 74 180 60 2.84
#24 110 200 100 3.77
#25 120 200 100 3.33
#26 116 203 100 7.58
#27 49 204 40 5.84
#28 75 208 60 7.51
#29 22 219 20 2.92
#30 25 219 20 2.73
#31 90 230 80 10.25
#32 70 236 60 6.65
#33 76 240 60 7.95
#34 152 240 120 4.77
#35 171 280 140 7.96
#36 175 280 140 10.48
#37 145 321 120 17.36
#38 147 347 120 65.48
#39 45 351 40 14.93
#40 138 360 120 10.82
#41 144 360 120 44.99
#42 101 380 80 42.56
#43 156 387 140 61.91
#44 121 400 100 14.45
#45 67 420 60 19.06
#46 147 423 120 46.08
#47 150 430 120 35.96
#48 120 434 100 timeout
#49 211 446 180 timeout
#50 187 447 160 46.57
#51 196 480 160 27.68
#52 205 480 160 66.19
#59 70 525 61 timeout
#66 348 600 302 timeout
#67 371 600 300 70.40

おわりに

本記事では、無償の整数計画ソルバーでシフトスケジューリング問題を解いてみました。テストデータに対する計算実験では、規模の大きな問題例でも1分程度で最適解を得ることができました。ちなみに、論文ではさらに大規模な問題例を解くためのヒューリスティックも提案されていますので、興味を持たれた方は読んでみて下さい。
さて、今回の整数計画モデルが実務に現れるシフトスケジューリング問題に広く活用できるかと言うと正直に言って微妙です。シフトスケジューリング問題には非常に多くのバリエーションがあります。残念ながら、今回取り上げた論文の問題設定は小売や飲食の店舗スタッフのシフト作成にはあまり適合しない気がします。引き続き他の論文も調べて、どこかの機会にまとめてご報告できればと思います。

脚注

  1. 詳細は論文を参照して下さい。 ↩︎

  2. 論文では区間グラフの極大クリークを列挙する効率的なアルゴリズムが紹介されています。 ↩︎

Discussion