スコアベース生成モデルと Consistency Models

本記事は、裏アドベントカレンダー「ほぼ横浜の民2024」の9日目の記事です。最近は業務でも生成モデルを扱うことが多く、生成モデルの高速化にも興味が出てきたので書いてみようと思います。生成モデルと言いつつ、本記事では拡散モデルに絞って基本的な理論とその高速化手法の１つである Consistency Models についてざっくり説明していこうと思います。あまり数学的に厳密に説明できていない部分もあり、私なりの解釈に基づく説明も入ってしまっていますがご容赦ください。

この記事を読んでわかること

• 拡散モデルがデータを生成する仕組み
• スコアベース生成モデルとは？ SDE, PF ODE とは？
• Consistency Models とは？

拡散モデルの理論を振り返ってみる

拡散モデルのコンセプト

改めて拡散モデルの理論をざっくりと説明したいと思います。拡散モデルは生成モデルの一種であり、以下の２つのプロセスから構成されます。なお、以下の図では実データの分布における時刻を $t=0$、十分にノイズが付与された時刻を $t=T$、各時刻におけるサンプルを $x_t$ としています。

• 順拡散過程：微小なノイズを繰り返しデータに付与し、完全なノイズ状態とする
• 逆拡散過程：各時刻で付与された微小なノイズ量を繰り返し推定し、最終的なデータを生成する

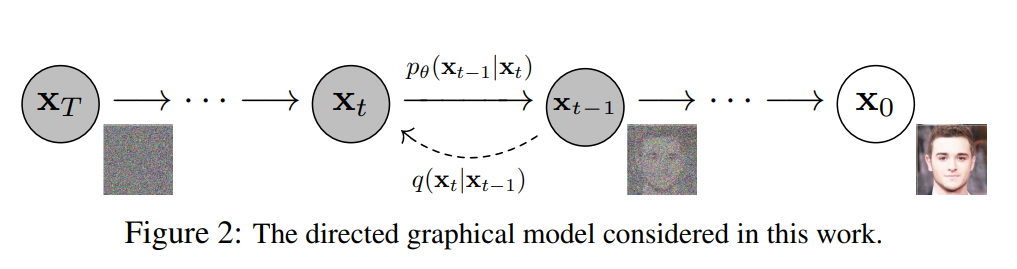
有名な拡散モデル手法である上図の DDPM (Denoising Diffusion Probabilistic Models) は離散的な拡散過程を考えるものですが、連続的な拡散過程を考える研究の流れもあり、そちらでは拡散モデルは「スコアベース生成モデル」として定義されることが多いです。今回、Consistency Models を理解するにあたって、拡散モデルをスコアベース生成モデルとして解釈するところから始めようと思います。（論文の流れがそんな感じです）

補足：生成モデルと拡散モデル
生成モデルでやりたいこととしては、実データの分布 $p_0(x)$ から所望のデータ $x_0$ をサンプリングすることですが、一般的に $p_0(x)$ は非常に難しい分布をしているため、いきなり $p_0(x)$ を獲得する、すなわち $p_0(x)$ からのサンプリングを直接実現することは難しいです。そこで多くの生成モデルでは既知の簡単な分布 $p_T(x)$ から実データの分布 $p_0(x)$ への変換を学習して $p_0(x)$ を獲得するというアプローチをとることが多く、その分布変換のアプローチの１つが拡散モデルになります。拡散モデルでは既知の簡単な分布として $p_T(x)$ がガウス分布などで定義されており、このノイズの分布と実データ分布 $p_0(x)$ の変換を拡散過程を通して獲得しています。

連続的な拡散過程（stochastic differential equation: SDE）

連続的な拡散過程を考えるとき、拡散モデルの順拡散過程は以下の確率微分方程式 (stochastic differential equation: SDE) で定義されます。

$$d\bold{x_t} = \bold{f}(\bold{x_t}, t)dt + g(t)d\bold{w_t}$$

数式において、$\bold{f}(\cdot)$ はドリフト係数、$g(\cdot)$ は拡散係数、$d\bold{w_t}$ は微小なホワイトノイズとなっています。イメージとしては、微小な時間 $dt$ が経過したときの分布の傾き(ドリフト量)が $\bold{f}(\bold{x_t}, t)$ で決まり、その周辺におけるばらつきがランダム性をもって $g(t)d\bold{w_t}$ の項によって決定されていると捉えることができるのではないでしょうか。

以下の図は、連続的な拡散過程における SDE の軌道を可視化したものになります。実データ $\bold{x}(0)$ は複雑な分布 $p_0(\bold{x})$ を持っていて、そこに対して確率微分方程式で定義された拡散過程を適用しています。十分にノイズが付与されたときのサンプル $\bold{x}(T)$ は簡単なノイズ空間の分布 $p_T(\bold{x})$ を持っており、多くの拡散モデルではこの $p_T(\bold{x})$ がガウス分布で定義されています。図の例ですと、実データの分布は２つのピークを持っていて、それぞれのピーク付近から3サンプルずつ計6サンプルのデータを取り出してそれらにノイズを付与していっているようです。（もちろん実データの分布はかなり複雑ですが説明のためにこのような分布で図示されています）

ノイズが付与された各時刻の画像も一緒に可視化すると以下のような感じです。この動画は、実データの分布 $p_0(\bold{x})$ から４枚の画像を取り出してそこにノイズを付与していった場合の SDE 軌道のイメージ図になっています。こうやって可視化してみると、ランダム性をもった過程なので微分方程式の軌道もかなり不安定になっていることがわかります。

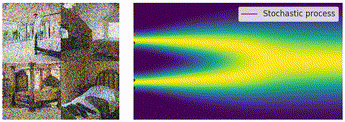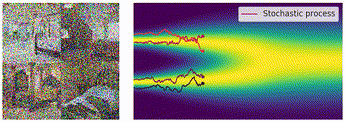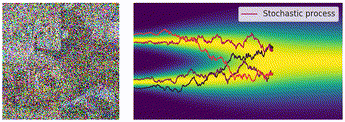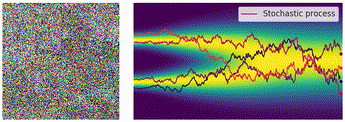
連続的な逆拡散過程（Reverse SDE）

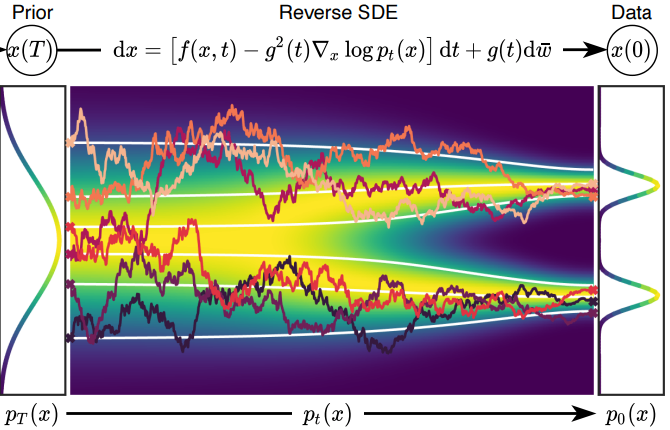
なお、任意のSDEには逆SDEを定義することができ、この逆SDEをSDEのソルバーなどで数値的に解くことで、逆拡散過程を解くことができます。逆SDEは以下で定式化できます。

$$d\bold{x_t} = \lbrack \bold{f}(\bold{x_t}, t) + g^2(t){\nabla}_{\bold{x}} \log p_t(\bold{x_t}) \rbrack dt + g(t)d\bold{w_t}.$$

逆SDEを解くときには任意の時刻 $t$ におけるデータの分布 $p_t(\bold{x})$ のスコア関数と呼ばれる ${\nabla}_{\bold{x}} \log p_t(\bold{x})$ を求める必要があります。実際の拡散モデルの学習では、この時間依存のスコア関数を $\bold{s}_{\phi}(\bold{x}, t) \approx {\nabla}_{\bold{x}} \log p_t(\bold{x})$ となるように学習によって獲得します。これが拡散モデルがスコアベースの生成モデルと言われる所以になります。

今回も先ほどのように図でイメージを確認しておきます。今回は逆拡散過程にあたるので、ノイズサンプル $\bold{x}(T)$ の簡単な分布 $p_T(\bold{x})$ に対して、逆SDEを数値的に解くことでノイズを徐々に除去していき、最終的に実データの分布 $p_0(\bold{x})$ に近い生成データ $\bold{x}(0)$ を得ることができます。

ノイズ画像から徐々にノイズが除去されていく過程も一緒に可視化したものがこちらになります。こちらも順拡散過程と同様に、SDEの軌道がかなり不安定になっていることがわかります。

補足：スコア関数とは？
統計学や機械学習の文脈で利用されることが多く、「対数尤度の勾配」として定義されています。生成モデルの文脈におけるスコア関数 ${\nabla}_{\bold{x}} \log p_t(\bold{x})$ は、データ $\bold{x}$ を微小に動かしたときの対数尤度の変化量と解釈できるので、逆拡散過程におけるノイズ除去の方向を決める重要な関数になっています。

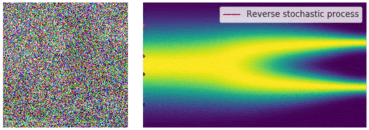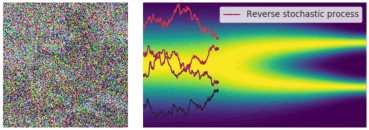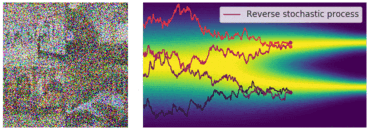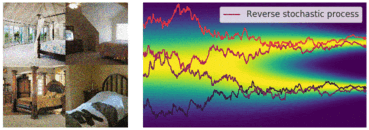
連続的かつ決定論的な過程で制御しやすくする（Probability Flow ODE）

SDEによっても高品質な生成は可能なのですが、定式化にランダムなノイズ頂が含まれるために厳密に正確なスコア関数を求めることができていません。この問題に対して提案されたのがProbability Flow ODEです。PF ODEは以下の式で定義されます。

$$d\bold{x_t} = \bigl[ \bold{f}(\bold{x_t}, t)dt + \frac{1}{2} g(t)^2 {\nabla}_{\bold{x}} \log p_t(\bold{x_t}) \bigr] dt.$$

実は、任意のSDEの周辺分布 $p_t(\bold{x})$ を変更することなく常微分方程式に変更することが可能で、このSDEに対応する常微分方程式が PF ODE になります。PF ODEは、SDEからランダム性を排除して決定論的な過程にすることで可逆性を担保しています。これにより理論的に正確なスコア関数の計算が可能になります。SDEの説明に用いた図をもう一度見てみると、実は PF ODE の軌道も記載されており、SDEの軌道と比較してかなり滑らかな軌道になっていることがわかります。PF ODEのメリットは、SDEと同じ周辺分布を維持しつつ、決定的サンプリングが可能であるが故に再現性が高く、不安定性やばらつきが低減されるために高品質かつ安定したサンプリングが可能であることだと解釈できます。

補足：確率微分方程式と常微分方程式
常微分方程式（ODE）は、未知関数の微分が決定論的な関数として定まるので、初期条件が与えられるとその解は一意に求まる場合が多いです。一方、確率微分方程式（SDE）は、ODEの形に加えてランダムな項、たとえばブラウン運動のようなノイズ項が含まれているため、解は確率過程となります。

ODE: $dx = f(x, t)dt$
SDE: $dx = f(x, t)dt + g(x, t)dB_t$

PF ODE を扱いやすい過程とする (empirical PF ODE)

ここで、PF ODEの式を解析的に扱いやすい過程とするために、ドリフト項 $\bold{f}(\bold{x}, t) = 0$、拡散係数項 $g(t) = \sqrt{2t}$ の仮定をおきます。これによって、PF ODEの解が初期値に対して平均 0 分散 $t$ のガウス分布 $\textit{N}(0, t^2\bold{I})$ を足しこんでいくというシンプルな過程になるようにしています。この仮定をさきほどの PF PDE の定義に代入してあげると以下の式が得られます。

$$\frac{d\bold{x}}{dt} = - t \bold{s}_{\phi}(\bold{x}, t)$$

この式を経験的 PF ODE (Empirical PF ODE) と呼びます。ここで、時刻 $t=T$ におけるノイズに近いサンプルの予測値 $\hat{x_T}$ はシンプルなガウス分布 $\textit{N}(0, t^2\bold{I})$ に従うものとして初期値を設定できます。そして任意の数値 ODE ソルバーで $t=T$ から $t=0$ へ向けて解 $\hat{x_t}$ を求めることで PF ODE の解軌道をもとめることができ、最終的に実データの分布 $p_0(\bold{x})$ からのサンプルの近似として、生成データ $\hat{x_0}$ を得ることができます。なお、実際の計算においては、数値的な不安定性を回避するために微小な $\epsilon$ を設定し、$t=\epsilon$ において ODE ソルバーを停止して、$\hat{x_{\epsilon}}$ を最終的な生成サンプルとみなすことが一般的なようです。

拡散モデルとスコアベース生成モデル
実は拡散モデルとスコアベース生成モデルは互いに密接にかかわって発展してきたわけではなく、独立して研究・提案されたものになります。ノイズを用いてデータをノイズに変換し、そこから元のデータへと逆向きにサンプリングする過程は共通していたものの、学習やサンプリングのアプローチが異なるために当初は両者の関係性は表面的なものであるという見方が多かったようです。ただ、近年では本質的に同じ学習を行っていることがわかってきており、同じモデルファミリーを異なる視点から解釈したものであるといえそうです。具体的には、スコアベースモデルと拡散確率モデル（DDPM など）を 連続時間の確率微分方程式（SDE） を介して捉えると、どちらも「ノイズのスケールを無限に細かく離散化した場合には同じ理論的枠組みに収まる」ということが示されています。

拡散モデルは推論コストが高い

ここまで連続的な拡散過程の定式化を見てきたことで、拡散過程は微分方程式で表現することが可能で、定式化を工夫することにより安定的な解軌道を獲得することができるとともに既存のODEソルバーで計算できることがわかってきました。ただ、高速なODEソルバーの利用や蒸留などの高速な推論を行うさまざまな工夫がなされていたとしても、最低でも10回程度のforwardが必要なことには変わりなく、拡散モデルの推論が高コストであるということは明確な問題として残っていました。

この問題に対する解決策として「1ステップで推論する」というアイデアが提案され、これが Consistency Models のコンセプトとなっています。前置きが長くなりましたが、ここからは Consistency Models の内容を具体的に説明していきます。

Consistency Models とは？

基本的なアイデア

どのように１ステップで推論するのかと言うと、「ODE軌道上のどの位置からも一貫して同一の終点を予測できるようにする」という学習を行います。この一貫した予測に関わる制約から Consistency Models（一貫性モデル）と呼ばれています。PF ODE の解軌道 $\{\bold{x_t}\}^{T}_{t=\epsilon}$ が与えられたときに、一貫して終点 $\bold{x_0}$ (実際には $\bold{x_{\epsilon}}$) を予測する Consistency Function $\bold{\textit{f}}(\bold{x}, t)$ を学習することになり、この $\bold{\textit{f}}(\bold{x}, t)$ に対しては以下のような式が成立します。

$$\bold{\textit{f}}(\bold{x_T}, T) = ... = \bold{\textit{f}}(\bold{x_{t'}}, t') = \bold{\textit{f}}(\bold{x_t}, t) = ... = \bold{\textit{f}}(\bold{x_0}, 0) = \bold{x_0}$$

$\bold{\textit{f}}(\bold{x}, t)$ の学習方法としては、以下の２つが存在します。

1. Consistency Distillation (CD): 既存の拡散モデルを蒸留して学習する
2. Consistency Training (CT): ゼロから一貫性モデルを学習する

Consistency Distillation (CD): 既存の拡散モデルを蒸留して学習する

具体的には、以下の式で「同一ODE軌道において隣接したサンプル点が同じ終点を予測する」という条件で学習を行います。

$$\mathcal{L}_{CD}^{N}(\boldsymbol{\theta}, \boldsymbol{\theta}^{-}) = \mathbb{E}_{\mathbf{x}, \epsilon, n} \left[ \lambda(t_n) d \left( f_{\boldsymbol{\theta}} (\mathbf{x}_{t_{n+1}}, t_{n+1}), f_{\boldsymbol{\theta}^{-}} (\hat{\mathbf{x}}_{t_n}^{\phi}, t_n) \right) \right]$$

少し複雑に見えますが順を追ってみていきます。

1. 任意の時刻の一貫性モデルの予測値を計算する：任意の時刻 $t_{n+1}$ およびそのときのサンプル $\mathbf{x}_{t_{n+1}}$ に対して一貫性モデルの終点の予測 $f_{\boldsymbol{\theta}} (\mathbf{x}_{t_{n+1}}, t_{n+1})$ を計算します。

2. 同一 ODE 軌道上において隣接する時刻の予測値を計算する：同一 ODE 軌道上における隣接する時刻のサンプルはどのように計算されるかというと、学習済みの拡散モデル $\phi$ によって $\hat{\mathbf{x}}_{t_n}^{\phi}$ として予測されます。このとき、同じ一貫性モデルを使って $f_{\boldsymbol{\theta}} (\hat{\mathbf{x}}_{t_n}^{\phi}, t_n)$ を計算して損失を計算したくなるところではありますが、学習の安定化のために指数移動平均モデル（EMA）を使って隣接点の予測値 $f_{\boldsymbol{\theta}^{-}} (\hat{\mathbf{x}}_{t_n}^{\phi}, t_n)$ を得ます。

3. 一貫性モデルの予測値が隣接点同士で同じになることを計算する：隣接点における終端の予測を距離関数 $d$ によって評価します。評価関数としては、$l_1$ 距離、$l_2$ 距離、Learned Perceptual Image Patch Similarity (LPIPS) などさまざまな距離関数が利用可能です。なお、論文の結果では LPIPS が最も性能的に良かったみたいです。また、$\lambda(t_n)$ という重みづけも含まれていますが、常に1としておいて問題はなかったようです。最終的にこの距離を最小化するような学習を行います。

補足：Consistency Loss のお気持ちを理解する
一瞬、各時刻において $\bold{\textit{f}}(\bold{x_{t'}}, t') = \bold{x_0}$、$\bold{\textit{f}}(\bold{x_{t}}, t) = \bold{x_0}$... のように学習していけば良いような気もしますが、この損失設計がうまくいくのであればそもそも拡散モデルにおける多段の推論処理が不要という話になります。これがなぜうまくいかないのかを考えてみるとノイズがかなり付与された状態だと、その正解がどの画像にもなりうるので $\bold{\textit{f}}(\bold{x_{t}}, t) = \bold{x_0}$ という個別のシンプルな損失ではうまくいかないというのは想像できそうです。

Consistency Training (CT): ゼロから一貫性モデルを学習する

次に既存の拡散モデルを用いずに一貫性モデルを学習する方法を紹介します。損失関数は以下で定式化されます。

$$\mathcal{L}_{CT}^{N}(\theta, \theta^-) = \mathbb{E}_{\mathbf{x}, \epsilon, n} \left[ \lambda(t_n) d \Big( f_{\theta}(\mathbf{x} + t_{n+1} \epsilon, t_{n+1}), f_{\theta^-}(\mathbf{x} + t_n \epsilon, t_n) \Big) \right]$$

Consistency Distillation と非常に似た定式化になっていることがわかります。この定式化の理論的な詳細は省きますが、「同じノイズを異なる強度でデータに付与する」という処理によって同一ODE軌道上の隣接データのサンプリングを実現しています。なお、学習済み拡散モデルがスコアを正しく推定できている場合には、Consistency Distillation も Consistency Training も理論的には同じということがわかっています。

Consistency Models の推論

Consistency Models の推論は基本的に1回の forward だけで実現できますが、forward の回数を増やして生成品質を向上させることも可能です。具体的には、一度生成された $\bold{x_0}$ にノイズを付与して任意の時刻までさかのぼったサンプル $\bold{x_t}$ を取得してからもう一度 forward を行います。下の結果では、上段が既存の拡散モデル（forward 79回）、中段が Consistency Training（forward 1回）、下段が Consistency Models（forward 2回）になっています。この結果から、Consistency Models の少ない評価回数でも既存の拡散モデルと類似した画像を生成できることや、2回に評価回数を増やして生成品質を向上できていることが確認できます。また、この結果は同一の初期ノイズから生成されているため、同一ODE軌道上の問題として Consistency Models の学習が機能していることもわかります。

まとめ

今回は離散時間における拡散過程を扱ったDDPMの説明に始まり、連続時間における拡散過程とも捉えることができるスコアベース生成モデルについてざっくりと概念を説明し、最終的には Consistency Models について紹介しました。Consistency Models の後継の研究として Latent Consistency Models、Improved Consistency Models、Consistency Trajectory Models などいくつかあるのですが、今回はここまでにしておきます。最後まで読んでいただきありがとうございました。

Reference

• Jonathan Ho et al. “Denoising diffusion probabilistic models.” arxiv Preprint arxiv:2006.11239 (2020).
• Yang Song, et al. “Score-Based Generative Modeling through Stochastic Differential Equations.” ICLR 2021.
• Song et al. “Consistency Models” arxiv Preprint arxiv:2303.01469 (2023)
• What are Diffusion Models?
• Generative Modeling by Estimating Gradients of the Data Distribution
• 【AI論文解説】Consistency ModelsとRectified Flow ~解説編Part1~