素因数分解とRSA暗号の関係
唐突に「極黒のブリュンヒルデ」が読みたくなり、
漫画を買って読んでいた。
早速読み始めると、
カズミが登場する場面で次のような話が出てきた。

「まさかお前、素因数分解が出来るのか?」
「ネットには当然セキュリティがある、その暗号の鍵に使われているのは巨大な素数なんだ」
「素因数分解をするには膨大な時間がかかるという前提があって成り立つセキュリティだ」
大学でここらへんを学んだ記憶は無いし、
気になったので調べてみる。
(調べてたら、サマーウォーズもRSA暗号を使った話だったらしい)
RSA暗号
まず、Wikipediaを見てみる。
RSA暗号(RSAあんごう)とは、桁数が大きい合成数の素因数分解問題が困難であることを安全性の根拠とした公開鍵暗号の一つである。 暗号とデジタル署名を実現できる方式として最初に公開されたものである。
確かに、素因数分解の仕組みを利用したものらしい。
RSA暗号方式は、1977年に発明され、発明者であるロナルド・リベスト、アディ・シャミア、レオナルド・エーデルマンの原語表記の頭文字をつなげてこのように呼ばれる。
ちなみに、RSAは発明者の頭文字らしい。
全体の流れを図にすると次のようになると思う。
公開鍵暗号方式なので、秘密鍵と公開鍵の2つの鍵を生成して、公開鍵だけ相手に共有する形になってる。
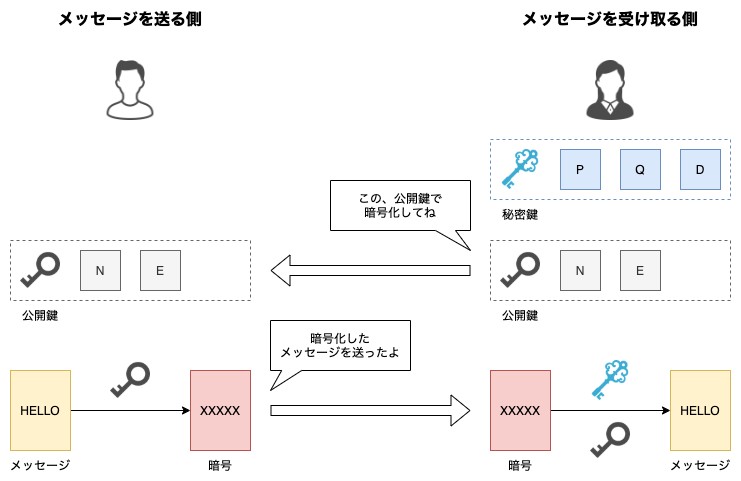
続いて細かい部分を確認してみる。
数学の難しい話はナシにして、できるだけ分かりやすくまとめたいと思う。
鍵生成
鍵は秘密鍵と公開鍵の2つが必要となる。
この鍵として必要となる値を順番に用意していく。
まず、任意の素数のペア P・Q を用意する。
この時、PとQを掛け算した値を N とする。
- P = 7
- Q = 11
- N = P * Q = 77
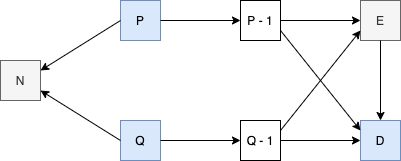
次に、(P - 1) * (Q - 1) と互いに素となる値 E を用意する。
- (P - 1) * (Q - 1) = 60
- E = 13
また、(E * D) / ((P - 1) * (Q - 1)) が 余り 1 となるような値 D を用意する。
- (13 * 37) / ((7 - 1) * (11 - 1)) = 8 余り 1
- D = 37
これで、下準備はOK。
P・Q・Dを秘密鍵とし、N・Eを公開鍵とする。
- 秘密鍵:P・Q・D
- 公開鍵:N・E
なので、N・Eを相手に共有し、P・Q・Dは自分だけの秘密にしておく。
暗号化
秘密鍵と公開鍵が準備できたので、メッセージを暗号化してみる。
暗号化には先ほど生成した、公開鍵を使う。
ここでは、HELLO を暗号化する前のメッセージとしてみる。
- メッセージ:HELLO
まず、公開鍵である数値NとEを使って暗号化するために、メッセージを数値で表現する必要がある。
ここでは、次の表に従ってアルファベットと数値を対応させる。
| アルファベット | 数値 |
|---|---|
| A | 1 |
| B | 2 |
| C | 3 |
| ... | ... |
| X | 24 |
| Y | 25 |
| Z | 26 |
表に従って、メッセージ HELLO を数値に変換すると次のようになる。
- HELLO:8・5・12・12・15
この数値に変換されたメッセージを使い暗号化してみる。
メッセージの各数値XをE乗し、Nで割った余りの値Yに変換する。
- (X ^ E) / N ... 余り Y
- (8 ^ 13) / 77 ... 余り 50
- (5 ^ 13) / 77 ... 余り 26
- (12 ^ 13) / 77 ... 余り 12
- (12 ^ 13) / 77 ... 余り 12
- (15 ^ 13) / 77 ... 余り 64
- HELLO:50・26・12・12・64

これで暗号化されたメッセージを生成できた。
これを、秘密鍵を持っている相手に送って、復号してもらう。
復号
最後に、暗号化されたメッセージを復号して、元のメッセージになるか確認してみる。
複合するには、暗号化されたメッセージの各値YをD乗し、Nで割った余りが元の値Xとなるはず。
また、数値とアルファベットの変換は暗号化したときの対応表と同じでOK。
- (Y ^ D) / N ... 余り X
- (50 ^ 37) / 77 ... 余り 8
- (26 ^ 37) / 77 ... 余り 5
- (12 ^ 37) / 77 ... 余り 12
- (12 ^ 37) / 77 ... 余り 12
- (64 ^ 37) / 77 ... 余り 15
- HELLO:8・5・12・12・15
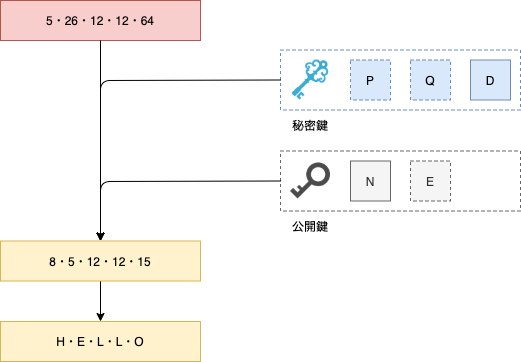
元のメッセージと同じになった。
ここで、DはPとQから生成された値であり、PとQはNを素因数分解する事で得られる。
しかし、「桁数が大きい合成数の素因数分解問題が困難である」ので、Nを公開鍵として共有しても現実的な時間で計算するのは難しいのだろう。
鍵長
RSA暗号では鍵長に応じて、素数P・Qの値の範囲が変わってくる。
つまり、鍵長を大きくすれば桁数が多い素数を扱えるということになる。
これが、「桁数が大きい合成数の素因数分解問題が困難である」という点とふ再びつながってくる。
2048bitや4096bitといった鍵長を指定すれば、桁数が多く計算が困難である強力な暗号化を実現できるということなのだろう。
また、SSH用の鍵を作る際に4096bitを指定するのを推奨している記事を見かける。
確かに、RSA Factoring Challenge - Wikipedia を見た感じだと、1024bitが計算されてしまう日はそう遠くないのかも?
まとめ
情報系の学科であれば当たり前に知っている内容なのかもしれないが、新しい知識を得られてよかった。
それにしても、素因数分解という物凄くシンプルな物を、暗号化方式として応用してしまうのはすごい。
参考文献
※ RSA暗号に関して専門知識を有しているわけではないので、誤った情報の可能性もあります。
※ 間違ってたら、やさしくご指摘お願いします。
Discussion