掛け算から理解する相関係数はなぜ直線的な関係しか表さないのか

相関係数についてよく言われる注意点として、「相関係数は直線的な関係しか表さない」というものがあります。
これについて、円や二次関数の形をしたデータ分布の例を出して、このデータの相関係数は0になるんだよという説明がされたりします。
この説明について「なるほど」とはなるものの、一部の反例をあげただけでごまかされているような気がして、モヤッとしてしまいました。

なぜ相関係数が直線的な関係しか表すことができない原理はどうなっているのか調べてみました。

先に結論

先に結論だけ述べると、

相関係数はデータ分布の重心からの変化の傾向を単一の正規化された値として表現した指標なので直線関係しか表しようがありません。

ということなのですが、よくわかりませんね。相関係数はビジネスの場面などでもよく使われたりしますが、きちんと理解しようと思うと意外と複雑な前提が積み重なっていることがわかりました。

この記事では以下の手順で数値の類似度を表す指標について解説することで、相関係数を中学生レベルの知識に紐付けて理解することを目指します。

• 掛け算は類似度だ
• 内積は複数点対応した掛け算だ
• 共分散は中心化した内積だ
• 相関係数は正規化した共分散だ

掛け算は類似度だ

相関係数が直線的な関係しか表さないことを理解するために、まず最初に理解する必要があることは「掛け算は類似度」だと言うことです。

どういうことでしょうか?
2つの実数x, yがあったとして、積xyの符号を考えてみましょう。

• 積xyが正の場合、xとyはお互いに同傾向であり、類似していると言える
• 積xyが負の場合、xとyはお互いに逆傾向であり、類似していないと言える。
• 積xyが0の場合、xとyはお互いに無関係であり、類似度の評価はできない。

ここで言う類似度は、数直線上での向き(+ or -)のことを指します。
つまり、数直線上での向きが一致していれば似ている数字、逆であれば似ていない数字であると解釈しているということです。

中学生の時に習った、「符号が同じもの同士を掛けると正の数になり、符号が違うもの同士を掛けると負の数になる」という掛け算の法則の見方を変えると掛け算を類似度の指標としてみなすことができるということです。

ここまではそこまで難しいことはないと思います。
念のため例を上げると、
3と8の積は正の数なので似ており、3と-8の積は負の数なので似ていないと言えるということです。

内積は複数点対応した掛け算だ

ここからは高校数学レベルの知識が必要になってきますが、なるべく平易に説明できるようにがんばります。

まず内積とは何だったか復習から始めましょう。まずは内積の定義を確認しましょう。
n次元ベクトルa, bを成分表示で

$$a=(a_1, a_2, ..., a_n)^T, b=(b_1, b_2, ..., b_n)^T$$

とすると、
内積は

$$a \cdot b = a_1b_1 + a_2b_2 + ... + a_nb_n = \sum_{i=1}^n a_ib_i$$

のように定義できます。

要するに、内積とは掛け算の合計だと考えてもらえると良いです。

ここで掛け算は類似度だということを思い出してもらうと、内積は数字のペアごとの類似度の合計をとっている演算だと解釈することができます。

内積の解釈の仕方は以下のようなものになります。

• 内積$a \cdot b$が正なら、2つのベクトルaとbは上がり下がりのタイミングが同傾向で、類似している
• 内積$a \cdot b$が負なら、2つのベクトルaとbは上がり下がりのタイミングが逆傾向で、類似していない
• 内積$a \cdot b$が0なら、2つのベクトルaとbは上がり下がりのタイミングがまったく無関係で、傾向を評価することはできない。

例えば、$a=(0, 1, 0, -1), b=(0, 2, 0, -2), c=(0, -1, 0, 1), d=(1, 0, -1, 0)$だった場合を考えてみましょう。

ベクトルaとbの内積は、

$$a \cdot b = 0 \cdot 0 + 1 \cdot 2 + 0 \cdot 0 + -1 \cdot -2 = 0+2+0+2=4$$

で正なので、aとbの傾向は類似している。
実際aの要素を2倍するとbと等しい。

ベクトルaとcの内積は、

$$a \cdot c = 0 \cdot 0 + 1 \cdot -1 + 0 \cdot 0 + -1 \cdot 1 = 0-1+0-1=-2$$

で負なので、aとcの傾向は逆である。
実際aの要素符号を反転させるとcと等しい。

ベクトルaとdの内積は、

$$a \cdot d = 0 \cdot 1 + 1 \cdot 0 + 0 \cdot -1 + -1 \cdot 0 = 0+0+0+0=0$$

で0なので、aとdの傾向は無関係と言えます。
実際、Aを定数を足したり定数倍してもDにはなりません。

(各要素に別々の数字を足せば同じになるという反論があるかもしれませんが、それはAの性質を全く変えてしまうことになるのでご法度とさせてください。)

ここまでの議論で掛け算が数直線上での方向という意味での類似度を表し、
内積が掛け算を多次元に拡張して数字の集合レベルでの上がり下がりの方向の類似度を表すことが分かりました。

ちなみに

余弦定理を利用することで内積の定義から相関係数(コサイン類似度)を導き出すことができます。
そこから、相関係数はコサインだと理解でき、それはそれで相関係数の直感的な理解に繋がります。
詳しくは以下の解説が分かりやすいです。
「内積が見えると統計学も見える」第5回 プログラマのための数学勉強会 発表資料

共分散は中心化した内積だ

ここから数学の世界を離れて、ようやく統計学の世界に入っていきます。
いままではあえて数字の集合と表現していたものも統計学っぽくあえてデータと表現します。
まずは、共分散の定義を確認しましょう。

$$\displaystyle Cov(x,y) = \frac{1}{n}\{(x_1-\bar{x})(y_1 - \bar{y})+...+(x_n - \bar{x})(y - \bar{y})\} = \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})$$

この形どこかで見たことありませんでしょうか?
そうです、内積の定義とほとんど同じです。

違いは内積が単純な数値の掛け算になっているのに対して、共分散は数値から平均を引いたもの(偏差)の掛け算になっていることだけです。

つまり、共分散も数字の集合の上げ下げの傾向の類似度を表す指標だと言えます。

数値から平均値を引く操作のことを中心化と言いますが、この中心化という操作はどのような意味で、中心化のメリットはどのようなものなのでしょうか?
これについて考察していきましょう。

中心化とは、下記のようにデータの重心を原点に移動させる操作です。

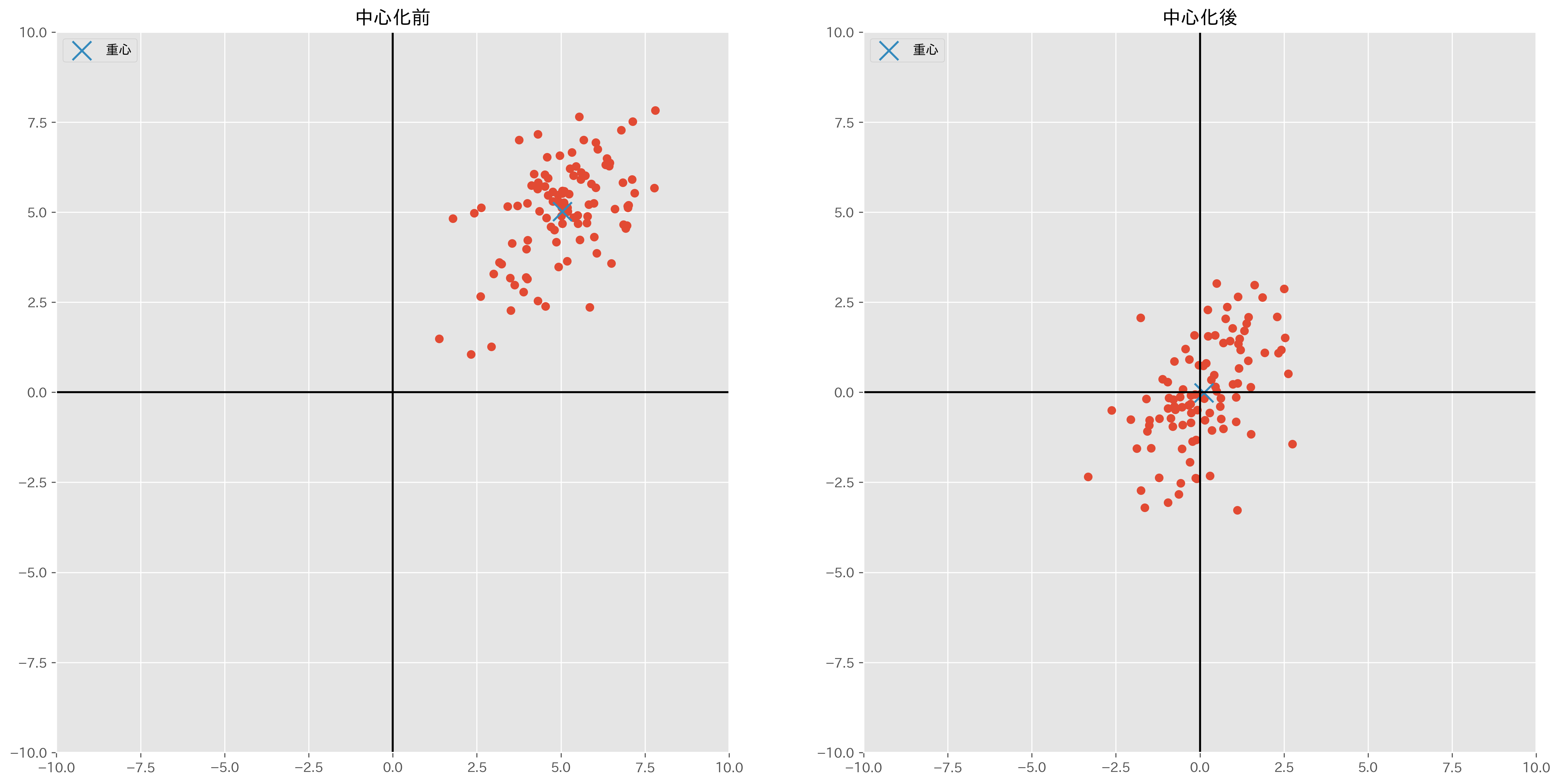
では、このデータの重心を原点に合わせるという操作にはどのようなメリットがあるのでしょうか?

データの重心からのズレを見るということは、データの分布の中心からの正味の変化を評価していることと解釈できます。^[1]

データの上がり下がりの傾向を見たいときに、データに平均が混ざってしまっていると分かりづらい。それならばいっそ中心化することによってデータから平均値を抜いてしまったほうがわかりやすいだろうという分析者の意図が見て取れます。

このように、共分散は統計学によって内積がツールとして洗練されたものなのです。

また、この中心化のメリットは相関係数が直線的な関係しか表さないことの説明にもつながってきます。

｢象限｣という概念は覚えているでしょうか?
象限とは下記の図のようにグラフをx軸とy軸によって4つのエリアに分ける考え方です。

この象限の考え方のポイントは、グラフ上の点がどの象限に属するかによってそのx、y成分の符号の組み合わせが異なるということです。

つまり、

• 第1象限、第4象限では、xとyが同符号になり、要素同士が類似した傾向を持つ点と言える。
• 第2象限、第3象限では、xとyは異符号になり、要素同士が逆傾向を持つ点と言える。

ということが、ポイントです。

中心化前のデータはすべての点が第1象限に属していますが、中心化後のデータでは、すべての象限にデータがあります。

このようにデータの象限を見るだけで数字同士の類似性がわかるようになることが中心化のメリットです。

共分散が中心化した個々の数字の傾向の類似性を足し合わせることで、データ全体の傾向の類似性を測る指標だということを思い出すと、第1象限、第4象限の点の分布度合いと第2象限、第3象限の点の分布度合いでデータ同士が同傾向なのか逆傾向なのかがパット見で評価できることがわかります。

ここまでの議論でわかったことを改めて整理すると共分散は以下のような指標だと言いかえることができます。

共分散とは、重心(平均)からの数値の上がり下がりの傾向を足し合わせた指標である。

ここで注目してほしいことは、あくまで共分散は数値の上がり下がりの傾向を見境なく足し合わせた指標であり、変化の傾向が途中から強くなったり、逆になったりするような傾向は無視するということです。

これはまさに、共分散が曲線的な変化の傾向を評価できず、直線的な傾向だけを表す指標であるということを意味しています。

相関係数は正規化した共分散だ

さあ、今までの議論でほとんど結論が出てしまったようにも見えますが相関係数がどうなるかを見てみましょう。

相関係数の定義を確認するところから始めましょう。

$$\displaystyle Corr(x, y) = \frac{Cov(x, y)}{\sqrt{V(x)}\sqrt{V(y)}}$$

($Cov(x, y)$: $x$と$y$の共分散、$V(x), V(y)$: $x$, $y$それぞれの分散)

つまり、相関係数は共分散を標準偏差の積で割ったものだと言うことがわかります。

ここでx,yが定数でない限り、標準偏差も必ず0よりも大きな数になるので、相関係数の分母も必ず正の数になることがわかります。(x, yが定数の場合、共分散も0になり無相関になるので考えないことにします。)

つまり、共分散から相関係数に変換したからと言って、符号が変化するということは起こり得ず共分散の解釈をそのまま適用してもOKということです。

相関係数の分母は、数字の範囲は-1 ~ +1の間に収めるための調整用の係数なので、解釈に影響を与えません。

なぜ、わざわざそんなことするのか?
念のため説明しておくと、
数字を-1~+1の範囲に収めることによって、数字の単位によらず他のデータ同士の相関係数と比較することが容易になるからです。

最後に

以上が、掛け算から理解する相関係数が直線的な関係しか表さないことに関する解説でした。

相関係数をより深く理解するための論点として、データが曲線的な関係にあった場合に相関係数の分母がどのような影響を生み出し、どのように変化していくかについて簡単なシュミレーションを通して理解を深めることも解説したいと思いましたが、力尽きたので別の機会にまとめようと思います。

まとめ

• 掛け算は2つの数字の傾向の類似性の尺度になる
• 内積は2つの数字の集合の傾向の類似性の尺度になる
• 共分散は、重心(平均)からの数値の上がり下がりの傾向を見境なく足し合わせた指標である
• 従って、曲線的な傾向を捉えることはできない
• 相関係数は共分散とほぼ同じなので、同じく曲線的な傾向を捉えることができない。

参考

「相関係数とは何か？」　を体系的に理解するための６ステップ - 主に言語とシステム開発に関して

「内積が見えると統計学も見える」第5回 プログラマのための数学勉強会 発表資料

象限とは？数学のグラフなどで出てくる必須知識｜高校生向け受験応援メディア「受験のミカタ」

脚注

1. 正規分布を前提としています