事例と実装で学ぶ因果推論〜ダイエットアプリの効果を検証するには?(第4回:傾向スコアマッチング)
こんにちは、Ubie Discoveryのmatsu-ryuです。
「事例と実装で学ぶ因果推論〜ダイエットアプリの効果を検証するには?」シリーズ4回目の記事になります。
前回は、「回帰モデル」について解説を行いました。
因果推論するための前提条件を満たし、線形モデルで生成した疑似データにおいて回帰モデルで効果検証できることを示しました。一方、回帰モデルの仮定を崩した疑似データにおいては、回帰モデルによる推定値が真の値からズレる状況を示しました。
今回は、このような状況にフレキシブルに対応できる「傾向スコアマッチング」について、解説していきます。
層別解析
傾向スコアマッチングの説明をする前に、層別解析について解説していきます。
- 層別解析での効果検証の方法を説明
↓ - 層別解析の限界
↓ - 傾向スコアマッチングの導入
という流れで説明していきます!
まずは、以下のような単純例を考えてみましょう
| ID | 年代 | 性別 | 食習慣 | アプリ利用 | 体重増減 |
|---|---|---|---|---|---|
| A1 | 50 | 男性 | 良い | 有り | -2 |
| B1 | 30 | 女性 | 普通 | 有り | -1 |
| C1 | 20 | 男性 | 良い | 有り | -4 |
| D1 | 60 | 男性 | 悪い | 有り | 0 |
| A0 | 50 | 男性 | 良い | 無し | -2 |
| B0 | 30 | 女性 | 普通 | 無し | -1 |
| C0 | 20 | 男性 | 良い | 無し | -4 |
| D0 | 60 | 男性 | 悪い | 無し | 0 |
真に知りたいことは、A1さんを例に取ると、
A1さんがアプリ利用した場合の体重増減 - A1さんがアプリ利用しない場合の体重増減
ですが、A1さんがアプリ利用しているので、アプリ利用しない場合の結果は観測できません。
そこで、A1さんと観測されている属性がほぼ同じで、アプリ利用していないA0さんの結果で置き換えよう、というのが層別解析の基本的な考え方です。(第2回の解説説明したExchangeblity)
上記のデータ例でいうと
で、アプリの利用効果が測定できます。
このような、マッチングする変数が少なく、変数のカテゴリ数が少ない場合は、層別解析でも問題ありません。しかし、以下のような問題があります
アプリ利用者とアプリ非利用者の背景情報をあわせるためにはより多くの変数でマッチングしたい
→変数が多くなるとマッチングする相手がいなくなる可能性がある
→ 第2回で解説した、Positivityの条件を満たさない
変数がカテゴリ変数ではなく、連続値の場合は、マッチングするレンジはどの程度にするべきか?
体重50kgは何キロの人までマッチングしてOKか?(52kg、54kg、56kg?)
そこで、複数の変数を圧縮して1変数で、アプリ利用群とアプリ非利用群をマッチングする術はないか?という発想が傾向スコアマッチングのアイディアの基本となります。
傾向スコアマッチング
複数の変数を圧縮してマッチングできるような変数ってどんな変数でしょうか?
観察データにおいては、アプリ利用者とアプリ非利用者の背景情報は、偏りがあるのが一般的です。(この偏りをなくすためにRCTを実施して効果検証するのでした)。言い換えれば、背景情報によって、アプリ利用する確率が異なるということです。であれば、この確率が同程度であれば、背景情報も同じような集団になるはずです。
疑似データの例を再掲して、傾向スコアマッチングによる効果検証の手順を示します。
疑似データを再掲します
- age:年齢
- gender:性別
- weight:体重
- diet:食習慣(0:良い、1:普通、2:悪い)
- treatment:アプリ利用有無
- outcome_0:アプリ利用無しの場合の体重増減(ポテンシャルアウトカム)
- outcome_1:アプリ利用有りの場合の体重増減(ポテンシャルアウトカム)
- outcome:実際に観測されたの体重増減
| ID | age | gender | weight | diet | treatment | outcome_0 | outcome_1 | outcome |
|---|---|---|---|---|---|---|---|---|
| A | 50 | Female | 77 | 2 | 1 | 3 | 3 | |
| B | 50 | Female | 77 | 2 | 0 | 5 | 5 | |
| C | 34 | Male | 57 | 1 | 0 | 2 | 2 | |
| D | 34 | Male | 57 | 1 | 1 | 0 | 0 |
1.傾向スコアモデルを作成
傾向スコアモデルは、2値分類モデルである必要があり、多くの場面で利用されるのはロジスティック回帰です。ロジスティック回帰の細かい解説は省きますが(1記事以上の内容になるので)、数式で表すと以下のようになります。
とすると
左辺
右辺は、シグモイド関数と呼ばれており、入力値を0から1の範囲に変換するため、確率として扱うことができます。
2.傾向スコアモデルから傾向スコアを求める
1で求めたモデルに個人ごとのXを入力することで
から傾向スコアを求めます。
3.アプリ利用群と同様傾向スコアを持つ人を、アプリ非利用群から選出(マッチング)
傾向スコアは連続量になるので、範囲を規定してマッチングします。
このマッチング方法には、
- 最近隣法マッチング
- 最適ペアマッチング
等があります。
最近隣法マッチングは個々のデータにおいて、傾向スコアが近いものを探しに行く方法で、集団全体として集団間の傾向スコアの距離が必ずしも最小とならない場合があるようです。集団での傾向スコアの距離が最小となることを目指す「最適ペアマッチング」を利用することが多いようです。
詳細は、統計的因果推論の理論と実装のP.161で解説されています。
4.マッチングしたデータにおいて、アプリ利用時の体重増減-アプリ非利用時の体重増減の平均を算出
上記の手順により、アプリ利用者におけるダイエットアプリの利用効果が推定できます。
これを、ATT(Average Treatment Effect on the Treated)といいます。後ほど詳しく説明します。
第3回の疑似データを傾向スコアマッチングで効果推定
ここから、前回「回帰モデル」では推定できなかったデータを利用して傾向スコアマッチングの実装例を解説していきます。
まずは、アプリ利用者における、真のダイエットアプリ利用の効果を求めてみましょう
# ATT
> data_1 <- data %>% filter(treatment==1)
> mean(data_1$true_effect)
[1] -5.885965
ということで、真の効果は、「-5.885965」ということがわかりました。
次に傾向スコアモデルを作成し、マッチングを実施しましょう。
マッチングに使用する変数は、疑似データの作成において体重増減に影響を与えている、体重(weight)、食習慣(diet)で行います。
(MatchItを利用すると、手順の1〜3が一括で実行できます。)
library(MatchIt)
m.out <- matchit(treatment ~ weight + diet, data=data, distance = 'glm', method = 'optimal')#optimalが最適ペアマッチングを意味します。
distance = 'glm':これで分類モデルにロジスティック回帰が実行されます。
method = 'optimal':最適ペアマッチングが実行されます。
一般的に分類モデルにおいては、分類の汎化性能を指標とする場合が多いですが、傾向スコアマッチングにおいては分類性能よりも、マッチング後の背景情報のバランシング結果を確認することが重要です。
マッチング後の背景情報(体重、食事習慣)のバランスがとれているかを確認してみましょう
library(cobalt)
love.plot(m.out, thresholds = .1)
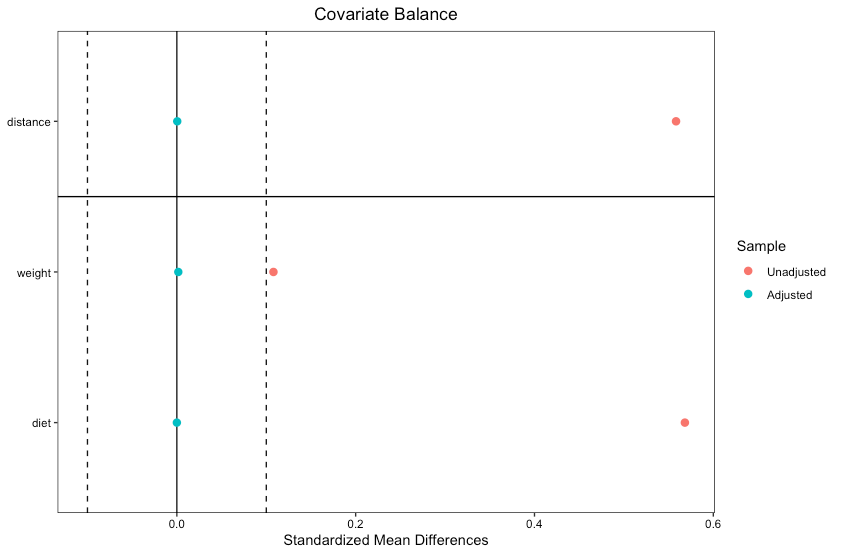
横軸に「標準化平均差」で、縦軸にバランシングに指定した変数の種類が並んでいます。
標準化平均差は、アプリ利用者群とアプリ非利用群の平均差を標準誤差で割った値となっています。
目安としては、この値が、+-0.1以内に収まるのが良いとされています。
赤丸がバランシング前で、青丸がバランシング後の値です。
マッチング前後のtableone集計も確認してみましょう。
- マッチング前
Stratified by treatment
0 1 p test
n 772 228
age (mean (SD)) 47.63 (13.94) 33.61 (11.04) <0.001
gender = Male (%) 341 (44.2) 148 (64.9) <0.001
weight (mean (SD)) 59.21 (11.31) 60.36 (10.60) 0.173
diet (%) <0.001
0 347 (44.9) 50 (21.9)
1 216 (28.0) 65 (28.5)
2 209 (27.1) 113 (49.6)
outcome (mean (SD)) 1.30 (2.97) -3.20 (1.80) <0.001
- マッチング後
# マッチング後のデータを作成
> m.data <- match.data(m.out)
> CreateTableOne(vars = vars, data = m.data, factorVars = c("gender", "diet"),
strata = c("treatment"))
Stratified by treatment
0 1 p test
n 228 228
age (mean (SD)) 48.24 (13.40) 33.61 (11.04) <0.001
gender = Male (%) 107 (46.9) 148 (64.9) <0.001
weight (mean (SD)) 60.34 (10.60) 60.36 (10.60) 0.986
diet (%) 1.000
0 50 (21.9) 50 (21.9)
1 65 (28.5) 65 (28.5)
2 113 (49.6) 113 (49.6)
outcome (mean (SD)) 2.68 (2.80) -3.20 (1.80) <0.001
マッチングで指定した、weight、dietは集団感で調整されています。
また、体重増減(outcom)の差は、-3.2-2.68=-5.88となり真の効果である「-5.885965」と同等の値が推定できています。
この推定は、以下の回帰式でも推定可能です。
> m.model <- lm(outcome ~ treatment, data = m.data, weights = weights)
> summary(m.model)
Call:
lm(formula = outcome ~ treatment, data = m.data, weights = weights)
Residuals:
Min 1Q Median 3Q Max
-6.8026 -0.8026 0.1974 1.1974 7.3158
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.6842 0.1557 17.24 <2e-16 ***
treatment -5.8816 0.2202 -26.71 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.351 on 454 degrees of freedom
Multiple R-squared: 0.6111, Adjusted R-squared: 0.6103
F-statistic: 713.5 on 1 and 454 DF, p-value: < 2.2e-16
なぜ、正しく推定できたか?
回帰モデルにおいては、体重の増減が、性別、年齢、体重、食習慣の変数の線形和であるという前提がありましたが、傾向スコアマッチングにおいては、この仮定は必要としません。
データの生成過程は、必ずしも線形関係とは限らないので、この仮定が緩和されることが傾向スコアマッチングを利用するメリットとなります。
ATT、ATC、ATE
先程も述べましたが、今回のダイエットアプリ効果の推定は、アプリ利用者群と同様の属性を持つ人をアプリ非利用者群からマッチングして行いました。
- マッチング前
Stratified by treatment
0 1 p test
n 772 228
・・・・
- マッチング後
Stratified by treatment
0 1 p test
n 228 228
・・・・
上記のとおり、treamtment=1(アプリ利用)の228人と同様の人をtreatment=0(アプリ非利用者)から、探してきている、という状況です。このように処置群(アプリ利用者群)における、効果推定値を
ATT(Average Treatment Effect on the Treated:処置群における平均処置効果)
といいます。ダイエットアプリの効果検証においては、「実際にアプリを利用した人のダイエット効果」になります。
逆に、treatment=0(アプリ非利用者)に対して、treamtment=1(アプリ利用)から同様の人を探して、効果推定値を求める場合もあります。このように対照群(アプリ非利用者群)における、効果推定値を
ATU(Average Treatment Effect on the Untreated:統制群における平均処置効果)
といいます。ダイエットアプリの効果検証においては、「まだアプリを利用していない人のダイエット効果」になります。
なお、第3回で解説した回帰モデルによる推定値は、集団全体における効果推定値となり、これを
ATE(Average Treatment Effect:平均処置効果)
といいます。(※ 回帰係数の傾きが、アプリ利用者群とアプリ非利用者群で共通という仮定の基)
このように、分析する手法によって推定する値が異なるので、「何を検証したいか?」目的を明らかにして検証する必要があります。
ダイエットアプリの効果検証を例にとると、
- 実際にアプリを利用した人の効果を推定したい場合:ATT
- まだアプリ利用していない人に対して、アプリ利用を促進して利用してもらった場合の効果を推定したい場合:ATU
といった感じになります。分析の目的を定めることが重要です!
次回
今回は、回帰モデルの前提条件を満たしていない疑似データに対して、傾向スコアマッチングの手法を用いることにより、アプリ利用者におけるダイエットアプリの利用効果が正しく推定できることを示しました。一方、集団全体における平均的な効果(=ATE)は、傾向スコアマッチングでは推定できません。傾向スコアを用いたもう一つの方法を利用してATEを推定する方法を学びます。次回のテーマは「IPW(Inverse Probability Weighting)」です!
一緒に働く仲間を探しています!
Ubie Discoveryは、「テクノロジーで適切な医療に導く」ことをミッションとしています。
このミッションをデータドリブンで実現することを目指しています。
そのためには、データアナリスト、アナリティクスエンジニア、データエンジニアの力が必要です。
そこで、私たちは一緒に働く仲間を募集しています!
興味のある方は下記JDから直接応募していただいても良いですし、一度カジュアルにお話したい方はそれぞれのメンバーと話せるカジュアル面談ページがあるのでぜひお気軽にご連絡ください。
最近soの制度もupdateされました。より魅力的なsoに生まれ変わってます!
Discussion