舵が切れなければ二輪車は倒れる(4) 固有値・固有ベクトルと挙動の関係

前回の記事では、舵角を$\delta=0$で固定した二輪車のロール方向の運動方程式

$$I_{Txx}\ddot{\phi} +m_Tz_Tg\phi = 0$$

の解が

$$\begin{align*} \phi(t) &= C_1 e^{\lambda_1t} + C_2 e^{\lambda_2t} \\ &= \Big(\frac{1}{2}\phi_0 + \frac{1}{2\sqrt{k}}\dot{\phi}_0\Big) e^{\sqrt{k}t} + \Big(\frac{1}{2}\phi_0 - \frac{1}{2\sqrt{k}}\dot{\phi}_0 \Big) e^{-\sqrt{k}t}, \;\; k = -\frac{m_Tz_Tg}{I_{Txx}} \end{align*}$$

として求まりました。

また、運動方程式を状態方程式に変換したときのシステム行列から求めた固有値・固有ベクトルが挙動の基本成分を表していることを紹介しました。このことを実際に数値を代入して計算することで確認してみたいと思います。

倒立振子の挙動シミュレーション

必要な諸元はMeijaardらの論文^[1]に記載されているものを利用して計算すると以下のようになりました。

$$\begin{align*} I_{Txx} &= 80.82\,\mathrm{kgm^2} \\ m_T &= 94.0\,\mathrm{kg},\: z_T = -0.8612\,\mathrm{m},\: g = 9.81\,\mathrm{m/s^2} \\ k &= 9.826\,\mathrm{s^{-2}} \end{align*}$$

よって固有値$\lambda_1,\:\lambda_2$と固有ベクトル$\boldsymbol{v_1},\:\boldsymbol{v_2}$は次のようになります。

$$\lambda_1 = 3.135, \:\boldsymbol{v_1} = \begin{bmatrix} 1 \\ 3.135 \end{bmatrix}, \;\;\; \lambda_2 = -3.135, \:\boldsymbol{v_2} = \begin{bmatrix} 1 \\ -3.135 \end{bmatrix}$$

ロール角の初期値を$\phi_0 = 1\,\mathrm{deg} = \pi/180\,\mathrm{rad}$、ロール角速度の初期値を$\dot{\phi}_0 = 0$として、

$$\begin{bmatrix} C_1 \\ C_2 \end{bmatrix} = \begin{bmatrix} \frac{1}{2}\phi_0 + \frac{1}{2\sqrt{k}} \dot{\phi}_0 \\ \frac{1}{2}\phi_0 - \frac{1}{2\sqrt{k}} \dot{\phi}_0 \end{bmatrix} = \begin{bmatrix} \pi/360 \\ \pi/360 \end{bmatrix}$$

を代入し、$t=0-1\,\mathrm{s}$についてグラフを描くと次のようになります。

ロール角が指数関数的に増加し、転倒していく様子が見て取れます。これは$\lambda_1$が正の実数であるためで、$C_1 e^{\lambda_1t}$の項は時間とともに増加していきます。一方$C_2e^{\lambda_2t}$の項は$\lambda_2$が負の実数であるため時間の増加とともに０に収束してきます。

挙動と固有値・固有ベクトルとの関係

前の記事で、物理空間でのロール角とロール角速度によるベクトル$\boldsymbol{\Phi} = [\phi\:\:\dot{\phi}]^T$は固有ベクトルを基底とするベクトル空間（モード空間）で表され、

$$\boldsymbol{\Phi} = \begin{bmatrix} \phi \\ \dot{\phi} \end{bmatrix} = C_1 e^{\lambda_1t} \boldsymbol{v_1} + C_2 e^{\lambda_2t} \boldsymbol{v_2}$$

となることを紹介しました。$\lambda_1$が正の実数、$\lambda_2$が負の実数であることから、$\boldsymbol{v_1}$の係数は指数関数的に増大し、$\boldsymbol{v_2}$の係数は０へ収束していくことから、時間の経過とともに$\boldsymbol{v_1}$成分が支配的になります。

横軸をロール角、縦軸をロール角速度としてグラフを描くと次のようになり、ロール角の増大とともに直線に近づき、その傾きが固有ベクトル$\boldsymbol{v_1}=[1\:\:3.135]$の傾き $3.135$ に漸近することが見て取れます。

一方、ゼロに収束していく固有値$\lambda_2$と固有ベクトル$\boldsymbol{v_2}$の組にはどのような意味があるのでしょうか。

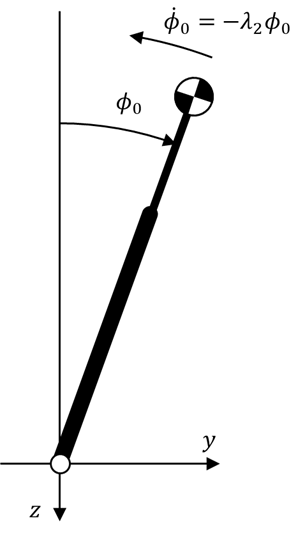
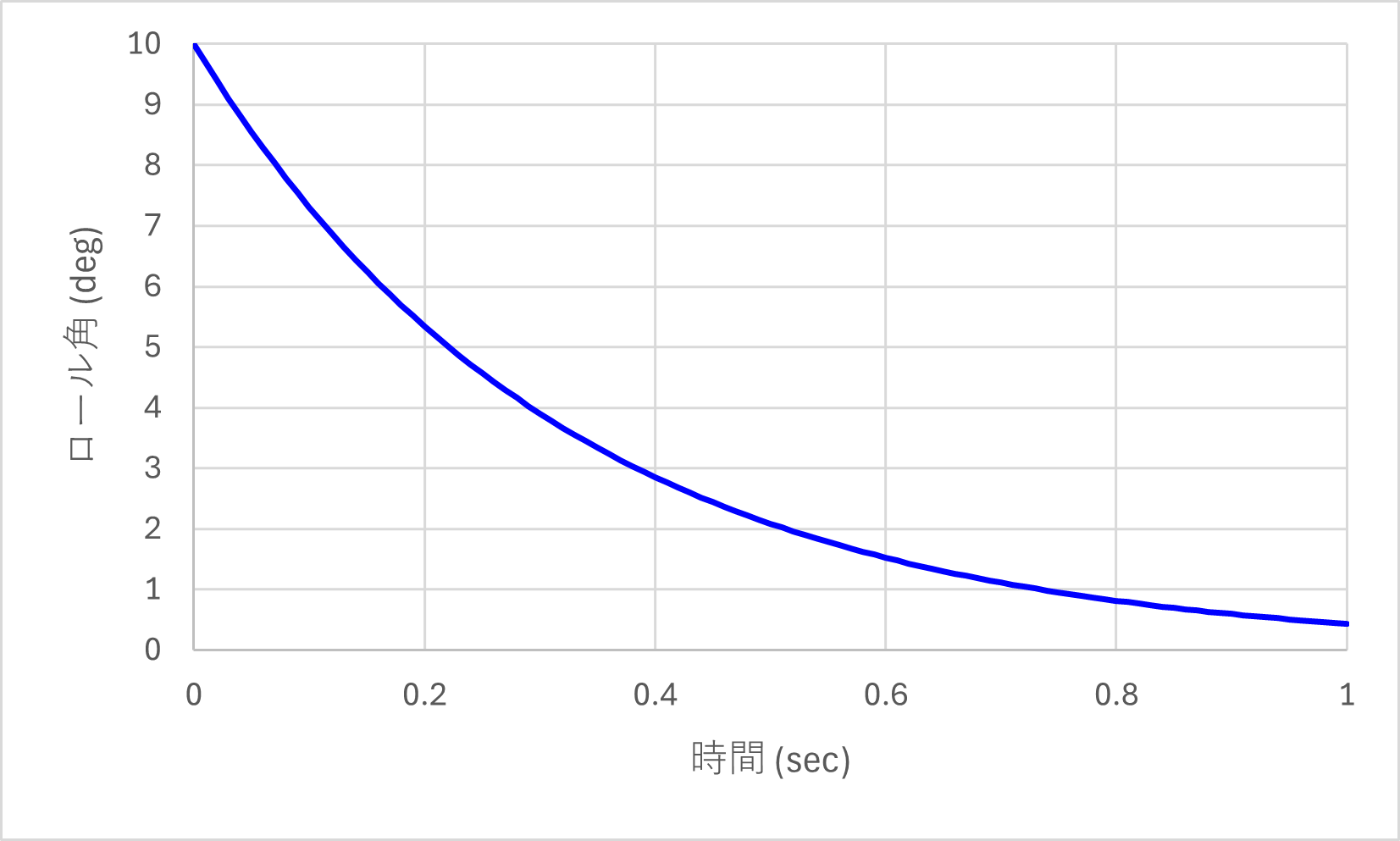
固有ベクトル$\boldsymbol{v_2}$も基底ベクトルの一つであるため、初期値のベクトルの方向ををこのベクトルに一致させると$C_2 e^{\lambda_2t}$の項が支配的となり、固有値が負の実数であることから０に収束していきます。ロール角の初期値を $\phi_0 = 10\,\mathrm{deg} = \pi/18$, ロール角速度の初期値を $\dot{\phi}_0 = -3.135*\pi/18$ としてグラフを描くと次のようにロール角は $\phi =0$ の直立状態に収束していきます。

つまり、ロール角とは逆向きの初速度を適切に与えることができれば倒れることなく直立状態に戻ることができるということを表しているのです。

初期状態	グラフ($\phi_0 = 10\,\mathrm{(deg)},\;\dot{\phi}_0 = -31.35\,\mathrm{(deg/s)}$)

このように固有値が負の実数であれば時間の経過とともに挙動が０に収束することから安定と呼ばれ、負の固有値の絶対値が減衰の程度を表すことから減衰率と呼ばれます。反対に正の実数の場合は増大・発散していくことから不安定と呼ばれ、機械や電気、制御などの設計では通常安定になるように設計検討がなされます。

また、各固有値に対応する固有ベクトルは固有モードとも呼ばれます。不安定な固有値がある場合その固有モードが表す挙動が支配的になるため、これも設計変更による対策の手がかりとして重要な指標となります。

固有値が虚数の場合

倒立振子の運動方程式に対して重力の符号を変えて上下を逆向きにすると単振り子になりますが、この場合は$k<0$となり固有値は虚数になります。そこで、$k'=-k$とおき、$\sqrt{k} = i\sqrt{k'}$を微分方程式の解の関数に代入すると、

$$\phi(t) = C_1 e^{i\sqrt{k'}t} + C_2 e^{-i\sqrt{k'}t}$$

となり、複素数の指数関数が表れます。この複素指数関数は三角関数に変換できることがわかっており、オイラーの公式として次の関係が成り立つことが広く知られています。

$$e^{i\theta} = \cos{\theta} + i\sin{\theta}$$

これを用いれば

$$\begin{align*} \phi(t) &= C_1 e^{i\sqrt{k'}t} + C_2 e^{-i\sqrt{k'}t} \\ &= C_1 (\cos{\sqrt{k'}t} + i\sin{\sqrt{k'}t}) + C_2 (\cos{\sqrt{k'}t} - i\sin{\sqrt{k'}t}) \\ &= (C_1 + C_2)\cos{\sqrt{k'}t} + (C_1 - C_2)i\sin{\sqrt{k'}t} \end{align*}$$

となり、

$$\begin{align*} C_1 + C_2 &= \phi_0 \\ C_1 - C_2 &= \frac{1}{\sqrt{k}}\dot{\phi}_0 = \frac{1}{i\sqrt{k'}}\dot{\phi}_0 \end{align*}$$

を代入すれば、

$$\phi(t) = \phi_0\cos{\sqrt{k'}t}+\frac{\dot{\phi}_0}{\sqrt{k'}}\sin{\sqrt{k'}t}$$

として三角関数で表すことができます。

更に、三角関数の合成公式を用いれば、

$$\phi(t) = \sqrt{\phi^2_0+\frac{\dot{\phi}^2_0}{k'}}\cos(\sqrt{k'}t - \beta), \;\; \beta = \tan^{-1}\frac{\dot{\phi}_0}{\phi_0\sqrt{k'}}$$

として表すことができ、単振動となっていることがわかります。

$\phi_0 = 10 \mathrm{(deg)}, \:\dot{\phi}_0 =0$としてグラフを描くと以下のようになります。

このように、固有値が虚数となる場合には振動することを表しており、この固有値の虚部（虚数単位の係数）$\sqrt{k'}$は振動の角速度表すことから固有角振動数と呼ばれます。

固有値が複素数の場合

上記の単振り子の支点に摩擦抵抗によって粘性減衰力が加わり、運動方程式には減衰項が加わって以下のように表せるものとします。

$$I_{Txx}\ddot{\phi} +c\dot{\phi} +m_Tz_Tg\phi = 0$$

この場合も同じように固有方程式を解いて固有値を求めると、

$$\lambda^2 + \frac{c}{I_{Txx}}\lambda + \frac{m_Tz_Tg}{I_{Txx}} = 0$$

$$\therefore \lambda = -\frac{c}{2I_{Txx}} \pm\sqrt{\Big(\frac{c}{2I_{Txx}}\Big)^2 - \frac{m_Tz_Tg}{I_{Txx}}}$$

となり、減衰係数 $c$ が小さいければ固有値は複素数となりなす。
そこで、$\lambda = -a \pm bi$とおいて微分方程式を解くと、解の関数は次のように求まります。

$$\phi(t) = e^{-at} \{ \phi_0\cos{bt} + \frac{1}{b}(a\phi_0 + \dot{\phi}_0)\sin{bt} \}$$

$c=50 \,\mathrm{(Nms/rad)}, \:\phi_0 = 10 \,\mathrm{(deg)}, \:\dot{\phi}_0 =0$としてグラフを描くと以下のようになります。

このように固有値が複素数の場合、指数関数と三角関数の積の関数となり、固有値が実数の場合や虚数の場合と同じように実部が減衰率を表し虚部が角固有振動数を表していることがわかります。

まとめ

運動方程式を変換して得られる状態方程式から、システム行列の固有値・固有ベクトルを求めることで、システムがどのようにふるまうかを知ることができます。

固有値の実部が負であればゼロに収束することから安定と呼び、正では発散するため不安定と呼びます。不安定な固有値が一つでもあれば発散する挙動が生じるため、通常は安定になるように設計します。
固有値が複素数の場合は虚部を角振動数とする振動が生じることを表しています。
また。固有値に対応する固有ベクトルは、固有値の表す時系列応答が生じる状態量の比を表します。

次の記事から、操舵系の運動も含む二輪車の運動方程式の固有値・固有ベクトルを求めることで、更に深堀したいと思います。

脚注

1. J. P. Meijaard, et al., "Linearized dynamics equations for the balance and steer of a bicycle: a benchmark and review", Proc. R. Soc. A 463:1955-1982, 2007