二輪車の運動特性(4) 二輪車はどうやって曲がるのか

これまで直進中の二輪車の運動方程式を基に、二輪車が倒れずに走ることができることをシステムの安定性によって説明してきました。

一方、旋回中の二輪車は遠心力やジャイロモーメントと重力とのバランスをとるために車体を傾けて走行することも紹介しましたが、それでも倒れずに走ることができるのが直感的には直進よりも更に難しいことのように感じます。しかし、実際の走行ではバランスを取ること自体に苦労することはなく、慣れてしまえば無意識に旋回できるようになることは、自転車に乗れる人には経験的にわかるでしょう。

ここでは、二輪車が旋回するにはどのように操縦すればよいか、またシステムの安定性とどのように関係しているのかを紹介したいと思います。

二輪車の旋回

一般に二輪車の旋回は逆操舵と呼ばれる特有の操縦方法によって行われているといわれています。直進から左へ旋回する過程を詳しくみていくと、

1. 操舵入力として右回りのステアリングトルクを加える
2. ハンドルが右に切れ、車体は左に傾く
3. セルフステアによってハンドルが左に切れて、左へ旋回する

といった挙動を示します。^[1][2]

このように、舵角やロール角に注目すると複雑な操縦をしているように見えるのですが、ライダーが入力している力である操舵トルクに着目すると実は非常に簡単な操作で旋回できることがわかっています。

旋回時の操舵入力

二輪車が安定となる必要条件として、定常旋回中の操舵トルクの向きは舵角と逆向きであることを前回の記事で紹介しましたが、直進から旋回に入るための逆操舵も曲がりたい方向とは逆向きに操舵トルクを加えていることがわかります。

つまり、安定な二輪車では旋回開始時から定常に至るまで常に曲がる方向とは逆向きの操舵トルクを加えていることになります。

一般に安定な制御系の過渡性能の評価にはステップ応答試験と呼ばれる評価方法が用いられ、階段状に変化する入力（ステップ入力）によって、入力直後の過渡応答や定常値への収束性能などが評価されます。

二輪車においても安定となる速度範囲では同様の評価を行うことができます。ベンチマーク自転車が安定である車速5m/sで直進走行している状態から、1秒後に-0.2Nmの操舵トルクがステップ上に入力されたときの挙動と軌跡を計算すると次のようになります。

右上のグラフが操舵トルクの時系列入力データで、計算開始から1秒後に-0.2Nmの操舵トルクが入力されていることが見て取れます。

右下のグラフはロール角と舵角の時系列応答データで、操舵トルクの入力直後には舵角は一旦曲がりたい方向とは逆向きに動いたあと、操舵トルクは変化しなくてもセルフステアによって自然に曲がりたい方向に切れていって一定値に収束していくことがわかります。

また、ロール角は自然に大きくなっていき、こちらも一定値に収束していきます。

左側のグラフは車両（後輪接地点）の軌跡を示していて、直進から定常旋回へと移行していく状態が見て取れます。操舵トルクが入力されるのは1秒後であり、x方向に5m進んだところから旋回に移るのですが、舵角は一旦少し左に切れたのちに右に切れていくため、更に5mほど進んだところから旋回を開始しているように見えます。このように二輪車はすぐには曲がれない特性を持っていますが、そのおかげで倒れずに走ることができるともいえます。

以上のように操舵トルクの大きさを調整すればロール角と舵角を同時に制御することができ、基本的には速度と曲率に合わせてロール角を制御すればライダーが思った方向に進むことができるという、シンプルな操縦方法が成立しています。

二輪車の安定性とステップ応答との関係

二輪車の安定性は運動方程式から得られるシステム行列の固有値実部によって評価でき、安定となる速度範囲があることを以前の記事で紹介しました。まず固有値解析の結果を再掲し、速度と固有値との関係を確認してみましょう。

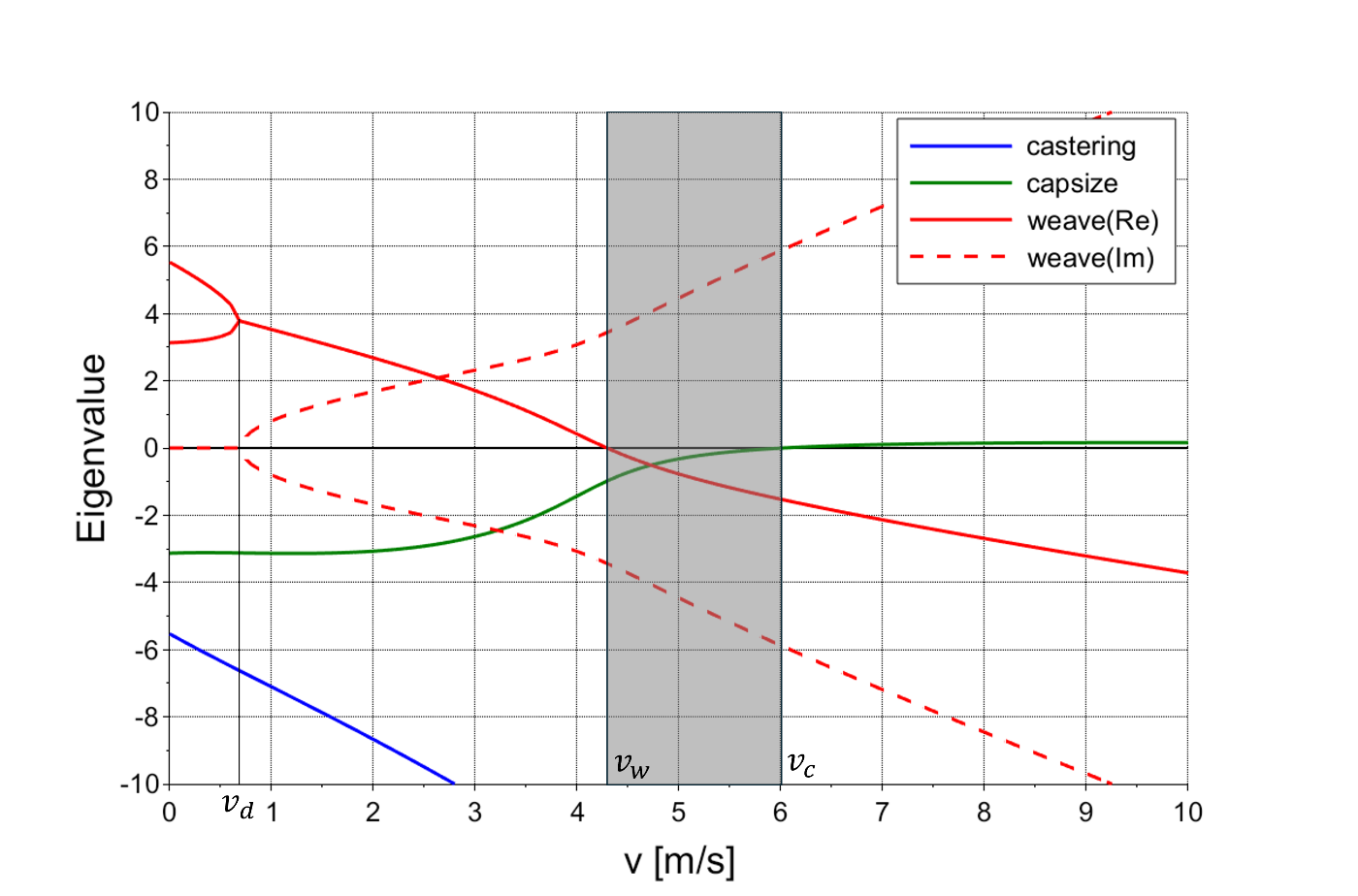
固有値の実部は実線で表されており、小さいほど安定であることを示しています。

先ほど示したのは車速5m/sでのステップ応答の結果でしたが、この速度ではどのモードも安定（固有値実部が負）であることがわかります。車速が低くなればキャプサイズモードが安定になる一方でウイーブモードが不安定になり、車速が上がるとその逆になっていることが見て取れます。

そこで、車速を変化させて時系列応答を見ることで、各モードの安定性がどのように挙動に影響するのか確認してみましょう。

まず車速4.5m/sでの結果です。

ウィーブモードが少し不安定になることで、ステップ入力直後のロール角と舵角の振動が収まりにくくなっているのがわかります。一方、キャプサイズモードは安定になることで、定常旋回への移行が早くなり、軌跡が綺麗な円を描くようになる一方、舵角もロール角も小さくなって旋回半径が大きくなっているのがわかります。

さらに速度を落として固有値実部が正となるとどうなるでしょうか。ここでは車速4.2m/sまで速度を落とした結果を示します。

ウイーブモードが時間とともに発散していき、ロール角・舵角とも振動しながら振幅が大きくなっていくとともに蛇行しているのがわかります。それでも定常旋回と同じように軌跡は円のまま蛇行しており、舵角やロール角の平均値はキャプサイズモードによって決まっていることが示唆されます。

では速度を上げて、ウイーブモードは安定に、キャプサイズモードが不安定になっていくとどうなるでしょうか。まず車速5.5m/sでの結果を示します。

ウイーブモードがより安定となったため、入力直後のロール角と舵角の振動はすぐに収まるようになっているのが確認できます。一方、キャプサイズモードの固有値は0に近づくことで、なかなか定常値に収束しなくなっており、ロール角・舵角ともに時間とともに大きくなってしまうことで軌跡も旋回半径が徐々に小さくなっていくのがわかります。

ではキャプサイズモードの固有値が正となり、不安定になるとどうなるのか、車速6.1m/sでの結果を示します。

キャプサイズモードが不安定になると、ロール角と舵角はもはや収束しなくなり、指数関数的に発散していくようになります。また、軌跡もどんどん旋回半径が小さくなっています。

ただし、この運動方程式はロール角・舵角ともに小さいものとして線形化されていることや、車輪と路面との間のタイヤ力は無限に発生するといった簡略化が行われているため、ロール角が30度を超える10秒以降の結果についてはあまりあてにならず、実際にはどこかで転倒することが予想されます。

また、キャプサイズモードが不安定で転倒するといった事例は現実には確認されておらず、ライダーが対処しているのではないかといわれていますが、このあたりは更なる調査が必要だと思います。

まとめ

二輪車が直進から旋回に移るときの挙動は一見複雑ですが、操舵トルク入力に着目すると非常に単純な入力で旋回できることがわかりました。

また、直進から旋回に移る挙動がウイーブモードとキャプサイズモードの安定性によって変化することを示しました。解析に使用したScilabスクリプトを末尾に添付しますので、興味のある方は固有値解析のスクリプト（benchmark_bicycleEIG.sce）を実行後、車速（27行目のv）や操舵トルク入力（7行目からはじまるstep_input(t)）などを変更して計算を実行してみてください。

以上のように、二輪車の安定性と操縦性に関する基礎的な知見について、解析手法とともに紹介してきました。これをもって第一部終了としたいと思います。

今後はこの解析のベースとして用いた運動方程式の導出方法とその限界や、より高速走行が可能なオートバイに特有な挙動への拡張などの紹介を計画しています。

benchmark_bicycleODE.sce

//================================================
// Step Response Analysis for the benchmark bicycle
// with Yaw angle expansion
//================================================
//
// Step input at t=1.0
function u = step_input(t)
    if t < 1 then
        u = [0; 0];
    else
        u = [0; -0.2];
    end
endfunction
//
// Bicycle Ordinary Differential Equation
function dq = BicycleODE(t,q,v,b,sl)
    u = step_input(t);
    dq = sl.A*q(1:4) + sl.B*u;
    dq(5) = v/b.w*cos(b.lambda)*q(2);
    dq(6) = v*cos(q(5));
    dq(7) = v*sin(q(5));
endfunction
//
// Main routine
//
// Step Response Calculation
v=5.5;
sl=BicycleSys(v,bicycle.g,M,K0,K2,C1);
//
t = 0:0.01:30;
q0 = [sl.X0; 0; 0; 0]
q = ode(q0, 0, t, list(BicycleODE,v,bicycle,sl));
// Data Plot
a=gda();
a.font_size=2;
a.title.font_size=4;
a.x_label.font_size=3;
a.y_label.font_size=3;
//clf();
f=scf();
f.axes_size=[1200 600];
// Trajectory
subplot(1,2,1);
plot(q(7,:),q(6,:));
replot([-10 -10 40 40]);
title("Vehicle Trajectory at speed = " +string(v) + " m/s");
xlabel("y position [m]");
ylabel("x position [m]");
xgrid();
a=gca();
a.x_ticks = tlist(["ticks" "locations", "labels"], -10:5:40, string(-10:5:40));
a.sub_ticks(1)=4;
// Steering Torque input
u_hist = zeros(t);
for i = 1:length(t)
    u_hist(i) = [0 1]*step_input(t(i));
end
subplot(3,2,2);
plot(t,u_hist);
replot([0 -0.3 30 0.1]);
title("Step Input for Steering Torque");
xlabel("Time [sec]");
ylabel("Torque [Nm]");
xgrid();
a=gca();
a.y_ticks = tlist(["ticks" "locations", "labels"], -0.3:0.1:0.1, string([-0.3 -0.2 -0.1 0.0 0.1]));
// Response of Roll and Steering Angles
subplot(2,2,4);
plot(t,q(1:2,:)*180/%pi);
replot([0 -5 30 30]);
title("Step Responses of Roll and Steering Angles");
xlabel("Time [sec]");
ylabel("Angle [deg]");
xgrid();
legend(['Roll';'Steering'],"in_lower_right");

脚注

1. みんなのモーターサイクル工学講座　運動のひみつ, 公益社団法人自動車技術会, ISBN978-4-904056-91-2, pp.79-81

2. 和歌山利宏, 図説バイク工学入門, グランプリ出版, ISBN978-4-87687-388-3, pp.27-28