Python Implementation of Bayesian Linear Regression Class

Introduction

I noticed that there are not many implementations of Bayesian linear regression with correct implementations, and there are few implementations that handle multi-dimensional inputs, so I implemented a user-friendly class. The description basically follows the PRML.

Implemented Class

To be honest, it's not a big implementation, it's only about 50 lines of code...
I'll write the entire class here. The features it has are as follows.
It's really simple.

• Calculate the posterior distribution given the combination of $\phi$ and $t$
• Perform random sampling of the mean and covariance parameters of Bayesian linear regression
• Output the mean and variance of the predictive distribution given $\phi$

Beyes_LR.py

import numpy as np
from scipy.stats import multivariate_normal

class BeyesLinearRegression:
    def __init__(self, mu, S, beta):
        self.mu = mu
        self.S = S
        self.beta = beta

    def calc_posterior(self, phi, t):
        S_inv = np.linalg.inv(self.S)

        if len(phi.shape) == 1:
            phi = phi.reshape(1, -1)
            t = t.reshape(1, 1)
        self.S = np.linalg.inv(S_inv + self.beta * phi.T @ phi)
        self.mu = self.S @ (S_inv @ self.mu + np.squeeze(self.beta * phi.T @ t))

    def sampling_params(self, n=1, random_state=0):
        np.random.seed(random_state)
        return np.random.multivariate_normal(self.mu, self.S, n)

    def probability(self, x):
        dist = multivariate_normal(mean=self.mu, cov=self.S)
        return dist.logpdf(x)

    def predict(self, phi):
        if len(phi.shape) == 1:
            phi = phi.reshape(1, -1)
        pred = np.array([self.mu.T @ _phi for _phi in phi])
        S_pred = np.array([(1 / self.beta) + _phi.T @ self.S @ _phi for _phi in phi])

        # Above is a simple implementation.
        # This may be better if you want speed.
        # pred = self.mu @ phi.T
        # S_pred = (1 / self.beta) + np.diag(phi @ self.S @ phi.T)
        return pred, S_pred

The entire code is also available on GitHub. (It's only about 50 lines)

GitHub

About Bayesian Linear Regression

I won't go into the details of the formula derivation, as the following references are more detailed on this.

• Implementing Bayesian Linear Regression in Python(Japanese)

• Regression using Bayesian Estimation(Japanese)

Calculation of Posterior Distribution

The important thing is that the distribution is updated as follows. In simple terms, $\phi$ is the explanatory variable and $t$ is the answer. Accordingly, the mean and covariance matrix are updated.

$$M_N=S_N(S_0^{-1}m_0+\beta\Phi^Tt)$$

$$S_N^{-1}=S_0^{-1}+\beta\Phi^T\Phi$$

Predictive Distribution

The predictive distribution is represented as follows. I'll skip the details here too, but the key point is that the distribution for a new point $x$ is represented by the following mean and variance.

$$N(m_N^T\phi(x), 1/\beta+\phi(x)^TS_N\phi(x))$$

Using the Implemented Class

From here, let's try Bayesian linear regression using the class I implemented.
The class I created requires you to provide the $\phi$ created from $x$. In a typical implementation, the part for generating $\phi$ (e.g. polynomials) is also incorporated into the class, making it unclear whether you are performing Bayesian linear regression or designing feature engineering using polynomials, but here I have separated them.

So, just input the original data $x$ and $y$, and then implement a function to create $\phi$, and that's basically it.

Regression on Sine Wave Data

Let's start with some toy data.

Data Generation and Feature Function Design

The input data is the true distribution of the sine wave with noise added as the observation data. As for the design of the feature function, it is a composite wave of several frequencies of trigonometric functions. The method x_to_phi vectorizes 10 waves, and _phi represents the composite wave. The amplitudes are the parameters to be estimated by Bayesian linear regression. Mathematically, it's like the image below. (Come to think of it, the first term is zero... it's not needed...)

$$y=w_1sin(0)+w_2sin(2\pi x)+w_3sin(2\times2\pi x)+\cdots+w_9sin(9\times2\pi x)$$

def x_to_phi(x):
    if len(x.shape) == 1:
        x = x.reshape(-1, 1)
    return np.concatenate([np.sin(2 * np.pi * x * m) for m in range(0, 10)], axis=1)


def _phi(x, params):
    return np.array([p * np.sin(2 * np.pi * x * i) for i, p in enumerate(params)]).sum(axis=0)

Here is the actual data generation part.

x = np.arange(0, 1, 0.01)
phi = x_to_phi(x)

e = np.random.randn(len(x)) / 10
y_true = np.sin(2 * np.pi * x)
y = y_true + e

Case of Observing Only One Point

First, let's consider the case where only the 50th data point is observed.

train_idx = 50
x_train = x[train_idx]
phi_train = phi[train_idx]
y_train = y[train_idx]
plt.scatter(x_train, y_train, c='crimson', marker='o', label='observation')
plt.plot(x, y_true, label='true')

Let's go ahead and calculate the posterior distribution for this data.
If you just want to learn, it's just one line like this.

# Initial values for Bayesian linear regression
input_dim = phi.shape[1]
mu = np.zeros(input_dim)
S = np.identity(input_dim)
sigma = 0.1
beta = 1.0 / (sigma ** 2)

# Model definition and training
beyes_linear_model = BeyesLR.BeyesLinearRegression(mu, S, beta)
beyes_linear_model.calc_posterior(phi_train, y_train)

I'll display the wave forms sampled randomly from the posterior distribution in green dotted lines, and the predictive distribution in light blue.
Since we only learned from one point, most of it is shown in blue.

Case of Observing 50 Points

Let's do exactly the same thing, but this time with 50 observation data points. The only difference in the code is that we randomly select 50 indices for train_idx.
The resulting predictive distribution is shown in the figure below.

Regression on Advertising Dataset

Next, let's solve a real-world problem, a multi-dimensional linear regression this time.
Since increasing the dimensionality by feature extraction would make it too hard to understand, I'll make $\phi$ a linear function.

Input Data

This is the famous Advertising dataset from ISLR.
This time, I'll use the TV and Radio advertising costs as input, and the sales as the response.

Since $\phi$ is linear this time, I just need to add an intercept term. The regression equation will be in the following form.

$$Sales = w_0+w_1TV+w_2Radio$$

def x_to_phi(x, typ='linear', degree=3):
    if len(x.shape) == 1:
        x = x.reshape(-1, 1)
    return np.concatenate([np.ones(x.shape[0]).reshape(-1, 1), x], axis=1)


df = pd.read_csv(ADVERTISING_DATASET)
x = df[['TV', 'Radio']].values
y = df['Sales'].values

phi = x_to_phi(x)
x_train, x_test, phi_train, phi_test, y_train, y_test = \
    train_test_split(x, phi, y, train_size=0.05, random_state=0)

All that's left is to train it the same way as before.

input_dim = phi.shape[1]
mu = np.zeros(input_dim)
S = np.identity(input_dim)
sigma = 10
beta = 1.0 / (sigma ** 2)

beyes_linear_model = BeyesLR.BeyesLinearRegression(mu, S, beta)
beyes_linear_model.calc_posterior(phi_train, y_train)

In the code, I set train_size to 0.05, but the regression planes drawn by changing this are shown below. I learned the Bayesian linear regression and extracted 5 planes by random sampling. When the number of training samples is small, nonsensical planes are drawn, but as the data points increase, it converges.

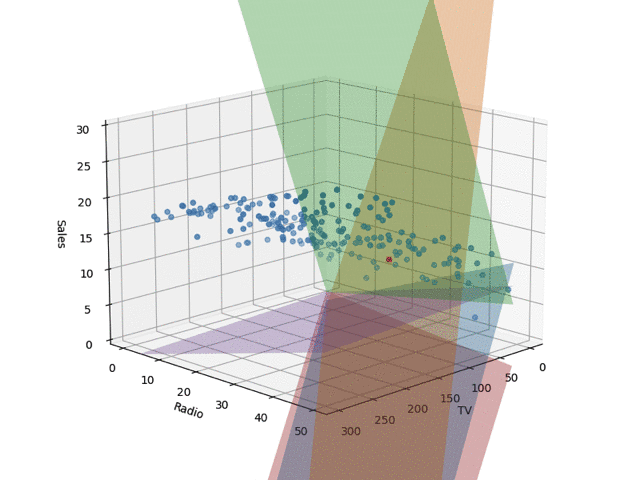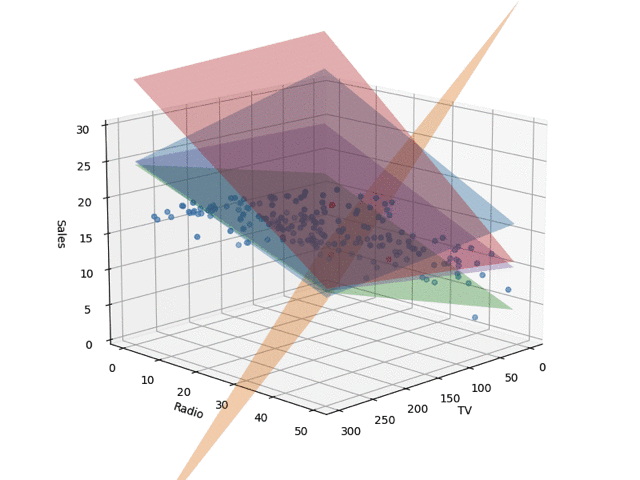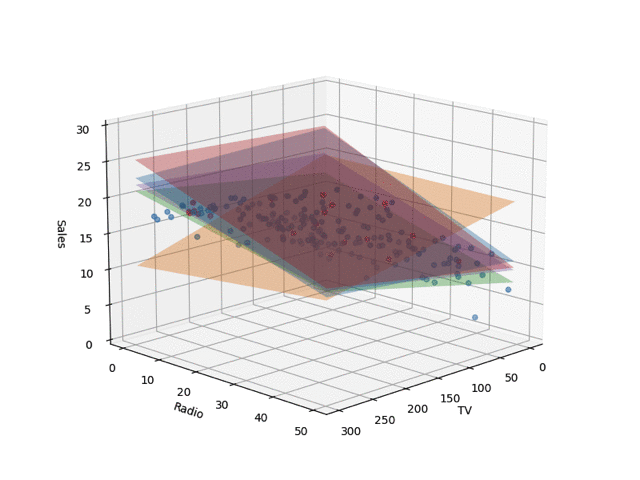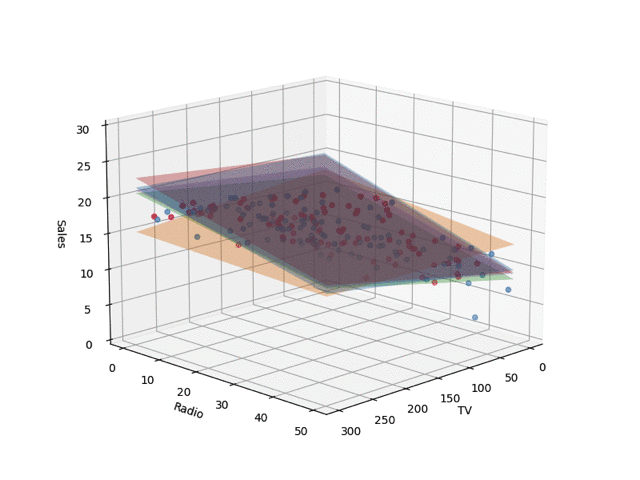
Conclusion

Finally, let me just briefly advertise Bayesian linear regression.
There are still parts that I don't fully understand, but the design of the feature extraction function $\phi$ in Bayesian linear regression becomes important. Handling the covariance matrix and using a kernel function as the design matrix is what Gaussian process regression is about, as I understand it.
However, if you have good prior knowledge to extract good features, Bayesian linear regression can often be sufficient, even from the perspective of interpretability. Also, Bayesian linear regression can do online learning right away due to its calculation method. You just need to use the posterior distribution you calculated as the prior distribution for the next learning. You don't even need to recalculate the Gram matrix like in Gaussian process regression. There are online versions, but...

Well then, I hope you enjoy a comfortable Bayesian linear regression life!

This article has been translated by a generative AI from the original Japanese text.