SCCL:対照学習の応用による文書クラスタリング
はじめに
こんにちは。今回は、こちらのSCCL(Supporting Clustering with Contrastive Learning)という新しいクラスタリング手法について記述します。
Supporting Clustering with Contrastive Learning
※本記事にある画像や数式は、当論文より引用しています。
Contrastive Learningは対照学習のことです。正直なところ、対照学習については学び始めたばかりの段階です。ですが、ここ最近画像処理の分野で著名な対照学習が自然言語処理に応用されていることに興味を持ちました。それで、今回知って読んだ論文を記事に起こすことにしました。
今回の記事は特に理論面の記述の割合が高いので、いきなり細部まで理解しようとせずに読んでいただけたらと思います。
クラスタリングについて
クラスタリングの要件
当たり前かもしれませんが、クラスタリングはただ複数のクラスターを作れればいいというものではないです。望ましいのは、作成した各クラスターが、他のクラスターとは異なる何かしらの特徴やカテゴリを持っていることです。
これまでのクラスタリングの手法
通常、クラスタリングの際には、あらかじめ各データを特徴量ベクトルにしておいて、各特徴量ベクトルを用います。
傾向として、各データの特徴量ベクトルの次元が大きすぎると、クラスタリングがうまくできなくなります。これは以前も少し触れた、次元の呪いの一種です。
そこで、近年の様々な深層学習モデルを利用する手があります。これで、なるべく各データの情報を保ちながら、ほどほどの次元の特徴量ベクトルが得られます。そうすることで、クラスタリングがよりうまくいくようになります。
課題
そうは言っても、本質的に違うもの同士の特徴量ベクトルが接近してしまう場合があります。そうなると、それらのデータは同じクラスターに入ってしまう可能性が高くなります。
うまくクラスタリングするには
それではどうすればよいか。何らかの工夫により、カテゴリの異なるデータ同士の特徴量ベクトルが接近していない状況を作るのが一策です。そうすれば、異なるデータ同士が同じクラスターに入ってしまう可能性を減らせます。
SCCLでは、そういうことができるようになっています。
SCCLによるクラスタリング
ここからSCCLの話に入ります。
SOTAの達成
Papers with CodeのShort Text Clusteringタスクはあまり盛り上がっていませんが、それでもほとんどのベンチマークにてSCCLがSOTAになっています。
https://paperswithcode.com/task/short-text-clustering
SCCLの全体像
全体像は次の通りです。

詳しくは、これから説明していきます。ただひとまずおさえておきたいのは、各データをベクトル化(上の図でいうと中央のψ)したものに、さらに変換をかけていくことです。その変換とは、上の図でいうと一番右の変換f、gのことです。目指すのは、最適なf、gを求めることです。
従来は、中央のψでデータをベクトル化したものをそのままクラスタリングにかけるのが定番でした。それに対してSCCLでは、さらに変換をしてからクラスタリングにかけるわけです。
f、gの最適化の手順
最適なf、gを求めるための大まかな手順は、次の1~4の繰り返しになります。
- データセットからランダムにM個のデータを選ぶ。これをミニバッチとする。
- ミニバッチ内のM個の各データごとに、何かしらの手法によりデータ拡張を行い、1件のデータを生成する。生成したものはミニバッチに加える(これで、ミニバッチ内のデータ数は2Mとなる)。
- 何か深層学習モデルなどを用いて、ミニバッチ内の各データをベクトル化する。
- ある損失関数の値が最小になるように、変換f、gを更新する。
1から3まではともかく、4が肝です。
損失関数の構成
上の4で書いた損失関数は、下の式のように大きく2つから成ります。それら2つは、「instance-CL損失」というものと、「クラスター損失」というものです。
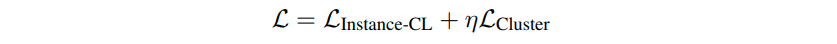
ηは、両者のバランスを取るためのハイパーパラメータです。ここでは値として10を設定しています。
instance-CL損失
instanceは1データのことです。CLは対照学習です。CLと書くとクラスタリングみたいに見えますが、クラスタリングではなく対象学習です。
対照学習については予備知識があると理解しやすいですが、予備知識がなくてもなるべく理解できるように説明を書いてみます。
データごとのCL損失の定義
前述のように、この時点でミニバッチ内のデータは2M個あります。これら2M個の各データごとに、CL損失というものが計算されます。式は次のようになります。

左辺の添え字のi1(iの1乗みたいな表記)は、ミニバッチ内の1つのデータです。つまり、この式の右辺はデータi1についてのCL損失を意味します。
i1に対してi2は、i1とのペアを成すデータです。いわば、i1の相方です。たとえばi1はあるオリジナルのデータなら、i2はそのデータを元にして生成されたデータのことです。逆にi1は生成されたデータなら、i2は生成元のオリジナルのデータのことです。
各zは、ψによって特徴量ベクトル(特徴量表現)になったものを、gで変換したものです。
simは類似度(similarity)です。ここでは、先行研究にならってコサイン類似度となっています。類似度が高いほど、お互いのデータの特徴量ベクトルは近いことになります。
1は指示関数(添えられている式が正しいなら1、正しくないなら0をとる関数)です。
τ(タウ)は温度パラメータと呼ばれるものであり、ハイパーパラメータの一種です。ちなみに、具体的な値として0.5を設定しているようです。
CL損失の定義の解釈
この式を解釈してみます。
対数関数内の分子は、ざっくり言えばi1とその相方i2の類似度です(正確に言えば、τやexpもありますが)。分母は、i1と各データの類似度の和です(ただし、i1自身との類似度は除きます)。分母は変形すれば、「分子の式」+「i1と他の各ペアの各データの類似度の和」となります。
簡素ですが、図解するとこのようになります。

各丸は、ミニバッチ内の1つのデータです。同じ色同士はペアです。★付きのデータは、CL損失の計算の対象のデータです。
上の式の分子は、上の図の黒い線でつなげられた2つのデータの類似度です。分母はそれに加えて、各グレーの線についての類似度の和を追加したものです。
以上を踏まえると、CL損失の値を小さくする変換gの採用により、異なるデータ同士があまり接近していない状態を作ることができます。
クラスター損失
全体の損失関数のうちもう1つの要素は、クラスター損失です。
いったんここでは、データは各オリジナルデータに限定します(つまり、データ拡張により生成した各データは考慮外)。また、クラスターの数をKとします。
ここで用いられるクラスタリングの仕組み自体は、混合ガウスモデルとそんなに変わらないです。より具体的には、混合ガウスモデルにおいて各クラスターの持つ確率分布であるガウス分布(正規分布)を、t分布に置き換えたものです。また、各確率分布の分散は、クラスターによらず一定としています(なので、各クラスターの大きさは同じくらいになりやすいです)。これらの仮定は、後述のqの式に反映されています。
データごとのクラスター損失の定義
このクラスター損失は、各データごとのクラスター損失の和です。データjのクラスター損失は、次の式で表されます。

KLは、カルバック・ライブラー情報量です。これはある意味、2つの入力内容の間の距離みたいなものです。両者が異なっている場合ほど、カルバック・ライブラー情報量は大きくなります。
qの式はこちらです。

このqの式の解釈としては、「データjがクラスターkに属する確率」となります。
縦棒2つで囲って右下に2の添え字が付くものは、L2ノルムです。これは、中身のベクトルの長さに相当します。その右上についている2は、単に二乗のことです。なので、L2ノルムの二乗になります。
eは、(データjの)特徴量表現です。μは、k番目のクラスターの中心点です。
αはハイパーパラメータで、ここではα=1を設定しています。
pの式はこちらです。pの中にあるf_k(変換fのことではない)の定義は、pの式のすぐ下にあります。ひとつの見方として、これはqの二乗の加重平均と言えます。
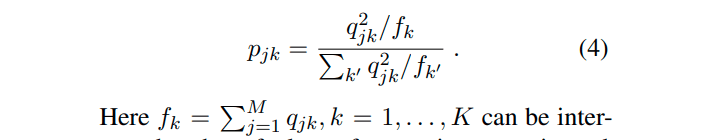
また、変換fが明示的に出てこないので補足しておきます。変換fは、特徴量ベクトル(ψによる得られるもの)をK次元のベクトルに変換します。この出力のベクトルの各成分は、上の各qのことです。そうなると、何を最適化すればよいのかという疑問が浮かびます。具体的には、各クラスターに対する中心点μになると思います。各μをうまく調整することで、クラスター損失を下げていきます。
クラスター損失の定義の解釈
もし、pの式にあるqの二乗が単にqであり、またkによらずfが一定の値なら、pとqは同じです。クラスター損失の定義がpとqのカルバック・ライブラー情報量になっている以上、pとqが同じでは意味がありません。ですので、この定義には相応の意義があると考えます。
具体的に言えば、まずqの二乗となっていることにより、qの値が大きくなりすぎたり小さくなりすぎたりするのをうまく抑制していると思います。qの値が大きすぎ(あるいは小さすぎ)だと、(同じkに対応する)pが相対的にさらに大きすぎ(あるいは小さすぎ)になって、qがpから離れやすくなるからです。そうなると、損失が大きくなってしまいます。逆に言えば、損失を抑えるためには、各qはほどほどの値(理想的には1/K)である必要があるということです。
各qの値がほどほどであれば、各クラスターに対する所属確率は同じくらいになるので、クラスタリングの観点からすれば好ましいと言えます。
また、各f_kに差があると、あるクラスターは中心点が全体的に各データに近く、逆に他のクラスターは中心点が全体的に各データから遠いことになります。こうなってはクラスター間で不平等となり、あまり良いこととは言えないです。
各f_kに差があると、分子であるqの二乗に影響し、それによってpとqの乖離が起きやすくなってしまうと思います。逆に言えば、このfがあることで、pとqの乖離を抑制していると思います。
各データはどのクラスターに入ることになるか
変換f、gを最適化したあと、各オリジナルのデータはどのクラスターに入ることになるか。答えは、そのデータを変換ψ、さらに変換fによって各クラスターへの所属確率qを求めた際の、所属確率qの最も高いクラスターです。
ちなみに今回の場合は、所属確率qの最も高いクラスターは、中心点がそのデータから最も近いクラスターでもあります。なぜなら、各クラスターの持つ確率分布は、中心点を除いて同一だからです。
SCCLについての考察
SCCLについて、自分なりの考察を述べてみます。
SCCLなら、確かにカテゴリの異なるデータ同士は接近しにくくなる気がします。CL損失に基づく最適化後のfによって、各オリジナルデータを変換します。そうすると、想像ですが、データの散らばりぐあいが均一になりやすいと思います(特定の領域にデータが密集しにくいということ)。
なぜなら、最適化されたfにより、互いに異なるデータ同士はなるべく離されるはずだからです。もちろんデータの組ごとに離しぐあいに差があると、相対的に密度の高い領域は発生しやすいかもしれません。しかしそれは、クラスター損失のおかげで防がれているように思います。
データの散らばりぐあいが均一であるということは、接近しているデータ同士が少ないということ。ですので、カテゴリの異なるデータ同士が同じクラスターに入ってしまう可能性が下がることになると思います。
加えて、データの散らばりぐあいが均一だと、特定のクラスターの肥大化が起こりにくそうです。これも、クラスター損失がうまく働いているからだと思います。
実験
以下に示す通り、既存のクラスタリング手法のスコアを超える結果が得られました。
各変換に用いるモデル
最初に各データを特徴量ベクトルにする際には、Sentence-transformerのモデルが用いられています。具体的には、Hugging Faceにアップされたこのモデルです。
https://huggingface.co/sentence-transformers/distilbert-base-nli-stsb-mean-tokens
CL損失向けの変換gには、多層パーセプトロンモデルが用いられています。このモデルは、次元数768の隠れ層を1層持ち、128次元のベクトルを出力するモデルのようです。
データセット
データセットは次の通りです。

結果
結果は次の通りです。
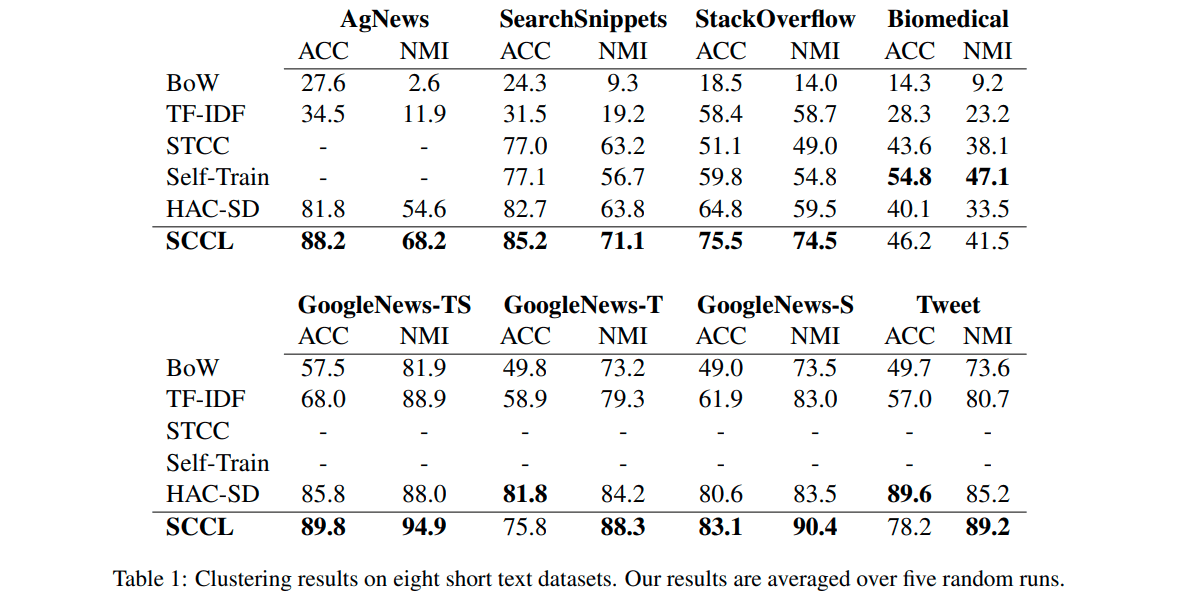
ACCは正解率、NMIはNormalized Mutual Informationです。
STCCやHAC-SDなどはクラスタリング手法です(ちなみに、BoWやtf-idfがありますが、ここではベクトル化したものをk-meansでクラスタリングする手法のようです。各手法の詳細は、当論文をご参照ください)。
見ての通り、今回のSCCLが他の手法のスコアを超えていることが分かります。
今回の手法に限らず、1つの実験だけで性能について安易に断じるのは良くありませんが、これでSCCLの強みを実感できた気がします。
補足(データ拡張の手法について)
データ拡張の手法も興味深いところなので、簡単に記述しておきます。ただ、詳細は分かりかねるところがありますので、詳しくは当論文をご参照ください。
実験では、3種類の方法が試されました。特に有益だった方法は、データの文章の中から単語をいくつか探索し、それらを別の単語に置き換える方法です。あるいは、新たに単語を文中のどこかに挿入することです。この手法には、事前学習済みのtransformerモデルが用いられたようです。
終わりに
最後までお読みいただき、ありがとうございました。
Discussion