【C++】流体の流れ可視化するシミュレーション解析

流体に関する方程式
1.Navier-Stokes方程式(NS方程式)
流体力学ではとても有名な式かと思います。
左辺の第二項が慣性項、
右辺の第一項が粘性項、
右辺の第二項が圧力項、
右辺の第三項が外力項(体積項(浮力)のみ考慮)
となっています。
ちなみに、今回は積分形式で表しております。
この数式は一般解を未だに解くことが出来ていない、
ミレニアム検証問題
としても有名ですね。
数学的解くことができれば、
懸賞金100万ドルを手にすることができるそうです。
(数学得意な方、チャンスです!)
ただ物理的には、
近似解を求めることが出来ることが知られており、
私は物理屋なので、
数学的には解けないものを、
離散化すれば数値を出すことができるのが物理の強み
だなと、日々思っております。
2.連続の式
こちらも、
流体力学ではとても有名な式かと思います。
NS方程式と同様に積分形式で表しています。
それでは、
この2式を頼りにして、コードを作成していきます。
解析条件
- 2次元キャビティー流れの解析
- MAC法(Marker And Cell method)を採用
- 中心差分法を採用
- 解析対象のサイズはX方向1m、Y方向1m
- 上部の壁は右へ速さ1mで移動
- 節点数は51×51、セル数は50×50
- レイノルズ数は100
- 解析刻みは0.001秒、20秒で解析終了
といった感じで解いてみようかと思います。
C++でコードを書く
早速、コードを書いてみようと思います。
速度の境界条件は以下のようにしました。
//境界条件(左右)
for(j=0;j<yn+1;j++)
{
u[1][j]=0.0;
u[0][j]=u[2][j];
v[0][j]=-v[1][j];
u[xn][j]=0.0;
u[xn+1][j]=u[xn-1][j];
v[xn][j]=-v[xn-1][j];
}
v[0][yn+1]=-v[1][yn+1];
v[xn][yn+1]=-v[xn-1][yn+1];
//境界条件(上下)
for(i=0;i<xn+1;i++)
{
v[i][1]=0.0;
v[i][0]=v[i][2];
u[i][0]=-u[i][1];
v[i][yn]=0.0;
v[i][yn+1]=v[i][yn-1];
u[i][yn]=2.0*uwall-u[i][yn-1];
}
u[xn+1][0]=-u[xn][0];
u[xn+1][yn]=-u[xn][yn];
ここでポアソン方程式を解きます。
//ポアソン方程式を解く
for(k=1;k<=km;k++)
{
err=0.0;
//圧力に関する境界条件
for(j=0;j<yn+1;j++)
{
p[0][j]=p[1][j]-1.0/re*2.0*u[2][j];
p[xn][j]=p[xn-1][j]+1.0/re*2.0*u[xn-1][j];
}
for(i=0;i<xn+1;i++)
{
p[i][0]=p[i][1]-1.0/re*2.0*v[i][2];
p[i][yn]=p[i][yn-1]+1.0/re*2.0*v[i][yn-1];
}
//SORによる収斂計算//
for(i=1;i<xn;i++)
{
for(j=1;j<yn;j++)
{
pres=C1*(p[i+1][j]+p[i-1][j])+C2*(p[i][j+1]+p[i][j-1])-C3*r[i][j]-p[i][j];
err+=pres*pres;
p[i][j]=pres+p[i][j];
}
}
if(err<=0.000005) break;
}
これで、各メッシュの圧力を求めることができます。
この結果を用いて、
各メッシュの速度の値を更新していきます。
//X方向速度の算出
for(i=2;i<xn;i++)
{
for(j=1;j<yn;j++)
{
vmid=(v[i][j]+v[i][j+1]+v[i-1][j+1]+v[i-1][j])/4.0;
uad=u[i][j]*(u[i+1][j]-u[i-1][j])/2.0/dx+vmid*(u[i][j+1]-u[i][j-1])/2.0/dy;
udif=(u[i+1][j]-2.0*u[i][j]+u[i-1][j])/dx/dx+(u[i][j+1]-2.0*u[i][j]+u[i][j-1])/dy/dy;
u[i][j]=u[i][j]+dt*(-uad-(p[i][j]-p[i-1][j])/dx+1.0/re*udif);
}
}
//Y方向速度の算出
for(i=1;i<xn;i++)
{
for(j=2;j<yn;j++)
{
umid=(u[i][j]+u[i+1][j]+u[i+1][j-1]+u[i][j-1])/4.0;
vad=umid*(v[i+1][j]-v[i-1][j])/2.0/dx+v[i][j]*(v[i][j+1]-v[i][j-1])/2.0/dy;
vdif=(v[i+1][j]-2.0*v[i][j]+v[i-1][j])/dx/dx+(v[i][j+1]-2.0*v[i][j]+v[i][j-1])/dy/dy;
v[i][j]=v[i][j]+dt*(-vad-(p[i][j]-p[i][j-1])/dy+1.0/re*vdif);
}
}
これを解くことで、
0.001秒ごとの各メッシュの流体の速度を
知ることができます。
解析結果
今回作ったモデルでの解析結果を以下に記します。
赤矢印が流体の速度ベクトルになります。
解析から0.005秒後

解析から0.05秒後
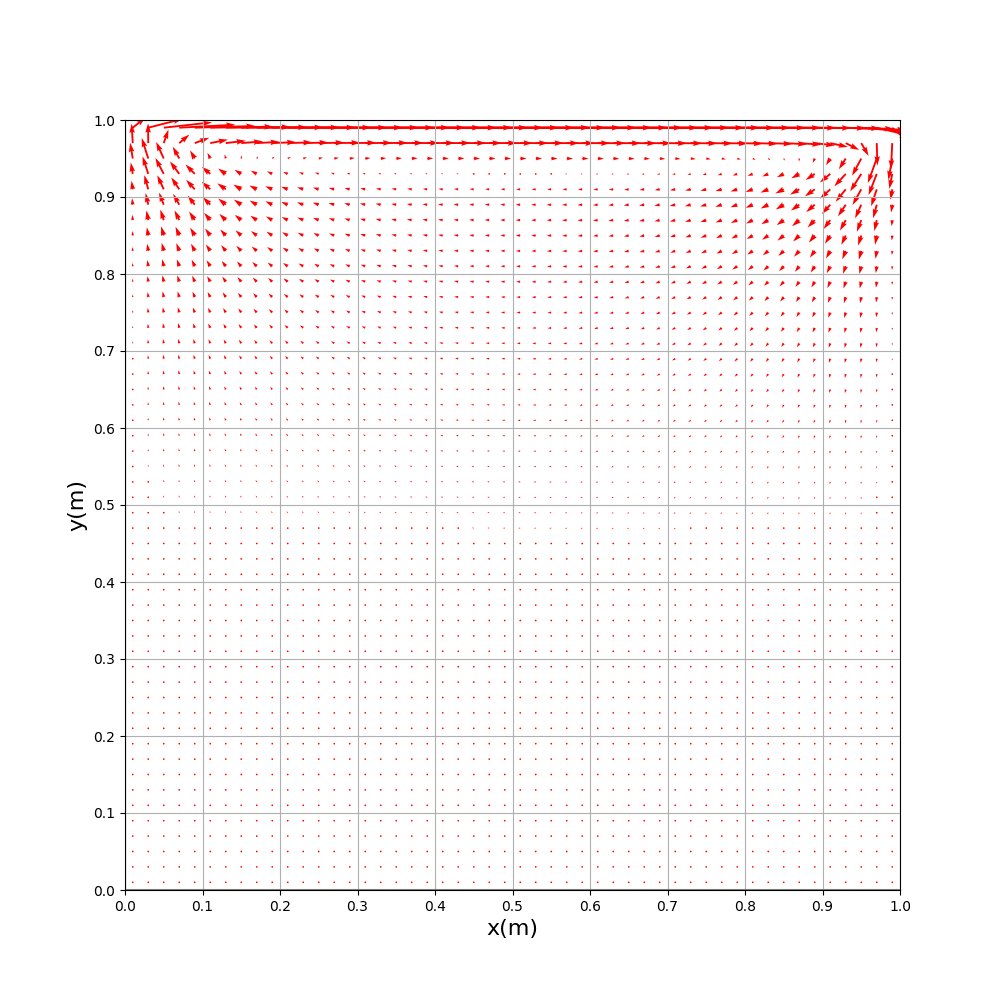
解析から0.5秒後
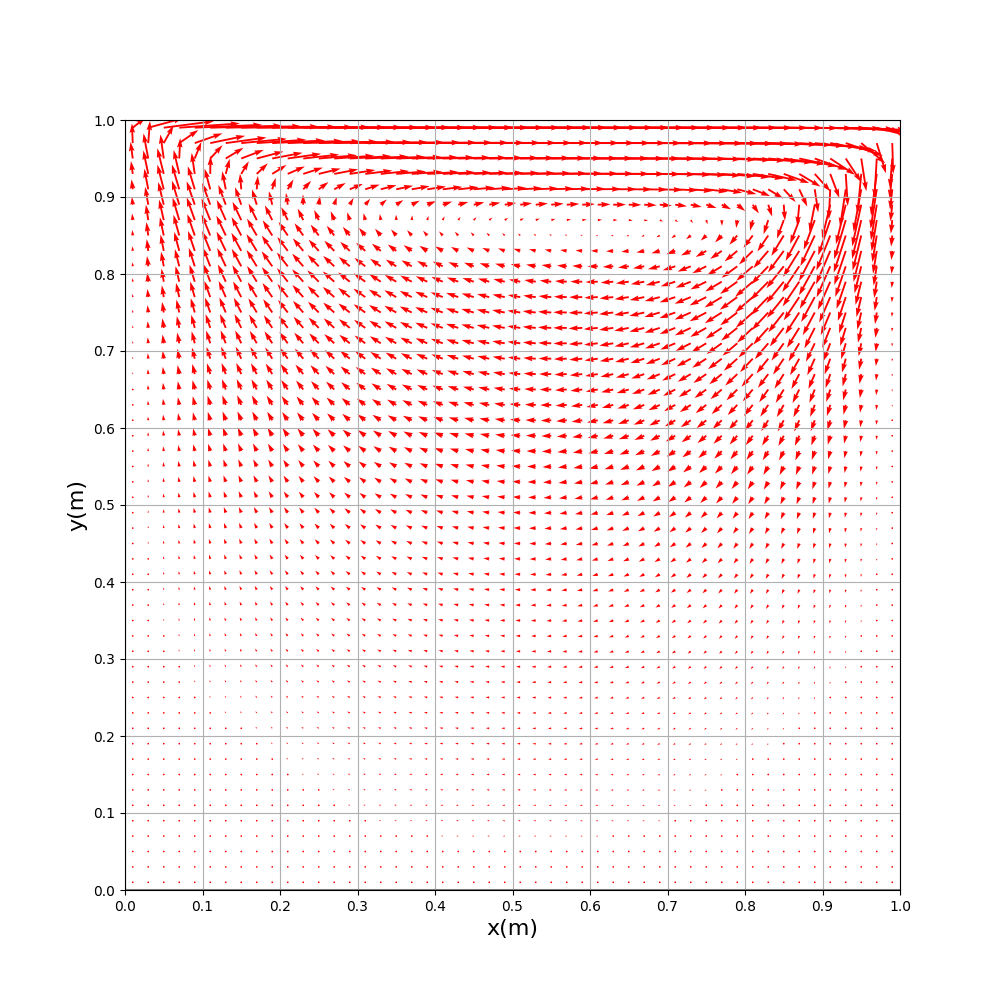
解析から5.0秒後
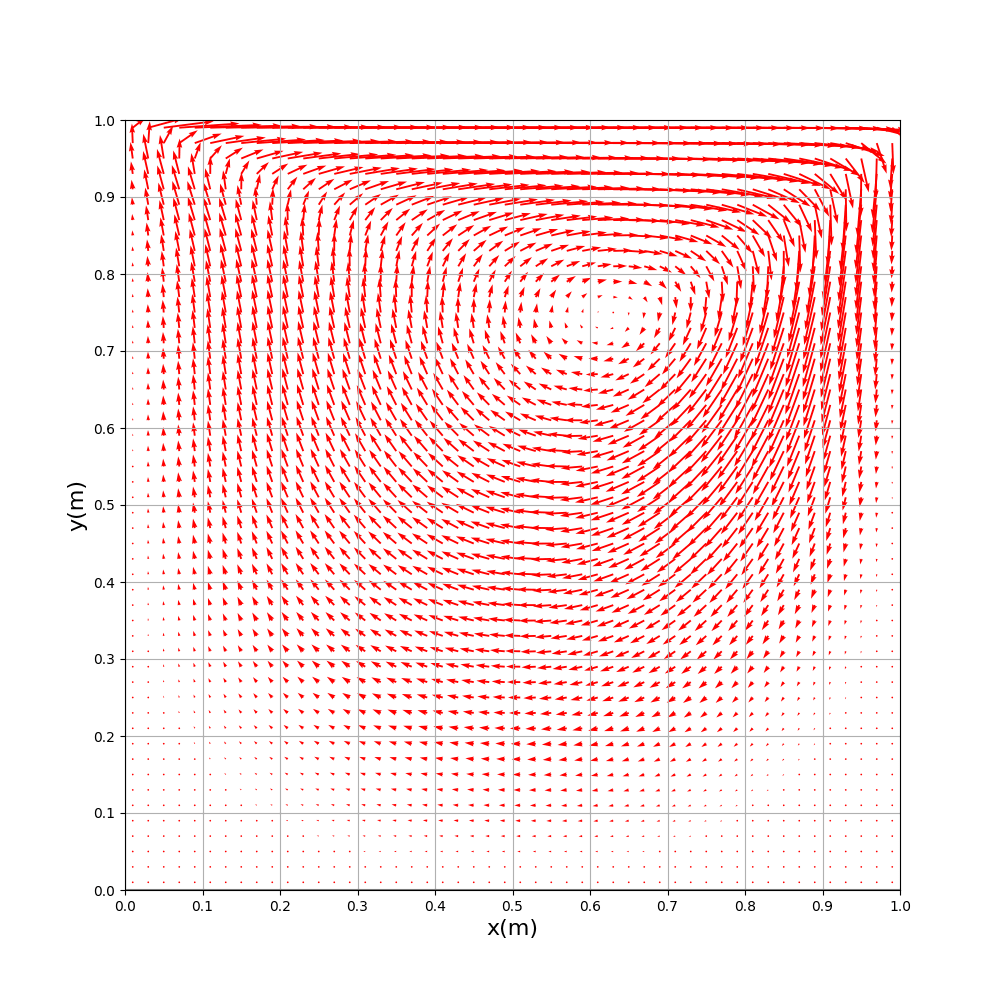
解析から20.0秒後

上部の運動に引きづられて、
流体が動いていることがわかりますね。
また、解析ステップが進むにつれて、
流体の下側部分(Yの値が小さい側)の速度に
変化があることが読み取れます。
解析から5.0秒後と解析から20.0秒後の様相が
殆ど変わりがないことから、
解析から5.0秒後〜20.0秒後の各メッシュの速度変化は殆どないのではと考えられます。
今回レイノルズ数を100に設定しましたが、
レイノルズ数が小⇒粘性力が支配的な層流になり、
レイノルズ数が大⇒慣性力が支配的な乱流と
なりますので、
流れの状態も変わってくるかと想定されます。
今回はシンプルな層流での解析を行ってみました。
Discussion