SIGNATE SOTA アップル 引越し需要予測 備忘録

はじめに

SIGNATE アップル 引越し需要予測SOTAコンペに参加して、48位で決着しました。
様々なアイデアを検証してより良い結果に近づけていく感覚を掴めたので備忘録を書きました。
読者の皆さんの参考になれば幸いです。

リンク

• SIGNATE アップル 引越し需要予測: https://signate.jp/competitions/269

コンペの前に情報収集

SOTAでは先人の知見を序盤から使用できます。
本コンペの記録を残して頂けた方々の記事・ブログを勉強させていただきました。

• 俵 さん、 2020-03-24: https://tawara.hatenablog.com/entry/2020/03/24/084706
• マサ さん、 2020-08-25: https://note.com/masato_ihara/n/nf12ec9bfdf15
• ゆたろ さん、2020-09-22: https://lee-ann-al-chan.com/wp/wp-login.php/2020/09/22/signate_apple_mobing/
• bo-no さん、2020-11-27: https://qiita.com/bo-no/items/2a9cacd9d5a371a23df1
• 60歳からのデータ・サイエンス さん、2021-05-24: https://ameblo.jp/toru59er/entry-12676209989.html
• 株式会社Crosstab 代表取締役 漆畑充 さん、2021-08-31: https://crosstab.co.jp/マーケターのための需要予測-prophetを用いた方法/
• いちろう さん、 2021-11-04: https://sey323log.hatenablog.com/entry/20211104/1636033224
• ヒノマルク さん、2022-08-12: https://www.hinomaruc.com/apple-hikkoshi-analytics-1/
• MAsa_min さん、 2024-03-25: https://qiita.com/MAsa_min/items/d76f7ce005ee6998c39d

下記のメモを取りました。
時系列分析はモデル学習の前にやることが多そうです。

• 金額が欠測値であるレコードを削除する
• 時系列モデリングと木系モデリングのアンサンブル
• datetimeを月、日付カラムに分割する
• 休日フラグ(土日、祝日)
• 六曜番号
• 料金区分の和・積
• LightGBMとProphetモデルの推定値ブレンド
• 去年の同週同曜日の追加
• 特徴量同士の積
• ラグ特徴量、移動平均
• Prophet
• PyCaret(GradientBoostingRegressorとRandomfForestのブレンド)
• リード特徴量(リークでは?)
• AutoGluon
• [データクリーニング] 休業日は引越し数を0にする
• 階差(非定常過程の目的変数を定常過程に変換する)
• AR、MA、ARMA、Auto-ARIMA、SARIMAモデル
• 季節フラグ
• 大型連休フラグ
• 経済指標

EDA

The Kaggle BookのGrand Master、Masterへのインタビューでは度々EDAの重要性が述べられています.
そのコンペが解決したい課題や、そのデータセットの特徴を把握することができれば、解決策を提示できる(モデルを構築できる)とのことです。
これに倣い私もデータの可視化から始めてみます。

リンク

• The Kaggle Book: https://book.impress.co.jp/books/1122101060

import polars as pl# DataFrame
import polars.selectors as cs# polarsのサブモジュール
pl.Config.set_fmt_str_lengths(100)# print, displayの表示制限調整
import numpy as np# 数値計算

import matplotlib.pyplot as plt# グラフ
import japanize_matplotlib# 日本語ラベル
import seaborn as sns# グラフ
%matplotlib inline

from datetime import date# 日時
import matplotlib.dates as mdates# グラフの日時調整

import jpholiday# 休日

from prophet import Prophet# 時系列分析

from sklearn.metrics import mean_absolute_error, make_scorer, r2_score# 評価関数
from sklearn.ensemble import GradientBoostingRegressor# 推定器
from sklearn.model_selection import RepeatedKFold# 交差検証
from sklearn.experimental import enable_halving_search_cv# ハイパーパラメータ最適化
from sklearn.model_selection import HalvingRandomSearchCV# ハイパーパラメータ最適化

データを読み込みます。
この記事では、次のディレクトリ構造を想定しています。

root\
   ┣ data\
   ┃    ┣ input\
   ┃    ┃     ┣ sample_submit.csv
   ┃    ┃     ┣ test.csv
   ┃    ┃     ┗ train.csv
   ┃    ┗ output\
   ┃          ┗ submit.csv
   ┗ notebooks\
        ┗ this_article.ipynb

train = pl.read_csv("../data/input/train.csv")
test = pl.read_csv("../data/input/test.csv")
sample_submit = pl.read_csv("../data/input/sample_submit.csv", has_header = False)

データの概観

データ数を確認します.

print("train:", train.shape, " test:", test.shape, " sample_submit:", sample_submit.shape)

train: (2101, 6)  test: (365, 5)  sample_submit: (364, 2)

ID、目的変数、そして特徴量が4種類のデータセットです。
訓練データセットが2,000個強のため、LightGBMなどの強いライブラリでは過学習に注意する必要があります。
線形回帰の場合は十分なデータがあるでしょう。

先頭5行を表示して、データの概観とデータ型を確認します。

print("train\n", train.head(), "\ntest\n", test.head(), "\nsample_submit\n", sample_submit.head())

train
 shape: (5, 6)
┌────────────┬─────┬────────┬───────┬──────────┬──────────┐
│ datetime   ┆ y   ┆ client ┆ close ┆ price_am ┆ price_pm │
│ ---        ┆ --- ┆ ---    ┆ ---   ┆ ---      ┆ ---      │
│ str        ┆ i64 ┆ i64    ┆ i64   ┆ i64      ┆ i64      │
╞════════════╪═════╪════════╪═══════╪══════════╪══════════╡
│ 2010-07-01 ┆ 17  ┆ 0      ┆ 0     ┆ -1       ┆ -1       │
│ 2010-07-02 ┆ 18  ┆ 0      ┆ 0     ┆ -1       ┆ -1       │
│ 2010-07-03 ┆ 20  ┆ 0      ┆ 0     ┆ -1       ┆ -1       │
│ 2010-07-04 ┆ 20  ┆ 0      ┆ 0     ┆ -1       ┆ -1       │
│ 2010-07-05 ┆ 14  ┆ 0      ┆ 0     ┆ -1       ┆ -1       │
└────────────┴─────┴────────┴───────┴──────────┴──────────┘ 
test
 shape: (5, 5)
┌────────────┬────────┬───────┬──────────┬──────────┐
│ datetime   ┆ client ┆ close ┆ price_am ┆ price_pm │
│ ---        ┆ ---    ┆ ---   ┆ ---      ┆ ---      │
│ str        ┆ i64    ┆ i64   ┆ i64      ┆ i64      │
╞════════════╪════════╪═══════╪══════════╪══════════╡
│ 2016-04-01 ┆ 1      ┆ 0     ┆ 3        ┆ 2        │
│ 2016-04-02 ┆ 0      ┆ 0     ┆ 5        ┆ 5        │
│ 2016-04-03 ┆ 1      ┆ 0     ┆ 2        ┆ 2        │
│ 2016-04-04 ┆ 1      ┆ 0     ┆ 1        ┆ 1        │
│ 2016-04-05 ┆ 0      ┆ 0     ┆ 1        ┆ 1        │
└────────────┴────────┴───────┴──────────┴──────────┘ 
sample_submit
 shape: (5, 2)
┌────────────┬───────────┐
│ column_1   ┆ column_2  │
│ ---        ┆ ---       │
│ str        ┆ f64       │
╞════════════╪═══════════╡
│ 2016-04-01 ┆ 65.989206 │
│ 2016-04-02 ┆ 73.07633  │
│ 2016-04-03 ┆ 62.837857 │
│ 2016-04-04 ┆ 57.607645 │
│ 2016-04-05 ┆ 56.316084 │
└────────────┴───────────┘

IDは日時datetimeカラム、目的変数は引越し数yカラムです。
日時以外のデータは全て整数型です。
データ説明より、clientとcloseが名義尺度、price_amとprice_pmが順序尺度です。
比例尺度どころか間隔尺度も無いため、素朴な線形回帰は難しいかもしれません。

カラム	ヘッダ名称	説明	変数種別
0	datetime	日時（YYYY-MM-DD）	文字列
1	y	引越し数	数値：整数
2	client	法人が絡む特殊な引越し日フラグ	数値：整数（0,1）
3	close	休業日	数値：整数（0,1）
4	price_am	午前の料金区分（-1は欠損を表す。5が最も料金が高い）	数値：整数（-1,0,1,2,3,4,5）
5	price_pm	午後の料金区分（-1は欠損を表す。5が最も料金が高い）	数値：整数（-1,0,1,2,3,4,5）

• 訓練データ: 2010-07-01から2016-03-31までの引越しデータ
• テストデータ: 2016-04-01から2017-03-31までの引越しデータ

リンク

• データ説明: https://signate.jp/competitions/269/data
• 1-4. 変数の尺度: https://bellcurve.jp/statistics/course/1562.html

IDとして使用されているdatetimeカラムを文字列型と日付型に分離します。
カラムの役割を分散することでコードエラーが発生しにくくなります。

train = train.insert_column(0, train["datetime"].alias("id")).with_columns(pl.col("datetime").str.strptime(dtype = pl.Date))
test = test.insert_column(0, test["datetime"].alias("id")).with_columns(pl.col("datetime").str.strptime(dtype = pl.Date))

print(train.head())

目的変数 y (引越し数)

予測したい変数の特徴を把握します。

fig, axes = plt.subplots(
    nrows = 1, ncols = 2, # axの縦・横の数
    height_ratios = [1], width_ratios = [2, 1], # ax の縦・横比
    figsize = (15, 4)
)

# 描画
g_time = sns.lineplot(data = train, x = "datetime", y = "y", ax = axes[0])
g_hist = sns.histplot(data = train, x = "y", ax = axes[1])

# 調整
plt.setp(g_time.get_xticklabels(), rotation = 90)
plt.setp(g_time, ylim = (0, 120))

plt.suptitle("引越し数 y の推移と分布")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

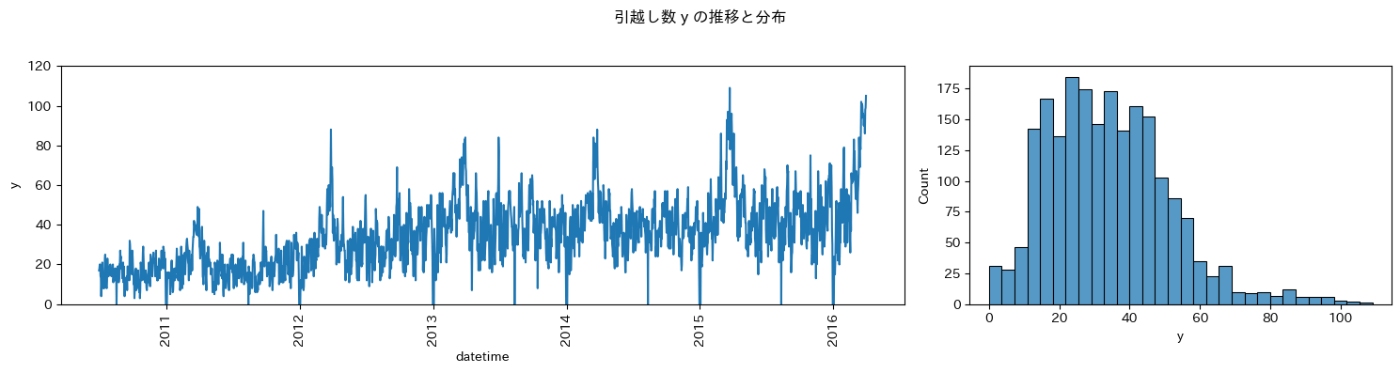
目的変数 y に関して、次のことが分かりました。

• 増加傾向である
• 繫忙期(時系列グラフのピーク)とその他の時期がある
• 0 の日がある
• 分布が非対称である

ひとり言
引越し数が増加傾向であるというビジネスとして喜ばしいことが、このコンペを難しくしています。
何故なら、機械学習モデルは訓練データとテストデータの目的変数の確率分布が等しいことを前提としているので、確率分布が変化すると予測精度が悪化するからです。
例えば、2011年の生データで2012年の引越し数を予測すると、常に小さな予測値が出る人手不足の1年になります。

数式で表すと、施策 $\vec{x}$ 、 日時 $t$ が与えられたときの目的変数 $y$ の分布を推定して利益が最大となる施策 $\vec{x}$ を提案・実行することでビジネスに貢献できるわけですが、毎年の確率分布が異なるため予測精度が上がりません。

$$\int Profit \bigl ( \vec{x}, y \bigr ) \times p \bigl ( y | \vec{x} ; t \bigr ) dy$$

予測精度を高めるために、日時 $t$ の影響をキャンセルする必要があります。

増加傾向

事業成長しているということは目的変数の分布が右にシフトしていくことを意味します。
年と年度のどちらが適切な層別か見てみましょう。

train = (
    train
    .with_columns([
        pl.col("datetime").dt.year().alias("year"),
        pl.when(pl.col("datetime").dt.month() <= 3).then(pl.col("datetime").dt.year() - 1)
        .otherwise(pl.col("datetime").dt.year())
        .alias("fy")
    ])
)

fig, axes = plt.subplots(
    nrows = 2, ncols = 2, # axの縦・横の数
    height_ratios = [1, 1], width_ratios = [2, 1], # ax の縦・横比
    figsize = (15, 8)
)

# 描画
g_time_year = sns.lineplot(data = train, x = "datetime", y = "y", hue = "year", palette = "deep", ax = axes[0, 0])
g_hist_year = sns.histplot(data = train, x = "y", hue = "year", palette = "deep", ax = axes[0, 1])

g_time_fy = sns.lineplot(data = train, x = "datetime", y = "y", hue = "fy", palette = "deep", ax = axes[1, 0])
g_hist_fy = sns.histplot(data = train, x = "y", hue = "fy", palette = "deep", ax = axes[1, 1])


# 調整
plt.setp(g_time_year.get_xticklabels(), rotation = 90)
plt.setp(g_time_year, ylim = (0, 120))
plt.setp(g_time_fy.get_xticklabels(), rotation = 90)
plt.setp(g_time_fy, ylim = (0, 120))

plt.suptitle("年・年度別の引越し数 y の推移と分布")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

繁忙期を一塊で扱える年毎の層別がベターです。

繁忙期

y の分布の右側の裾野が繁忙期です。
コンペ説明より3月、4月が繫忙期とのことですので、繫忙期か否かで層別した分布を表示します。

年間を通して見ると、月別の移動者数（≒引越し者数）は特定の月に大きく偏っています。3月、4月が圧倒的に多く、3月は他の月のおよそ2.5倍、4月はおよそ2倍となっています。引越し会社は、おおよそこの繁忙期に稼ぎ、それ以外をなんとかしのいで年間収支を立てている状況です。これが一因で、繁忙期の引越し料金は高くなります。

リンク

• アップル 引越し需要予測: https://signate.jp/competitions/269

train = train.with_columns(
    (
        (pl.col("datetime").dt.month() == 3)
        | (pl.col("datetime").dt.month() == 4)
    ).alias("is_busy")
)

fig, axes = plt.subplots(
    nrows = 1, ncols = 2, # axの縦・横の数
    height_ratios = [1], width_ratios = [2, 1], # ax の縦・横比
    figsize = (15, 4)
)

# 描画
g_time = sns.lineplot(data = train, x = "datetime", y = "y", hue = "is_busy", palette = "deep", ax = axes[0])
g_hist = sns.histplot(data = train, x = "y", hue = "is_busy", palette = "deep", ax = axes[1])

# 調整
plt.setp(g_time.get_xticklabels(), rotation = 90)
plt.setp(g_time, ylim = (0, 120))

plt.suptitle("引越し数 y の推移と分布")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

繁忙期とその他の時期は分けて考えたほうが良さそうです。
難易度順に次の分け方があります。

1. 別々のモデルで学習・推定させる
2. 繁忙期とその他の時期を分離するクリティカルな特徴量を作成する

y = 0

事業成長をしているにもかかわらず y = 0 の下向きスパイクがあるのは、何か理由があるはずです。
数が多くないので、そのまま表示します。

with pl.Config(tbl_rows = -1):
    print(train.filter(pl.col("y") == 0))

shape: (29, 10)
┌────────────┬────────────┬─────┬────────┬───┬──────────┬──────┬──────┬─────────┐
│ id         ┆ datetime   ┆ y   ┆ client ┆ … ┆ price_pm ┆ year ┆ fy   ┆ is_busy │
│ ---        ┆ ---        ┆ --- ┆ ---    ┆   ┆ ---      ┆ ---  ┆ ---  ┆ ---     │
│ str        ┆ date       ┆ i64 ┆ i64    ┆   ┆ i64      ┆ i32  ┆ i32  ┆ bool    │
╞════════════╪════════════╪═════╪════════╪═══╪══════════╪══════╪══════╪═════════╡
│ 2010-08-18 ┆ 2010-08-18 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2010 ┆ 2010 ┆ false   │
│ 2010-12-31 ┆ 2010-12-31 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2010 ┆ 2010 ┆ false   │
│ 2011-01-01 ┆ 2011-01-01 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2011 ┆ 2010 ┆ false   │
│ 2011-01-02 ┆ 2011-01-02 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2011 ┆ 2010 ┆ false   │
│ 2011-01-03 ┆ 2011-01-03 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2011 ┆ 2010 ┆ false   │
│ 2011-08-14 ┆ 2011-08-14 ┆ 0   ┆ 0      ┆ … ┆ 0        ┆ 2011 ┆ 2011 ┆ false   │
│ 2011-12-31 ┆ 2011-12-31 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2011 ┆ 2011 ┆ false   │
│ 2012-01-01 ┆ 2012-01-01 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2012 ┆ 2011 ┆ false   │
│ 2012-01-02 ┆ 2012-01-02 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2012 ┆ 2011 ┆ false   │
│ 2012-01-03 ┆ 2012-01-03 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2012 ┆ 2011 ┆ false   │
│ 2012-12-31 ┆ 2012-12-31 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2012 ┆ 2012 ┆ false   │
│ 2013-01-01 ┆ 2013-01-01 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2013 ┆ 2012 ┆ false   │
│ 2013-01-02 ┆ 2013-01-02 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2013 ┆ 2012 ┆ false   │
│ 2013-01-03 ┆ 2013-01-03 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2013 ┆ 2012 ┆ false   │
│ 2013-08-12 ┆ 2013-08-12 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2013 ┆ 2013 ┆ false   │
│ 2013-12-31 ┆ 2013-12-31 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2013 ┆ 2013 ┆ false   │
│ 2014-01-01 ┆ 2014-01-01 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2014 ┆ 2013 ┆ false   │
│ 2014-01-02 ┆ 2014-01-02 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2014 ┆ 2013 ┆ false   │
│ 2014-01-03 ┆ 2014-01-03 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2014 ┆ 2013 ┆ false   │
│ 2014-08-12 ┆ 2014-08-12 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2014 ┆ 2014 ┆ false   │
│ 2014-12-31 ┆ 2014-12-31 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2014 ┆ 2014 ┆ false   │
│ 2015-01-01 ┆ 2015-01-01 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2015 ┆ 2014 ┆ false   │
│ 2015-01-02 ┆ 2015-01-02 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2015 ┆ 2014 ┆ false   │
│ 2015-01-03 ┆ 2015-01-03 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2015 ┆ 2014 ┆ false   │
│ 2015-08-12 ┆ 2015-08-12 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2015 ┆ 2015 ┆ false   │
│ 2015-12-31 ┆ 2015-12-31 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2015 ┆ 2015 ┆ false   │
│ 2016-01-01 ┆ 2016-01-01 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2016 ┆ 2015 ┆ false   │
│ 2016-01-02 ┆ 2016-01-02 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2016 ┆ 2015 ┆ false   │
│ 2016-01-03 ┆ 2016-01-03 ┆ 0   ┆ 0      ┆ … ┆ -1       ┆ 2016 ┆ 2015 ┆ false   │
└────────────┴────────────┴─────┴────────┴───┴──────────┴──────┴──────┴─────────┘

お盆と年末年始の休業日(close = 1)のとき、y = 0 です。
例外は2010-08-18と2011-08-14ですが、これもお盆休みだと考えられます。

ルールベースで推定できるデータを分離することで、機械学習モデルがシンプルになります。
(このまま決定木に学習させても、推定値はy = 0 ではなく1か2くらいになります。)

train = train.filter( pl.col("y") != 0 )
test_close = test.filter(pl.col("close") == 1)[["id"]]
test_close = test_close.with_columns(pl.Series("y", [0.0] * len(test_close)))
test = test.filter(pl.col("close") != 1)

print(test_close)

shape: (5, 2)
┌────────────┬─────┐
│ id         ┆ y   │
│ ---        ┆ --- │
│ str        ┆ f64 │
╞════════════╪═════╡
│ 2016-08-16 ┆ 0.0 │
│ 2016-12-31 ┆ 0.0 │
│ 2017-01-01 ┆ 0.0 │
│ 2017-01-02 ┆ 0.0 │
│ 2017-01-03 ┆ 0.0 │
└────────────┴─────┘

分布の非対称性

最も素朴な線形回帰モデルは、測定誤差が正規分布に従うことを仮定しています。
本コンペのような長い裾野があると二乗誤差のペナルティが大きくなって予測性能に悪影響を与えます。
右側の裾野を狭める変数変換を探します。

参考リンク

• パターン認識と機械学習 上 (P29, 線形回帰と正規分布): https://www.maruzen-publishing.co.jp/item/b294524.html
• ボックス=コックス変換: https://bellcurve.jp/statistics/glossary/802.html

train = (
    train
    .with_columns([
        pl.col("y").log().alias("y_ln"),
        ((pl.col("y").pow(1 / 2) - 1) / (1/2)).alias("y_bc_1_2"),
        ((pl.col("y").pow(1 / 10) - 1) / (1/10)).alias("y_bc_1_10"),
    ])
)

fig, axes = plt.subplots(
    nrows = 3, ncols = 2, # axの縦・横の数
    height_ratios = [1, 1, 1], width_ratios = [2, 1], # ax の縦・横比
    figsize = (15, 12)
)

# 描画
g_time_ln = sns.lineplot(data = train, x = "datetime", y = "y_ln", hue = "year", palette = "deep", ax = axes[0, 0])
g_hist_ln = sns.histplot(data = train, x = "y_ln", hue = "year", palette = "deep", ax = axes[0, 1])

g_time_bc_1_2 = sns.lineplot(data = train, x = "datetime", y = "y_bc_1_2", hue = "year", palette = "deep", ax = axes[1, 0])
g_hist_bc_1_2 = sns.histplot(data = train, x = "y_bc_1_2", hue = "year", palette = "deep", ax = axes[1, 1])

g_time_bc_1_10 = sns.lineplot(data = train, x = "datetime", y = "y_bc_1_10", hue = "year", palette = "deep", ax = axes[2, 0])
g_hist_bc_1_10 = sns.histplot(data = train, x = "y_bc_1_10", hue = "year", palette = "deep", ax = axes[2, 1])


# 調整
plt.setp(g_time_ln.get_xticklabels(), rotation = 90)
plt.setp(g_time_ln, ylim = (0, 5), title = "対数変換")
plt.setp(g_time_bc_1_2.get_xticklabels(), rotation = 90)
plt.setp(g_time_bc_1_2, ylim = (0, 20), title = "Box-Cox transformation λ = 1/2")
plt.setp(g_time_bc_1_10.get_xticklabels(), rotation = 90)
plt.setp(g_time_bc_1_10, ylim = (0, 6.5), title = "Box-Cox transformation λ = 1/10")

plt.suptitle("変数変換した y の推移と分布")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

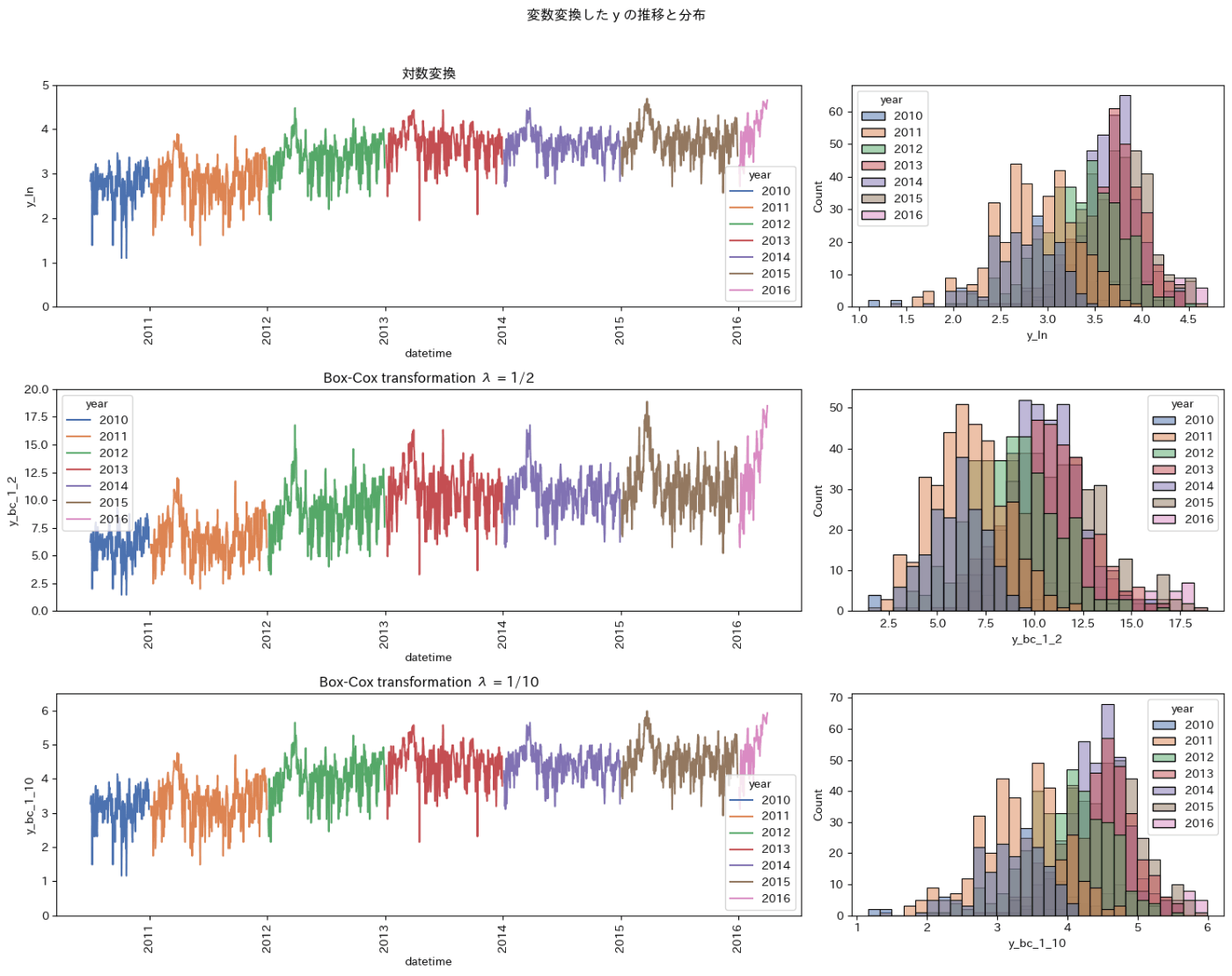
目的変数を対称的な形に近づけて逆変換も簡単な自然対数変換が良いでしょう。

ここまでの前処理を1つのセルにまとめる

複数のセルを跨いだ処理は可読性が悪いので、ここまでの前処理を1つにまとめます。
ただし、年は後で月や日と一緒に追加します。

# データを読み込む
train = pl.read_csv("../data/input/train.csv")
test = pl.read_csv("../data/input/test.csv")
sample_submit = pl.read_csv("../data/input/sample_submit.csv", has_header = False)

# IDと日時を分散する
train = train.insert_column(0, train["datetime"].alias("id")).with_columns(pl.col("datetime").str.strptime(dtype = pl.Date))
test = test.insert_column(0, test["datetime"].alias("id")).with_columns(pl.col("datetime").str.strptime(dtype = pl.Date))

# 休業日(close = 1)を分離する
train = train.filter( pl.col("y") != 0 )
test_close = test.filter(pl.col("close") == 1)[["id"]]
test_close = test_close.with_columns(pl.Series("y", [0.0] * len(test_close)))
test = test.filter(pl.col("close") != 1)

# 目的変数を対数変換する
train = train.insert_column(3, train["y"].log().alias("y_ln"))

print(train.head())

休業日 close

目的変数が0の日、すなわち休業日を分離済みなので、休業日のデータは残っていないはずです。
このことを確認します。

print("訓練データの休業日の数", len(train.filter(pl.col("close") == 1)), "\nテストデータの休業日の数", len(test.filter(pl.col("close") == 1)))

訓練データの休業日の数 0 
テストデータの休業日の数 0

closeカラムのユニーク値が1種類になったので削除します。
節が終わるので、他の前処理とひとまとめにします。

# データを読み込む
train = pl.read_csv("../data/input/train.csv")
test = pl.read_csv("../data/input/test.csv")
sample_submit = pl.read_csv("../data/input/sample_submit.csv", has_header = False)

# IDと日時を分散する
train = train.insert_column(0, train["datetime"].alias("id")).with_columns(pl.col("datetime").str.strptime(dtype = pl.Date))
test = test.insert_column(0, test["datetime"].alias("id")).with_columns(pl.col("datetime").str.strptime(dtype = pl.Date))

# 休業日(close = 1)を分離する
train = train.filter( pl.col("y") != 0 )
test_close = test.filter(pl.col("close") == 1)[["id"]]
test_close = test_close.with_columns(pl.Series("y", [0.0] * len(test_close)))
test = test.filter(pl.col("close") != 1)

# 目的変数を対数変換する
train = train.insert_column(3, train["y"].log().alias("y_ln"))

# ユニーク値が1種類のカラムを削除する
train = train.drop("close")
test = test.drop("close")

print(train.head())

法人が絡む特殊な引越し日フラグ client

特徴量の説明を読んでも良くわからなかったので、とりあえず可視化します。

fig, axes = plt.subplots(
    nrows = 1, ncols = 2, # axの縦・横の数
    height_ratios = [1], width_ratios = [2, 1], # ax の縦・横比
    figsize = (15, 4)
)

# 描画
g_time = sns.lineplot(data = train, x = "datetime", y = "y_ln", hue = "client", ax = axes[0])
g_hist = sns.histplot(data = train, x = "y_ln", hue = "client", ax = axes[1])

# 調整
plt.setp(g_time.get_xticklabels(), rotation = 90)
plt.setp(g_time, ylim = (0, 5))

plt.suptitle("引越し数 y の推移と分布")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

2014年度から法人対応しているようです。
期間を絞ってもう一度可視化します。

fig, axes = plt.subplots(
    nrows = 1, ncols = 2, # axの縦・横の数
    height_ratios = [1], width_ratios = [2, 1], # ax の縦・横比
    figsize = (15, 4)
)

# 描画
g_time = sns.lineplot(data = train.filter(pl.col("datetime") >= date(2014, 5, 1)), x = "datetime", y = "y_ln", hue = "client", palette = "deep", ax = axes[0])
g_hist = sns.histplot(data = train.filter(pl.col("datetime") >= date(2014, 5, 1)), x = "y_ln", hue = "client", palette = "deep", ax = axes[1])

# 調整
plt.setp(g_time.get_xticklabels(), rotation = 90)
plt.setp(g_time, ylim = (0, 5))

plt.suptitle("引越し数 y の推移と分布")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

法人が絡む特殊な引越しを扱う場合、そうでない日に比べて分布が右にシフトするようです。
この特徴量は使えそうです。

平均値も計算しておきます。

print("法人が絡む特殊な引越しを扱う日の引越し数平均", np.round(train.filter(pl.col("datetime") >= date(2014, 5, 1)).filter(pl.col("client") == 1)["y"].mean(), decimals = 2))
print("それ以外の日の引越し数平均", np.round(train.filter(pl.col("datetime") >= date(2014, 5, 1)).filter(pl.col("client") == 0)["y"].mean(), decimals = 2))

法人が絡む特殊な引越しを扱う日の引越し数平均 50.58
それ以外の日の引越し数平均 41.26

料金区分 price_am、price_pm

利益に直結する重要な特徴量です。
まず午前の料金区分と引越し数との関係を可視化します。

fig, axes = plt.subplots(
    nrows = 1, ncols = 2, # axの縦・横の数
    height_ratios = [1], width_ratios = [2, 1], # ax の縦・横比
    figsize = (15, 4)
)

# 描画
g_time = sns.lineplot(data = train, x = "datetime", y = "y_ln", hue = "price_am", palette = "deep", ax = axes[0])
g_hist = sns.histplot(data = train, x = "y_ln", hue = "price_am", palette = "deep", ax = axes[1])

# 調整
plt.setp(g_time.get_xticklabels(), rotation = 90)
plt.setp(g_time, ylim = (0, 5))

plt.suptitle("引越し数 y の推移と分布")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

繁忙期に料金価格を高く設定しているようです(3以上)。
また、2010年の料金価格は全て欠測値です。

同様に午後の料金区分との関係を可視化します。

fig, axes = plt.subplots(
    nrows = 1, ncols = 2, # axの縦・横の数
    height_ratios = [1], width_ratios = [2, 1], # ax の縦・横比
    figsize = (15, 4)
)

# 描画
g_time = sns.lineplot(data = train, x = "datetime", y = "y_ln", hue = "price_pm", palette = "deep", ax = axes[0])
g_hist = sns.histplot(data = train, x = "y_ln", hue = "price_pm", palette = "deep", ax = axes[1])

# 調整
plt.setp(g_time.get_xticklabels(), rotation = 90)
plt.setp(g_time, ylim = (0, 5))

plt.suptitle("引越し数 y の推移と分布")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

午後の猟奇区分も午前と同じ特徴があります。
また、午前よりも料金区分が安い傾向にあります。

fig, axes = plt.subplots(
    nrows = 1, ncols = 2, # axの縦・横の数
    figsize = (10, 4)
)

# 描画
g_hist_am = sns.histplot(data = train, x = "y_ln", hue = "price_am", palette = "deep", ax = axes[0])
g_hist_pm = sns.histplot(data = train, x = "y_ln", hue = "price_pm", palette = "deep", ax = axes[1])

plt.suptitle("引越し数 y の分布")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

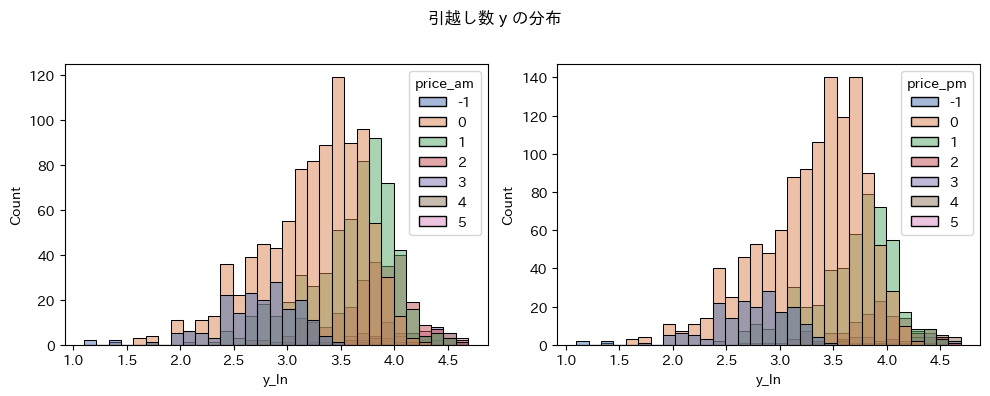
2010年の欠測値

時系列プロットより、2010年の料金区分は全て欠測値です。

print("2010年のデータ数", len(train.filter(pl.col("datetime") <= date(2010, 12, 31))))
print("2010年の午前の料金区分が欠測しているデータ数", len(train.filter((pl.col("datetime") <= date(2010, 12, 31)) & (pl.col("price_am") == -1))))
print("2010年の午後の料金区分が欠測しているデータ数", len(train.filter((pl.col("datetime") <= date(2010, 12, 31)) & (pl.col("price_pm") == -1))))

2010年のデータ数 182
2010年の午前の料金区分が欠測しているデータ数 182
2010年の午後の料金区分が欠測しているデータ数 182

欠測値が182行も連続している場合に欠測値を補完する良い方法はありません。
諦めてデータを削除します。

# データを読み込む
train = pl.read_csv("../data/input/train.csv")
test = pl.read_csv("../data/input/test.csv")
sample_submit = pl.read_csv("../data/input/sample_submit.csv", has_header = False)

# IDと日時を分散する
train = train.insert_column(0, train["datetime"].alias("id")).with_columns(pl.col("datetime").str.strptime(dtype = pl.Date))
test = test.insert_column(0, test["datetime"].alias("id")).with_columns(pl.col("datetime").str.strptime(dtype = pl.Date))

# 休業日(close = 1)を分離する
train = train.filter( pl.col("y") != 0 )
test_close = test.filter(pl.col("close") == 1)[["id"]]
test_close = test_close.with_columns(pl.Series("y", [0.0] * len(test_close)))
test = test.filter(pl.col("close") != 1)

# 目的変数を対数変換する
train = train.insert_column(3, train["y"].log().alias("y_ln"))

# ユニーク値が1種類のカラムを削除する
train = train.drop("close")
test = test.drop("close")

# 2010年の全ての行において料金区分が欠測値のため削除する
train = train.filter(pl.col("datetime") >= date(2011, 1, 1))

print(train.head())

EDAのまとめ

1. 目的変数yが増加傾向のため、年毎の分布が右にシフトしている。
   • to do: 年毎の目的変数yの分布を揃える必要がある。
2. 目的変数yは繁忙期(3月、4月)とそれ以外の時期で分布が異なる
3. 休業日close = 1は目的変数y = 0のため、休業日を分離した。
4. 目的変数y = 0の分布の右側の裾野が広いので対数変換で裾野を狭めた。
5. 法人対応clientを2014年度から始めた
6. 法人が絡む特殊な引越しを行う場合(close = 1)、目的変数の平均値が約9増える
7. 料金区分(price_amとprice_pm)は、繁忙期に高い価格を設定している
8. 2010年の料金区分が全て欠測値のため削除した
9. 午後の料金区分は午前よりも安い傾向にある。

時系列分析

年毎の目的変数yの分布を揃えるために時系列モデルの予測値との差分を計算します。

# 訓練データ
train_pandas = (
    train
    .select([
        "datetime",# 日時
        "y_ln"# 目的変数
    ])
    .rename({
        "datetime": "ds",# 日時のカラム名を ds にする必要がある。
        "y_ln": "y"# 目的変数のカラム名を y にする必要がある。
        })
    .to_pandas()# 機械学習ライブラリとの親和性の高いPnadasに変換する
)
# テストデータ
test_pandas = (
    test
    .select([
        "datetime",# 日時
    ])
    .rename({"datetime": "ds"})# 日時を ds にする必要がある。
    .to_pandas()# 機械学習ライブラリとの親和性の高いPnadasに変換する
)

# モデルの学習
model = Prophet()
model.fit(train_pandas)

# 推定値の算出
forecast_train = pl.Series("y_prophet", model.predict(train_pandas)["yhat"].values)
forecast_test = pl.Series("y_prophet", model.predict(test_pandas)["yhat"].values)

# 推定値をDataFrameに追加する
train = train.insert_column(4, forecast_train)
test = test.insert_column(2, forecast_test)

# 対数変換した目的変数とProphetの予測値の差分を計算する
train = train.insert_column(5, (train["y_ln"] - train["y_prophet"]).alias("y_difference"))

# 確認
print(train.head())
print(test.head())

# 不要なDataFrameを削除する
del train_pandas, test_pandas

年毎に層別した目的変数の自然対数および時系列モデルの予測値の時系列プロットと、これらの差分の分布を可視化します。

train = train.with_columns(pl.col("datetime").dt.year().alias("year"))
test = test.with_columns(pl.col("datetime").dt.year().alias("year"))

fig, axes = plt.subplots(
    nrows = 2, ncols = 2, # axの縦・横の数
    height_ratios = [1, 1], width_ratios = [2, 1], # ax の縦・横比
    figsize = (15, 8)
)

# 描画
g_time_train = sns.lineplot(data = train, x = "datetime", y = "y_ln", hue = "year", palette = "deep", ax = axes[0, 0])
g_time_prophet_train = sns.lineplot(data = train, x = "datetime", y = "y_prophet", ax = axes[0, 0], color = ".1")
g_time_prophet_test = sns.lineplot(data = test, x = "datetime", y = "y_prophet", ax = axes[0, 0], color = ".1")
g_hist_train = sns.histplot(data = train, x = "y_ln", hue = "year", palette = "deep", ax = axes[0, 1])
# 差分
g_residual_train = sns.scatterplot(data = train, x = "datetime", y = "y_difference", hue = "year", palette = "deep", marker = "+", ax = axes[1, 0])
g_residual_hist_train = sns.histplot(data = train, x = "y_difference", hue = "year", palette = "deep", ax = axes[1, 1])

# 調整
plt.setp(g_time_train.get_xticklabels(), rotation = 90)
plt.setp(g_time_train, ylim = (0, 5))
plt.setp(g_residual_train.get_xticklabels(), rotation = 90)
plt.setp(g_residual_train, ylim = (-2.5, 2.5))

plt.suptitle("引越し数 y の推移と、時系列モデルの予測値との差の分布")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

# 不要なカラムの削除
train = train.drop("year")
test = test.drop("year")

自然対数変換した目的変数の予測値との差分を計算することで、年毎の分布を揃えることができました。
テストデータ(2016-04-01 ~ 2017-03-31)と訓練データ(2011-01-01 ~ 2016-03-31)の目的変数の確率分布が等しいとみなせるようになりました。
LightGBM等の強力なライブラリの予測精度が安定します。
また、交差検証に関しても、TimeSeriesだけでなく無作為抽出も使用できるかもしれません。

$$p \bigl ( y | \vec{x} ; t \bigr ) \ \rightarrow \ p \bigl ( \delta y | \vec{x} \bigr )$$

機械学習モデルによる学習 01

最初のモデルは、与えられた特徴量のみを使用するシンプルなモデルです。

訓練データ、検証データを分割する

モデル性能を検証するために、訓練データを学習用と評価用に分割します。
train_test_split関数が良く使われますが、今回はNumpyのマスクを使用します。

# 機械学習ライブラリと親和性の高いPandasに変換する
train_pandas = train.to_pandas().set_index("id")

# 目的変数と特徴量
target_column = "y_difference"
feature_columns = ["client", "price_am", "price_pm"]

# 訓練データと評価データに分割するマスク
np.random.seed(1192)
train_mask_1 = np.random.choice([True, False], size = len(train_pandas), p = [0.75, 0.25])

# 説明変数、目的変数の分割
train_temp, valid_temp = train_pandas[train_mask_1], train_pandas[~train_mask_1]
X_train, y_train = train_temp[feature_columns], train_temp[target_column]
X_valid, y_valid = valid_temp[feature_columns], valid_temp[target_column]

デフォルトのハイパーパラメータで学習する

# 学習
est = GradientBoostingRegressor(random_state = 1192).fit(X_train, y_train)

# 予測(対数変換を逆変換する)
y_pred_train = np.exp(est.predict(X_train) + train_temp["y_prophet"])
y_pred_valid = np.exp(est.predict(X_valid) + valid_temp["y_prophet"])


# 予測精度の確認
print("訓練データの評価関数:", np.round(mean_absolute_error(train_temp["y"], y_pred_train), decimals = 7))# 小数第7位はコンペスコアの有効数字
print("評価データの評価関数:", np.round(mean_absolute_error(valid_temp["y"], y_pred_valid), decimals = 7))

# 予測結果の確認
fig, axes = plt.subplots(
    nrows = 2, ncols = 2, # axの縦・横の数
    height_ratios = [1, 1], width_ratios = [2, 1], # ax の縦・横比
    figsize = (15, 8)
)

# 描画
g_time_train = sns.lineplot(data = train, x = "datetime", y = "y", ax = axes[0, 0])
g_predict_train = sns.lineplot(x = train_temp["datetime"], y = y_pred_train, ax = axes[0, 0])
g_predict_valid = sns.lineplot(x = valid_temp["datetime"], y = y_pred_valid, ax = axes[0, 0])

g_hist_train = sns.histplot(data = train, x = "y", ax = axes[0, 1])
g_predict_hist_train = sns.histplot(x = y_pred_train, ax = axes[0, 1])
g_predict_hist_valid = sns.histplot(x = y_pred_valid, ax = axes[0, 1])

# 残差
g_residual_dummy = sns.scatterplot(x = [date(2011, 1, 1)], y = 0, marker = "+", ax = axes[1, 0])
g_residual_train = sns.scatterplot(x = train_temp["datetime"], y = y_pred_train - train_temp["y"], marker = "+", ax = axes[1, 0])
g_residual_valid = sns.scatterplot(x = valid_temp["datetime"], y = y_pred_valid - valid_temp["y"], marker = "+", ax = axes[1, 0])

g_residual_hist_dummy = sns.histplot(x = [0], ax = axes[1, 1])
g_residual_hist_train = sns.histplot(x = y_pred_train - train_temp["y"], ax = axes[1, 1])
g_residual_hist_valid = sns.histplot(x = y_pred_valid - valid_temp["y"], ax = axes[1, 1])


# 調整
plt.setp(g_time_train.get_xticklabels(), rotation = 90)
plt.setp(g_time_train, ylim = (0, 120))

plt.suptitle("引越し数 y の予測精度の確認")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

# 特徴量の重要度
df_feature_importance = pl.DataFrame({
    "feature": est.feature_names_in_,
    "importance": est.feature_importances_
})
g_importance = sns.barplot(data = df_feature_importance, x = "importance", y = "feature")
plt.setp(g_importance, title = "特徴量の重要度")

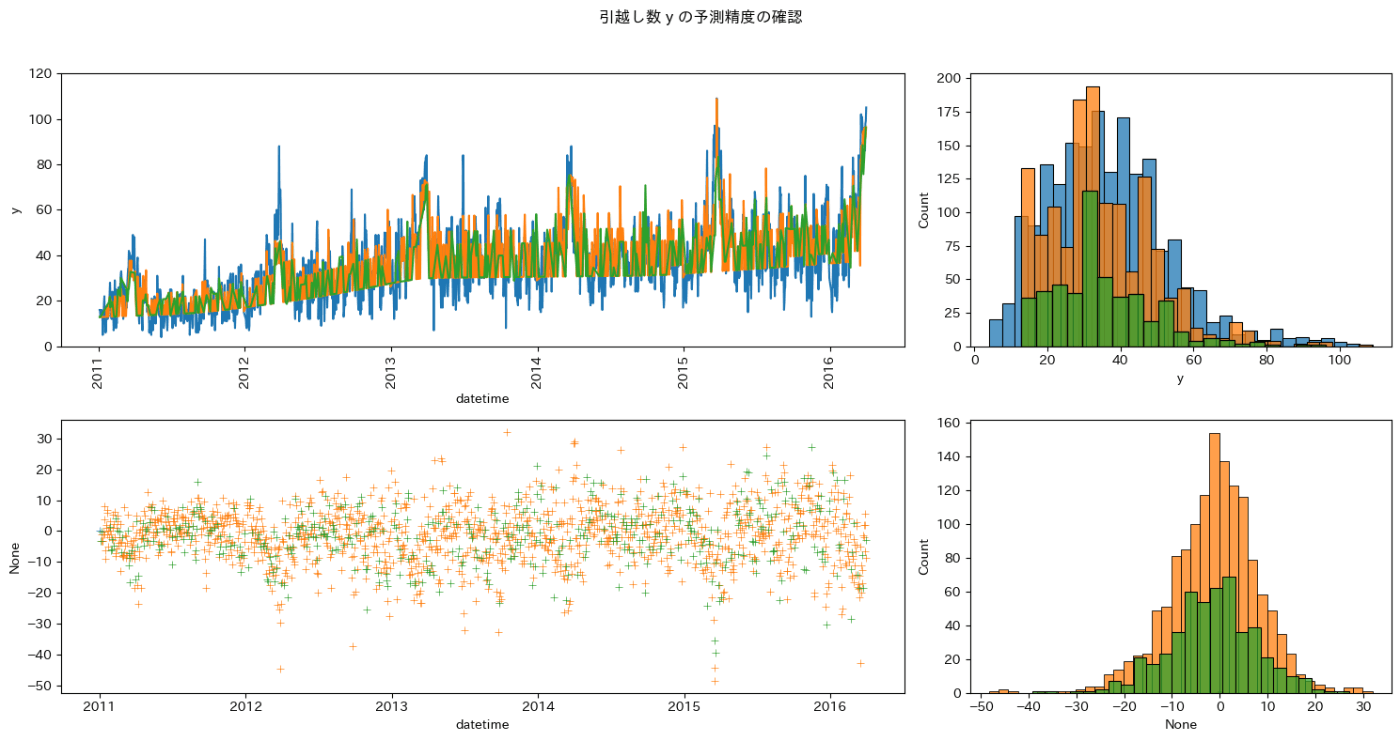
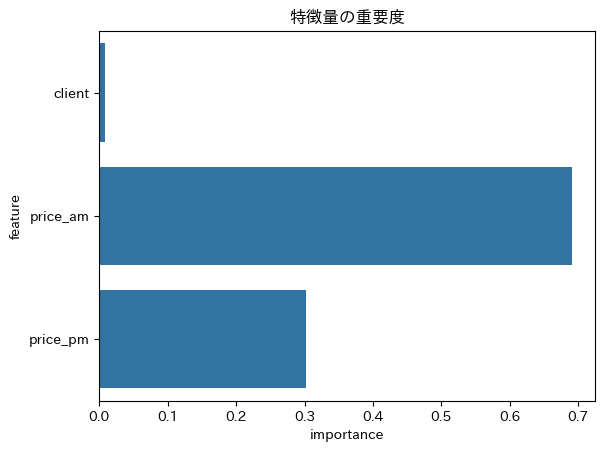
引越し数が少ない日の予測に課題があります。
しかし、訓練データと検証データの残差の分布がほぼ同じであるため、このモデルは安定して予測ができそうです。
予測精度を上げるための工夫を加えていきます。

繁忙期とその他の時期でモデルを分ける

データを分割して別のモデルに学習させることで精度が上がることがあります。
3、4月が繁忙期なので、繁忙期とそれ以外で学習させてみます。

年間を通して見ると、月別の移動者数（≒引越し者数）は特定の月に大きく偏っています。3月、4月が圧倒的に多く、3月は他の月のおよそ2.5倍、4月はおよそ2倍となっています。引越し会社は、おおよそこの繁忙期に稼ぎ、それ以外をなんとかしのいで年間収支を立てている状況です。これが一因で、繁忙期の引越し料金は高くなります。

リンク:

• アップル 引越し需要予測 | SIGNATE - Data Science Competition: https://signate.jp/competitions/269

# Pandasに変換
train_busy_pandas = train.filter( (pl.col("datetime").dt.month() == 3) | (pl.col("datetime").dt.month() == 4) ).to_pandas().set_index("id")
train_other_pandas = train.filter( ~((pl.col("datetime").dt.month() == 3) | (pl.col("datetime").dt.month() == 4)) ).to_pandas().set_index("id")

# 目的変数と特徴量
target_column = "y_difference"
feature_columns = ["client", "price_am", "price_pm"]

# 訓練データと評価データに分割するマスク
np.random.seed(1192)
train_mask_busy_1 = np.random.choice([True, False], size = len(train_busy_pandas), p = [0.75, 0.25])
train_mask_other_1 = np.random.choice([True, False], size = len(train_other_pandas), p = [0.75, 0.25])


# 説明変数、目的変数の分割
train_busy_temp, valid_busy_temp = train_busy_pandas[train_mask_busy_1], train_busy_pandas[~train_mask_busy_1]
X_train_busy, y_train_busy = train_busy_temp[feature_columns], train_busy_temp[target_column]
X_valid_busy, y_valid_busy = valid_busy_temp[feature_columns], valid_busy_temp[target_column]

train_other_temp, valid_other_temp = train_other_pandas[train_mask_other_1], train_other_pandas[~train_mask_other_1]
X_train_other, y_train_other = train_other_temp[feature_columns], train_other_temp[target_column]
X_valid_other, y_valid_other = valid_other_temp[feature_columns], valid_other_temp[target_column]

# 学習
est_busy = GradientBoostingRegressor(random_state = 1192).fit(X_train_busy, y_train_busy)
est_other = GradientBoostingRegressor(random_state = 1192).fit(X_train_other, y_train_other)


# 予測(対数変換を逆変換する)
y_pred_train_busy = np.exp(est.predict(X_train_busy) + train_busy_temp["y_prophet"])
y_pred_valid_busy = np.exp(est.predict(X_valid_busy) + valid_busy_temp["y_prophet"])

y_pred_train_other = np.exp(est.predict(X_train_other) + train_other_temp["y_prophet"])
y_pred_valid_other = np.exp(est.predict(X_valid_other) + valid_other_temp["y_prophet"])


# 予測精度の確認
# 小数第7位はコンペスコアの有効数字
print("繁忙期の訓練データの評価関数:", np.round(mean_absolute_error(train_busy_temp["y"], y_pred_train_busy), decimals = 7))
print("繁忙期の評価データの評価関数:", np.round(mean_absolute_error(valid_busy_temp["y"], y_pred_valid_busy), decimals = 7))
print("その他の時期の訓練データの評価関数:", np.round(mean_absolute_error(train_other_temp["y"], y_pred_train_other), decimals = 7))
print("その他の時期の評価データの評価関数:", np.round(mean_absolute_error(valid_other_temp["y"], y_pred_valid_other), decimals = 7))



# 予測結果の確認
fig, axes = plt.subplots(
    nrows = 2, ncols = 2, # axの縦・横の数
    height_ratios = [1, 1], width_ratios = [2, 1], # ax の縦・横比
    figsize = (15, 8)
)

# 描画
g_time_train = sns.lineplot(data = train, x = "datetime", y = "y", ax = axes[0, 0])
#g_predict_train_busy = sns.lineplot(x = train_busy_temp["datetime"], y = y_pred_train_busy, ax = axes[0, 0])
g_predict_valid_busy = sns.lineplot(x = valid_busy_temp["datetime"], y = y_pred_valid_busy, ax = axes[0, 0])

#g_predict_train_other = sns.lineplot(x = train_other_temp["datetime"], y = y_pred_train_other, ax = axes[0, 0])
g_predict_valid_other = sns.lineplot(x = valid_other_temp["datetime"], y = y_pred_valid_other, ax = axes[0, 0])


g_hist_train = sns.histplot(data = train, x = "y", ax = axes[0, 1])
#g_predict_hist_train_busy = sns.histplot(x = y_pred_train_busy, ax = axes[0, 1])
g_predict_hist_valid_busy = sns.histplot(x = y_pred_valid_busy, ax = axes[0, 1])
#g_predict_hist_train_other = sns.histplot(x = y_pred_train_other, ax = axes[0, 1])
g_predict_hist_valid_other = sns.histplot(x = y_pred_valid_other, ax = axes[0, 1])


# 残差
g_residual_dummy = sns.scatterplot(x = [date(2011, 1, 1)], y = 0, marker = "+", ax = axes[1, 0])
#g_residual_train_busy = sns.scatterplot(x = train_busy_temp["datetime"], y = y_pred_train_busy - train_busy_temp["y"], marker = "+", ax = axes[1, 0])
g_residual_valid_busy = sns.scatterplot(x = valid_busy_temp["datetime"], y = y_pred_valid_busy - valid_busy_temp["y"], marker = "+", ax = axes[1, 0])
#g_residual_train_other = sns.scatterplot(x = train_other_temp["datetime"], y = y_pred_train_other - train_other_temp["y"], marker = "+", ax = axes[1, 0])
g_residual_valid_other = sns.scatterplot(x = valid_other_temp["datetime"], y = y_pred_valid_other - valid_other_temp["y"], marker = "+", ax = axes[1, 0])

g_residual_hist_dummy = sns.histplot(x = [0], ax = axes[1, 1])
#g_residual_hist_train_busy = sns.histplot(x = y_pred_train_busy - train_busy_temp["y"], ax = axes[1, 1])
g_residual_hist_valid_busy = sns.histplot(x = y_pred_valid_busy - valid_busy_temp["y"], ax = axes[1, 1])
#g_residual_hist_train_other = sns.histplot(x = y_pred_train_other - train_other_temp["y"], ax = axes[1, 1])
g_residual_hist_valid_other = sns.histplot(x = y_pred_valid_other - valid_other_temp["y"], ax = axes[1, 1])

# 調整
plt.setp(g_time_train.get_xticklabels(), rotation = 90)
plt.setp(g_time_train, ylim = (0, 120))

plt.suptitle("引越し数 y の予測精度の確認")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

# 特徴量の重要度
df_feature_importance = pl.DataFrame({
    "feature": est.feature_names_in_,
    "importance": est.feature_importances_
})
g_importance = sns.barplot(data = df_feature_importance, x = "importance", y = "feature")
plt.setp(g_importance, title = "特徴量の重要度")

忙期の訓練データの評価関数: 9.5800508
繁忙期の評価データの評価関数: 10.0742794
その他の時期の訓練データの評価関数: 6.6299591
その他の時期の評価データの評価関数: 6.2124975

繁忙期の予測精度が悪化しました。
特徴量が3つしかない状況では時期尚早ということだったのでしょう。
特徴量を追加してから再挑戦します。

特徴量を追加して学習する

これまでの前処理を1つのセルにまとめた後に、事前調査を含めて思いつく限りの特徴量を追加しましょう。

# データを読み込む
train = pl.read_csv("../data/input/train.csv")
test = pl.read_csv("../data/input/test.csv")
sample_submit = pl.read_csv("../data/input/sample_submit.csv", has_header = False)

# IDと日時を分散する
train = train.insert_column(0, train["datetime"].alias("id")).with_columns(pl.col("datetime").str.strptime(dtype = pl.Date))
test = test.insert_column(0, test["datetime"].alias("id")).with_columns(pl.col("datetime").str.strptime(dtype = pl.Date))

# 休業日(close = 1)を分離する
train = train.filter( pl.col("y") != 0 )
test_close = test.filter(pl.col("close") == 1)[["id"]]
test_close = test_close.with_columns(pl.Series("y", [0.0] * len(test_close)))
test = test.filter(pl.col("close") != 1)

# 目的変数を対数変換する
train = train.insert_column(3, train["y"].log().alias("y_ln"))

# ユニーク値が1種類のカラムを削除する
train = train.drop("close")
test = test.drop("close")

# 2010年の全ての行において料金区分が欠測値のため削除する
train = train.filter(pl.col("datetime") >= date(2011, 1, 1))

# Prophetの推定値と差分を追加する
train = train.insert_column(4, forecast_train)
test = test.insert_column(2, forecast_test)
train = train.insert_column(5, (train["y_ln"] - train["y_prophet"]).alias("y_difference"))

print(train.head())

train = (
    train
    # 日付の基本要素の追加
    .with_columns([
        # 年
        pl.col("datetime").dt.year().alias("year"),
        # 四半期・月・週・日(年の分割)
        pl.col("datetime").dt.quarter().alias("quarter"),
        pl.col("datetime").dt.month().alias("month"),
        pl.col("datetime").dt.week().alias("week"),
        pl.col("datetime").dt.ordinal_day().alias("ordinal_day"),
        # 週目・日・月末までの日数(月の分割)
        (pl.col("datetime").dt.day() // 7 + 1).alias("week_of_month"),
        pl.col("datetime").dt.day().alias("day"),
        # 曜日(週の分割)
        pl.col("datetime").dt.weekday().alias("day_of_week"),
    ])
    # 四半期はじめ, 月初めのフラグ
    .with_columns([
        pl.when((pl.col("month").is_in([1, 4, 7, 10])) & (pl.col("day") == 1)).then(1)
        .otherwise(0).alias("quarter_start"),
        pl.when((pl.col("month").is_in([3, 6, 9, 12])) & (pl.col("datetime") == pl.col("datetime").dt.month_end())).then(1)
        .otherwise(0).alias("quarter_end"),
        pl.when(pl.col("day") == 1).then(1)
        .otherwise(0).alias("month_start"),
        pl.when(pl.col("datetime") == pl.col("datetime").dt.month_end()).then(1)
        .otherwise(0).alias("month_end"),    
    ])
    # 価格の和・差・積
    .with_columns([
        (pl.col("price_am") + pl.col("price_pm")).alias("price_sum"),
        (pl.col("price_am") - pl.col("price_pm")).alias("price_difference"),
        ((pl.col("price_am") + 1) * (pl.col("price_pm") + 1)).alias("price_product"),
    ])
)

test = (
    test
    # 日付の基本要素の追加
    .with_columns([
        # 年
        pl.col("datetime").dt.year().alias("year"),
        # 四半期・月・週・日(年の分割)
        pl.col("datetime").dt.quarter().alias("quarter"),
        pl.col("datetime").dt.month().alias("month"),
        pl.col("datetime").dt.week().alias("week"),
        pl.col("datetime").dt.ordinal_day().alias("ordinal_day"),
        # 週目・日・月末までの日数(月の分割)
        (pl.col("datetime").dt.day() // 7 + 1).alias("week_of_month"),
        pl.col("datetime").dt.day().alias("day"),
        # 曜日(週の分割)
        pl.col("datetime").dt.weekday().alias("day_of_week"),
    ])
    # 四半期はじめ, 月初めのフラグ
    .with_columns([
        pl.when((pl.col("month").is_in([1, 4, 7, 10])) & (pl.col("day") == 1)).then(1)
        .otherwise(0).alias("quarter_start"),
        pl.when((pl.col("month").is_in([3, 6, 9, 12])) & (pl.col("datetime") == pl.col("datetime").dt.month_end())).then(1)
        .otherwise(0).alias("quarter_end"),
        pl.when(pl.col("day") == 1).then(1)
        .otherwise(0).alias("month_start"),
        pl.when(pl.col("datetime") == pl.col("datetime").dt.month_end()).then(1)
        .otherwise(0).alias("month_end"),    
    ])
    # 価格の和・差・積
    .with_columns([
        (pl.col("price_am") + pl.col("price_pm")).alias("price_sum"),
        (pl.col("price_am") - pl.col("price_pm")).alias("price_difference"),
        ((pl.col("price_am") + 1) * (pl.col("price_pm") + 1)).alias("price_product"),
    ])
)

# 祝日
holiday_list = []
for pair in jpholiday.between(date(2010, 1, 1), date(2017, 12, 31)):
    #print(pair[0], ":\t", pair[1])
    holiday_list.append(pair[0])


# GW
# https://9rando.info/j-holiday/gw/2011/
gw_list = [
    date(2011, 4, 29), date(2011, 4, 30), date(2011, 5, 1),
    date(2011, 5, 2),# 有給休暇の可能性
    date(2011, 5, 3), date(2011, 5, 4), date(2011, 5, 5),

    date(2012, 4, 28), date(2012, 4, 29), date(2012, 4, 30), date(2012, 5, 1),
    date(2012, 5, 2),# 有休
    date(2012, 5, 3), date(2012, 5, 4), date(2012, 5, 5), date(2012, 5, 5),

    date(2013, 4, 27), date(2013, 4, 28), date(2013, 4, 29),
    date(2013, 4, 30), date(2013, 5, 1), date(2013, 5, 2),# 有休
    date(2013, 5, 3), date(2013, 5, 4), date(2013, 5, 5), date(2013, 5, 5), date(2013, 5, 6),

    date(2014, 4, 29),
    date(2014, 4, 30), date(2014, 5, 1), date(2014, 5, 2),# 有休
    date(2014, 5, 3), date(2014, 5, 4), date(2014, 5, 5), date(2014, 5, 5), date(2014, 5, 6),

    date(2015, 4, 29),
    date(2015, 4, 30), date(2015, 5, 1),# 有休
    date(2015, 5, 2), date(2015, 5, 3), date(2015, 5, 4), date(2015, 5, 5), date(2015, 5, 5), date(2015, 5, 6),

    date(2016, 4, 29), date(2016, 4, 30), date(2016, 5, 1),
    date(2016, 5, 2),# 有休
    date(2016, 5, 3), date(2016, 5, 4), date(2016, 5, 5),

    date(2017, 4, 29), date(2017, 4, 30),
    date(2017, 5, 1), date(2017, 5, 2),# 有休
    date(2017, 5, 3), date(2017, 5, 4), date(2017, 5, 5), date(2017, 5, 6), date(2017, 5, 7),
]


# お盆
# https://9rando.info/j-holiday/obon/2011/
obon_list = [
    date(2011, 8, 13), date(2011, 8, 14), date(2011, 8, 15), date(2011, 8, 16),
    date(2012, 8, 13), date(2012, 8, 14), date(2012, 8, 15), date(2012, 8, 16),
    date(2013, 8, 13), date(2013, 8, 14), date(2013, 8, 15), date(2013, 8, 16),
    date(2014, 8, 13), date(2014, 8, 14), date(2014, 8, 15), date(2014, 8, 16),
    date(2015, 8, 13), date(2015, 8, 14), date(2015, 8, 15), date(2015, 8, 16),
    date(2016, 8, 13), date(2016, 8, 14), date(2016, 8, 15), date(2016, 8, 16),
    date(2017, 8, 13), date(2017, 8, 14), date(2017, 8, 15), date(2017, 8, 16),
]


# SW
# https://9rando.info/j-holiday/sw/2011/
sw_list = [
    date(2011, 9, 17), date(2011, 9, 18), date(2011, 9, 19),
    date(2011, 9, 20), date(2011, 9, 21), date(2011, 9, 22),# 有休
    date(2011, 9, 23), date(2011, 9, 24), date(2011, 9, 25),

    date(2012, 9, 15), date(2012, 9, 16), date(2012, 9, 17),
    date(2012, 9, 18), date(2012, 9, 19), date(2012, 9, 20), date(2012, 9, 21),# 有休
    date(2012, 9, 22), date(2012, 9, 23), date(2012, 9, 24),

    date(2013, 9, 14),date(2013, 9, 15), date(2013, 9, 16),
    date(2013, 9, 17), date(2013, 9, 18), date(2013, 9, 19), date(2013, 9, 20),# 有休
    date(2013, 9, 21),date(2013, 9, 22), date(2013, 9, 23),

    date(2014, 9, 13), date(2014, 9, 14),date(2014, 9, 15),
    date(2014, 9, 16), date(2014, 9, 17), date(2014, 9, 18), date(2014, 9, 19),# 有休
    date(2014, 9, 20), date(2014, 9, 21),date(2014, 9, 22),

    date(2015, 9, 19), date(2015, 9, 20), date(2015, 9, 21),
    date(2015, 9, 22), date(2015, 9, 23),

    date(2016, 9, 17), date(2016, 9, 18), date(2016, 9, 19),
    date(2016, 9, 20), date(2016, 9, 21),# 有休
    date(2016, 9, 22),

    date(2017, 9, 16), date(2017, 9, 17), date(2017, 9, 18),
    date(2017, 9, 19), date(2017, 9, 20), date(2017, 9, 21), date(2017, 9, 22),# 有休
    date(2017, 9, 23), date(2017, 9, 24),
]


# 休日フラグを追加する
train = train.with_columns([
    # 祝日
    pl.when(pl.col("datetime").is_in(holiday_list)).then(1)
    .otherwise(0).alias("holiday"),
    # GW
    pl.when(pl.col("datetime").is_in(gw_list)).then(1)
    .otherwise(0).alias("gw"),
    # 盆
    pl.when(pl.col("datetime").is_in(obon_list)).then(1)
    .otherwise(0).alias("obon"),
    # SW
    pl.when(pl.col("datetime").is_in(sw_list)).then(1)
    .otherwise(0).alias("sw"),
    # 土日
    pl.when( pl.col("day_of_week") >= 6 ).then(1)
    .otherwise(0).alias("sat_sun"),
])

test = test.with_columns([
    # 祝日
    pl.when(pl.col("datetime").is_in(holiday_list)).then(1)
    .otherwise(0).alias("holiday"),
    # GW
    pl.when(pl.col("datetime").is_in(gw_list)).then(1)
    .otherwise(0).alias("gw"),
    # 盆
    pl.when(pl.col("datetime").is_in(obon_list)).then(1)
    .otherwise(0).alias("obon"),
    # SW
    pl.when(pl.col("datetime").is_in(sw_list)).then(1)
    .otherwise(0).alias("sw"),
    # 土日
    pl.when( pl.col("day_of_week") >= 6 ).then(1)
    .otherwise(0).alias("sat_sun"),
])

# 不要なリストを削除する
del holiday_list, gw_list, obon_list, sw_list

シンプルなモデルで学習する

特徴量を追加した効果を検証します。

# 機械学習ライブラリと親和性の高いPandasに変換する
train_pandas = train.to_pandas().set_index("id")

# 目的変数と特徴量
target_column = "y_difference"
feature_columns = ['client', 'price_am', 'price_pm',
                    'year', 'quarter', 'month', 'week', 'ordinal_day', 'week_of_month', 'day', 'day_of_week',
                    'quarter_start', 'quarter_end', 'month_start', 'month_end',
                    'price_sum', 'price_difference', 'price_product',
                    'holiday', 'gw', 'obon', 'sw', 'sat_sun'
 ]

# 訓練データと評価データに分割するマスク
np.random.seed(1192)
train_mask_1 = np.random.choice([True, False], size = len(train_pandas), p = [0.75, 0.25])

# 説明変数、目的変数の分割
train_temp, valid_temp = train_pandas[train_mask_1], train_pandas[~train_mask_1]
X_train, y_train = train_temp[feature_columns], train_temp[target_column]
X_valid, y_valid = valid_temp[feature_columns], valid_temp[target_column]

# 学習
est = GradientBoostingRegressor(random_state = 1192).fit(X_train, y_train)

# 予測(対数変換を逆変換する)
y_pred_train = np.exp(est.predict(X_train) + train_temp["y_prophet"])
y_pred_valid = np.exp(est.predict(X_valid) + valid_temp["y_prophet"])


# 予測精度の確認
print("訓練データの評価関数:", np.round(mean_absolute_error(train_temp["y"], y_pred_train), decimals = 7))# 小数第7位はコンペスコアの有効数字
print("評価データの評価関数:", np.round(mean_absolute_error(valid_temp["y"], y_pred_valid), decimals = 7))

# 予測結果の確認
fig, axes = plt.subplots(
    nrows = 2, ncols = 2, # axの縦・横の数
    height_ratios = [1, 1], width_ratios = [2, 1], # ax の縦・横比
    figsize = (15, 8)
)

# 描画
g_time_train = sns.lineplot(data = train, x = "datetime", y = "y", ax = axes[0, 0])
g_predict_train = sns.lineplot(x = train_temp["datetime"], y = y_pred_train, ax = axes[0, 0])
g_predict_valid = sns.lineplot(x = valid_temp["datetime"], y = y_pred_valid, ax = axes[0, 0])

g_hist_train = sns.histplot(data = train, x = "y", ax = axes[0, 1])
g_predict_hist_train = sns.histplot(x = y_pred_train, ax = axes[0, 1])
g_predict_hist_valid = sns.histplot(x = y_pred_valid, ax = axes[0, 1])

# 残差
g_residual_dummy = sns.scatterplot(x = [date(2011, 1, 1)], y = 0, marker = "+", ax = axes[1, 0])
g_residual_train = sns.scatterplot(x = train_temp["datetime"], y = y_pred_train - train_temp["y"], marker = "+", ax = axes[1, 0])
g_residual_valid = sns.scatterplot(x = valid_temp["datetime"], y = y_pred_valid - valid_temp["y"], marker = "+", ax = axes[1, 0])

g_residual_hist_dummy = sns.histplot(x = [0], ax = axes[1, 1])
g_residual_hist_train = sns.histplot(x = y_pred_train - train_temp["y"], ax = axes[1, 1])
g_residual_hist_valid = sns.histplot(x = y_pred_valid - valid_temp["y"], ax = axes[1, 1])


# 調整
plt.setp(g_time_train.get_xticklabels(), rotation = 90)
plt.setp(g_time_train, ylim = (0, 120))

plt.suptitle("引越し数 y の予測精度の確認")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

# 特徴量の重要度
df_feature_importance = pl.DataFrame({
    "feature": est.feature_names_in_,
    "importance": est.feature_importances_
})
g_importance = sns.barplot(data = df_feature_importance, x = "importance", y = "feature")
plt.setp(g_importance, title = "特徴量の重要度")

訓練データの評価関数: 4.7227557
評価データの評価関数: 5.2050808

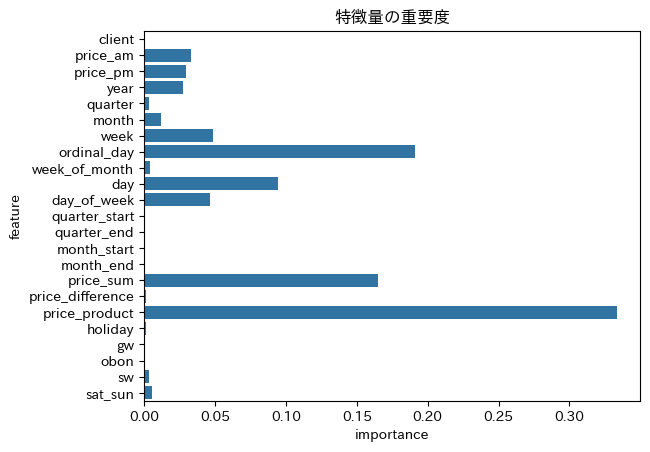
特徴量を追加することで予測精度が改善しました。
もう一度繫忙期とそれ以外の時期に分けて学習させてみます。

繫忙期とそれ以外の時期

# Pandasに変換
train_busy_pandas = train.filter( (pl.col("datetime").dt.month() == 3) | (pl.col("datetime").dt.month() == 4) ).to_pandas().set_index("id")
train_other_pandas = train.filter( ~((pl.col("datetime").dt.month() == 3) | (pl.col("datetime").dt.month() == 4)) ).to_pandas().set_index("id")

# 目的変数と特徴量
target_column = "y_difference"
feature_columns = ['client', 'price_am', 'price_pm',
                    'year', 'quarter', 'month', 'week', 'ordinal_day', 'week_of_month', 'day', 'day_of_week',
                    'quarter_start', 'quarter_end', 'month_start', 'month_end',
                    'price_sum', 'price_difference', 'price_product',
                    'holiday', 'gw', 'obon', 'sw', 'sat_sun'
 ]

# 訓練データと評価データに分割するマスク
np.random.seed(1192)
train_mask_busy_1 = np.random.choice([True, False], size = len(train_busy_pandas), p = [0.75, 0.25])
train_mask_other_1 = np.random.choice([True, False], size = len(train_other_pandas), p = [0.75, 0.25])


# 説明変数、目的変数の分割
train_busy_temp, valid_busy_temp = train_busy_pandas[train_mask_busy_1], train_busy_pandas[~train_mask_busy_1]
X_train_busy, y_train_busy = train_busy_temp[feature_columns], train_busy_temp[target_column]
X_valid_busy, y_valid_busy = valid_busy_temp[feature_columns], valid_busy_temp[target_column]

train_other_temp, valid_other_temp = train_other_pandas[train_mask_other_1], train_other_pandas[~train_mask_other_1]
X_train_other, y_train_other = train_other_temp[feature_columns], train_other_temp[target_column]
X_valid_other, y_valid_other = valid_other_temp[feature_columns], valid_other_temp[target_column]

# 学習
est_busy = GradientBoostingRegressor(random_state = 1192).fit(X_train_busy, y_train_busy)
est_other = GradientBoostingRegressor(random_state = 1192).fit(X_train_other, y_train_other)


# 予測(対数変換を逆変換する)
y_pred_train_busy = np.exp(est.predict(X_train_busy) + train_busy_temp["y_prophet"])
y_pred_valid_busy = np.exp(est.predict(X_valid_busy) + valid_busy_temp["y_prophet"])

y_pred_train_other = np.exp(est.predict(X_train_other) + train_other_temp["y_prophet"])
y_pred_valid_other = np.exp(est.predict(X_valid_other) + valid_other_temp["y_prophet"])


# 予測精度の確認
# 小数第7位はコンペスコアの有効数字
print("繁忙期の訓練データの評価関数:", np.round(mean_absolute_error(train_busy_temp["y"], y_pred_train_busy), decimals = 7))
print("繁忙期の評価データの評価関数:", np.round(mean_absolute_error(valid_busy_temp["y"], y_pred_valid_busy), decimals = 7))
print("その他の時期の訓練データの評価関数:", np.round(mean_absolute_error(train_other_temp["y"], y_pred_train_other), decimals = 7))
print("その他の時期の評価データの評価関数:", np.round(mean_absolute_error(valid_other_temp["y"], y_pred_valid_other), decimals = 7))



# 予測結果の確認
fig, axes = plt.subplots(
    nrows = 2, ncols = 2, # axの縦・横の数
    height_ratios = [1, 1], width_ratios = [2, 1], # ax の縦・横比
    figsize = (15, 8)
)

# 描画
g_time_train = sns.lineplot(data = train, x = "datetime", y = "y", ax = axes[0, 0])
#g_predict_train_busy = sns.lineplot(x = train_busy_temp["datetime"], y = y_pred_train_busy, ax = axes[0, 0])
g_predict_valid_busy = sns.lineplot(x = valid_busy_temp["datetime"], y = y_pred_valid_busy, ax = axes[0, 0])

#g_predict_train_other = sns.lineplot(x = train_other_temp["datetime"], y = y_pred_train_other, ax = axes[0, 0])
g_predict_valid_other = sns.lineplot(x = valid_other_temp["datetime"], y = y_pred_valid_other, ax = axes[0, 0])


g_hist_train = sns.histplot(data = train, x = "y", ax = axes[0, 1])
#g_predict_hist_train_busy = sns.histplot(x = y_pred_train_busy, ax = axes[0, 1])
g_predict_hist_valid_busy = sns.histplot(x = y_pred_valid_busy, ax = axes[0, 1])
#g_predict_hist_train_other = sns.histplot(x = y_pred_train_other, ax = axes[0, 1])
g_predict_hist_valid_other = sns.histplot(x = y_pred_valid_other, ax = axes[0, 1])


# 残差
g_residual_dummy = sns.scatterplot(x = [date(2011, 1, 1)], y = 0, marker = "+", ax = axes[1, 0])
#g_residual_train_busy = sns.scatterplot(x = train_busy_temp["datetime"], y = y_pred_train_busy - train_busy_temp["y"], marker = "+", ax = axes[1, 0])
g_residual_valid_busy = sns.scatterplot(x = valid_busy_temp["datetime"], y = y_pred_valid_busy - valid_busy_temp["y"], marker = "+", ax = axes[1, 0])
#g_residual_train_other = sns.scatterplot(x = train_other_temp["datetime"], y = y_pred_train_other - train_other_temp["y"], marker = "+", ax = axes[1, 0])
g_residual_valid_other = sns.scatterplot(x = valid_other_temp["datetime"], y = y_pred_valid_other - valid_other_temp["y"], marker = "+", ax = axes[1, 0])

g_residual_hist_dummy = sns.histplot(x = [0], ax = axes[1, 1])
#g_residual_hist_train_busy = sns.histplot(x = y_pred_train_busy - train_busy_temp["y"], ax = axes[1, 1])
g_residual_hist_valid_busy = sns.histplot(x = y_pred_valid_busy - valid_busy_temp["y"], ax = axes[1, 1])
#g_residual_hist_train_other = sns.histplot(x = y_pred_train_other - train_other_temp["y"], ax = axes[1, 1])
g_residual_hist_valid_other = sns.histplot(x = y_pred_valid_other - valid_other_temp["y"], ax = axes[1, 1])

# 調整
plt.setp(g_time_train.get_xticklabels(), rotation = 90)
plt.setp(g_time_train, ylim = (0, 120))

plt.suptitle("引越し数 y の予測精度の確認")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

# 特徴量の重要度
df_feature_importance = pl.DataFrame({
    "feature": est.feature_names_in_,
    "importance": est.feature_importances_
})
g_importance = sns.barplot(data = df_feature_importance, x = "importance", y = "feature")
plt.setp(g_importance, title = "特徴量の重要度")

繁忙期の訓練データの評価関数: 5.5665459
繁忙期の評価データの評価関数: 5.9653361
その他の時期の訓練データの評価関数: 4.7250892
その他の時期の評価データの評価関数: 4.5285439

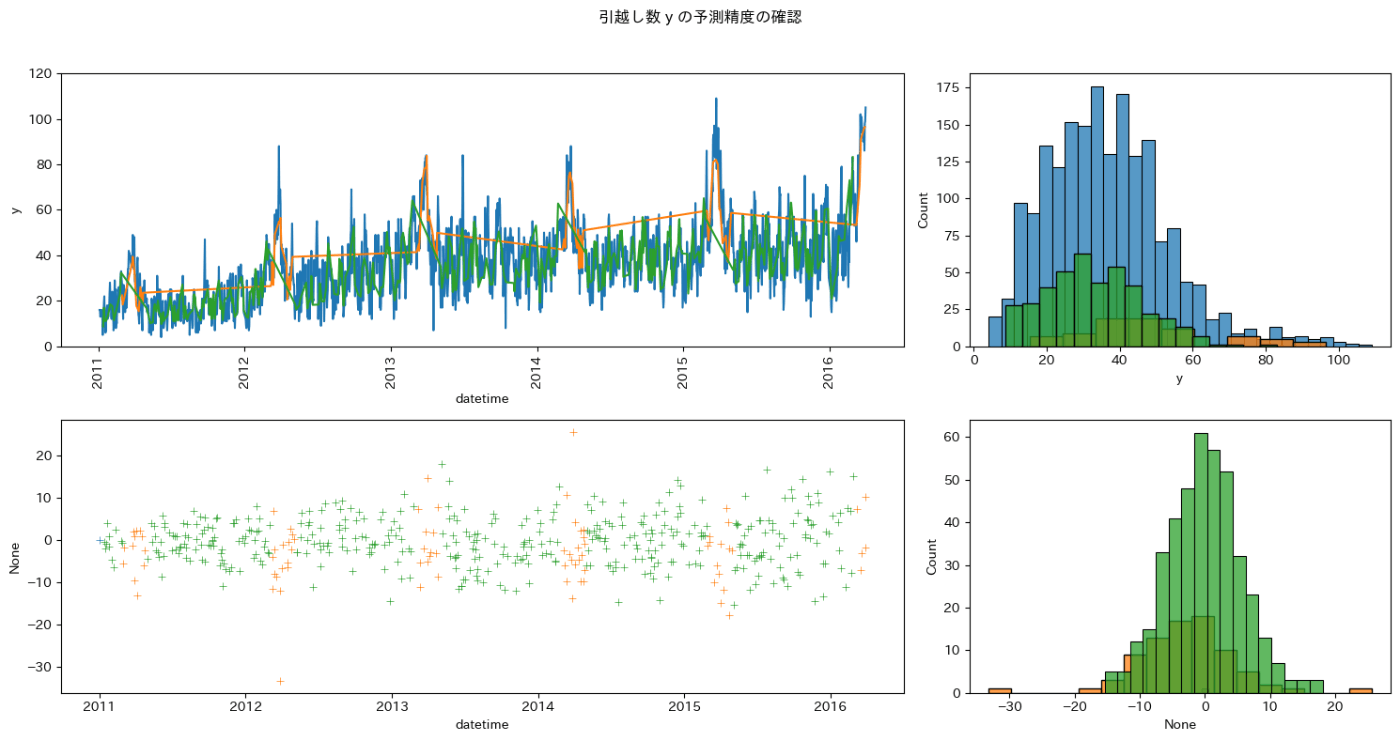
データを分割しても、繁忙期の予測精度は改善しませんでした。
全体的な予測精度は分割しない方が良かったです。
今後はデータ分割無しでいきます。

次は、重要度の低い特徴量を削除したモデルを試します。

低重要度削除

予測への寄与度が低い特徴量(client、
quarter_satrt、
quarter_end、
month_start、
month_end、
gw、
obon)を削除して学習します。

# 機械学習ライブラリと親和性の高いPandasに変換する
train_pandas = train.to_pandas().set_index("id")

# 目的変数と特徴量
target_column = "y_difference"
feature_columns = [
    #'client',
    'price_am', 'price_pm',
    'year', 'quarter', 'month', 'week', 'ordinal_day', 'week_of_month', 'day', 'day_of_week',
    #'quarter_start', 'quarter_end', 'month_start', 'month_end',
    'price_sum', 'price_difference', 'price_product',
    'holiday',
    #'gw', 'obon',
    'sw', 'sat_sun'
 ]

# 訓練データと評価データに分割するマスク
np.random.seed(1192)
train_mask_1 = np.random.choice([True, False], size = len(train_pandas), p = [0.75, 0.25])

# 説明変数、目的変数の分割
train_temp, valid_temp = train_pandas[train_mask_1], train_pandas[~train_mask_1]
X_train, y_train = train_temp[feature_columns], train_temp[target_column]
X_valid, y_valid = valid_temp[feature_columns], valid_temp[target_column]

# 学習
est = GradientBoostingRegressor(random_state = 1192).fit(X_train, y_train)

# 予測(対数変換を逆変換する)
y_pred_train = np.exp(est.predict(X_train) + train_temp["y_prophet"])
y_pred_valid = np.exp(est.predict(X_valid) + valid_temp["y_prophet"])


# 予測精度の確認
print("訓練データの評価関数:", np.round(mean_absolute_error(train_temp["y"], y_pred_train), decimals = 7))# 小数第7位はコンペスコアの有効数字
print("評価データの評価関数:", np.round(mean_absolute_error(valid_temp["y"], y_pred_valid), decimals = 7))

# 予測結果の確認
fig, axes = plt.subplots(
    nrows = 2, ncols = 2, # axの縦・横の数
    height_ratios = [1, 1], width_ratios = [2, 1], # ax の縦・横比
    figsize = (15, 8)
)

# 描画
g_time_train = sns.lineplot(data = train, x = "datetime", y = "y", ax = axes[0, 0])
g_predict_train = sns.lineplot(x = train_temp["datetime"], y = y_pred_train, ax = axes[0, 0])
g_predict_valid = sns.lineplot(x = valid_temp["datetime"], y = y_pred_valid, ax = axes[0, 0])

g_hist_train = sns.histplot(data = train, x = "y", ax = axes[0, 1])
g_predict_hist_train = sns.histplot(x = y_pred_train, ax = axes[0, 1])
g_predict_hist_valid = sns.histplot(x = y_pred_valid, ax = axes[0, 1])

# 残差
g_residual_dummy = sns.scatterplot(x = [date(2011, 1, 1)], y = 0, marker = "+", ax = axes[1, 0])
g_residual_train = sns.scatterplot(x = train_temp["datetime"], y = y_pred_train - train_temp["y"], marker = "+", ax = axes[1, 0])
g_residual_valid = sns.scatterplot(x = valid_temp["datetime"], y = y_pred_valid - valid_temp["y"], marker = "+", ax = axes[1, 0])

g_residual_hist_dummy = sns.histplot(x = [0], ax = axes[1, 1])
g_residual_hist_train = sns.histplot(x = y_pred_train - train_temp["y"], ax = axes[1, 1])
g_residual_hist_valid = sns.histplot(x = y_pred_valid - valid_temp["y"], ax = axes[1, 1])


# 調整
plt.setp(g_time_train.get_xticklabels(), rotation = 90)
plt.setp(g_time_train, ylim = (0, 120))

plt.suptitle("引越し数 y の予測精度の確認")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

# 特徴量の重要度
df_feature_importance = pl.DataFrame({
    "feature": est.feature_names_in_,
    "importance": est.feature_importances_
})
g_importance = sns.barplot(data = df_feature_importance, x = "importance", y = "feature")
plt.setp(g_importance, title = "特徴量の重要度")

訓練データの評価関数: 4.7307091
評価データの評価関数: 5.201249

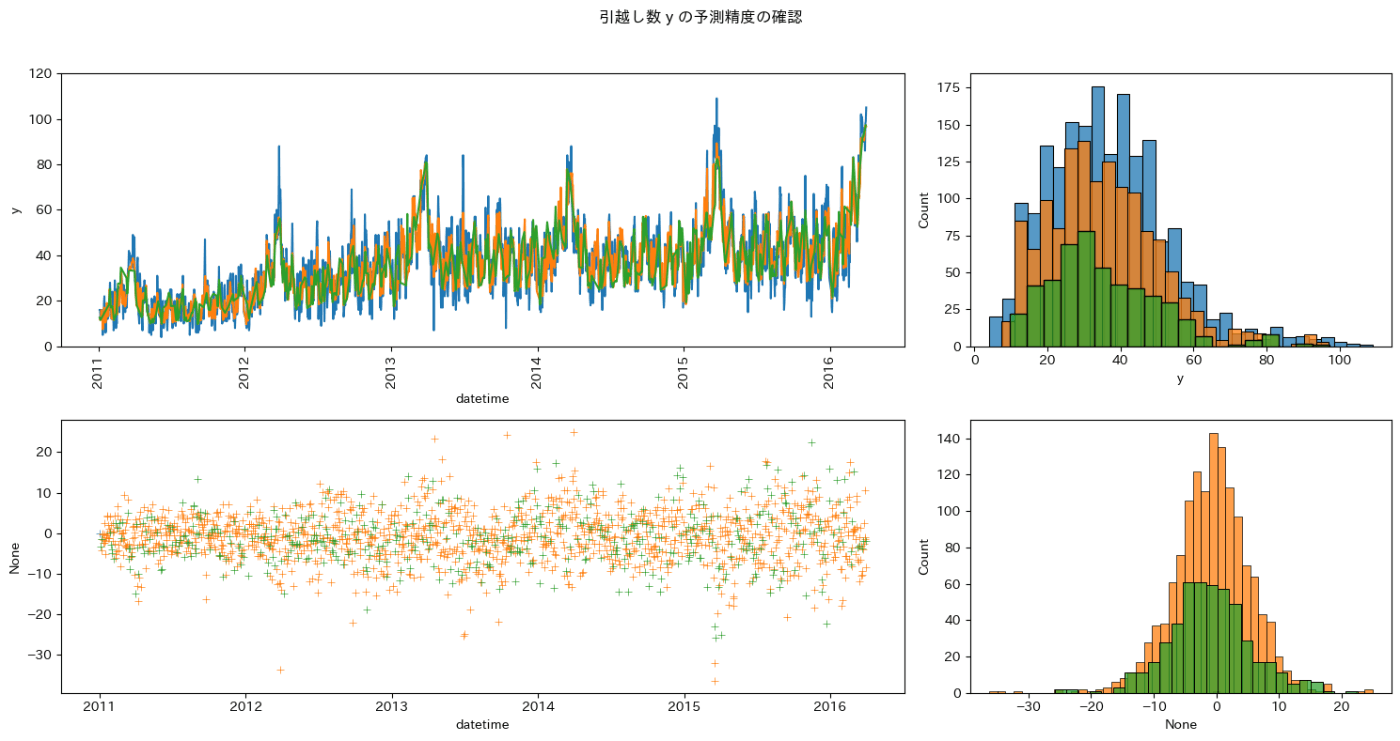
寄与度の低い特徴量を削除して、モデルを多少シンプルにしても精度が変わらないことを確認しました。

与えられた特徴量のみ

訓練データの評価関数: 7.0583736
評価データの評価関数: 7.1578642

特徴量追加

訓練データの評価関数: 4.7227557
評価データの評価関数: 5.2050808

低寄与度の特徴量削除

訓練データの評価関数: 4.7307091
評価データの評価関数: 5.201249

ハイパーパラメータ最適化

# 機械学習ライブラリと親和性の高いPandasに変換する
train_pandas = train.to_pandas().set_index("id")

# 目的変数と特徴量
target_column = "y_difference"
feature_columns = [
    #'client',
    'price_am', 'price_pm',
    'year', 'quarter', 'month', 'week', 'ordinal_day', 'week_of_month', 'day', 'day_of_week',
    #'quarter_start', 'quarter_end', 'month_start', 'month_end',
    'price_sum', 'price_difference', 'price_product',
    'holiday',
    #'gw', 'obon',
    'sw', 'sat_sun'
 ]

# 訓練データと評価データに分割するマスク
np.random.seed(1192)
train_mask_1 = np.random.choice([True, False], size = len(train_pandas), p = [0.75, 0.25])

# 説明変数、目的変数の分割
train_temp, valid_temp = train_pandas[train_mask_1], train_pandas[~train_mask_1]
X_train, y_train = train_temp[feature_columns], train_temp[target_column]
X_valid, y_valid = valid_temp[feature_columns], valid_temp[target_column]

# ハイパーパラメータ最適化時の評価関数
scoring = make_scorer(r2_score, response_method = "predict", greater_is_better = True)

# 推定器
est = GradientBoostingRegressor()

# 交差検証器
rkf = RepeatedKFold(n_splits = 4, n_repeats = 20, random_state = 1192)

# ハイパーパラメータ
param_distributions = {
    "loss": ["squared_error", "absolute_error", "huber"],
    "learning_rate": np.linspace(0.1, 0.2, num = 5, endpoint = True, dtype = float),
    "n_estimators": np.linspace(10, 255, num = 100, endpoint = True, dtype = int),
    "subsample": np.linspace(0.5, 1, num = 10, endpoint = True, dtype = float),
    "criterion": ["friedman_mse", "squared_error"],
    "min_samples_split": np.linspace(2, 50, num = 10, endpoint = True, dtype = int),
    "min_weight_fraction_leaf": np.linspace(0, 0.5, num = 5, endpoint = True, dtype = float),
    "max_depth": np.linspace(1, 20, num = 5, endpoint = True, dtype = int),
    "max_features": ["sqrt", "log2", None],
    "validation_fraction": np.linspace(0.1, 0.5, num = 10, endpoint = True, dtype = float),
    "random_state": [1192, 765, 961, 876, 346, 315, 283],
}

# 最終推定器
search = HalvingRandomSearchCV(
    est,
    param_distributions = param_distributions,
    cv = rkf,
    scoring = scoring,
    return_train_score = True,
    random_state = 0
    ).fit(X_train, y_train)
print("最適ハイパーパラメータ", search.best_params_)


# 予測(対数変換を逆変換する)
y_pred_train = np.exp(search.predict(X_train) + train_temp["y_prophet"])
y_pred_valid = np.exp(search.predict(X_valid) + valid_temp["y_prophet"])


# 予測精度の確認
print("訓練データの評価関数:", np.round(mean_absolute_error(train_temp["y"], y_pred_train), decimals = 7))# 小数第7位はコンペスコアの有効数字
print("評価データの評価関数:", np.round(mean_absolute_error(valid_temp["y"], y_pred_valid), decimals = 7))

# 予測結果の確認
fig, axes = plt.subplots(
    nrows = 2, ncols = 2, # axの縦・横の数
    height_ratios = [1, 1], width_ratios = [2, 1], # ax の縦・横比
    figsize = (15, 8)
)

# 描画
g_time_train = sns.lineplot(data = train, x = "datetime", y = "y", ax = axes[0, 0])
g_predict_train = sns.lineplot(x = train_temp["datetime"], y = y_pred_train, ax = axes[0, 0])
g_predict_valid = sns.lineplot(x = valid_temp["datetime"], y = y_pred_valid, ax = axes[0, 0])

g_hist_train = sns.histplot(data = train, x = "y", ax = axes[0, 1])
g_predict_hist_train = sns.histplot(x = y_pred_train, ax = axes[0, 1])
g_predict_hist_valid = sns.histplot(x = y_pred_valid, ax = axes[0, 1])

# 残差
g_residual_dummy = sns.scatterplot(x = [date(2011, 1, 1)], y = 0, marker = "+", ax = axes[1, 0])
g_residual_train = sns.scatterplot(x = train_temp["datetime"], y = y_pred_train - train_temp["y"], marker = "+", ax = axes[1, 0])
g_residual_valid = sns.scatterplot(x = valid_temp["datetime"], y = y_pred_valid - valid_temp["y"], marker = "+", ax = axes[1, 0])

g_residual_hist_dummy = sns.histplot(x = [0], ax = axes[1, 1])
g_residual_hist_train = sns.histplot(x = y_pred_train - train_temp["y"], ax = axes[1, 1])
g_residual_hist_valid = sns.histplot(x = y_pred_valid - valid_temp["y"], ax = axes[1, 1])


# 調整
plt.setp(g_time_train.get_xticklabels(), rotation = 90)
plt.setp(g_time_train, ylim = (0, 120))

plt.suptitle("引越し数 y の予測精度の確認")
plt.tight_layout(rect = [0, 0, 1, 0.96])# 余白の調整  
plt.show()

# 特徴量の重要度
#df_feature_importance = pl.DataFrame({
#    "feature": est.feature_names_in_,
#    "importance": est.feature_importances_
#})
#g_importance = sns.barplot(data = df_feature_importance, x = "importance", y = "feature")
#plt.setp(g_importance, title = "特徴量の重要度")

最適ハイパーパラメータ {'validation_fraction': 0.14444444444444446, 'subsample': 1.0, 'random_state': 346, 'n_estimators': 165, 'min_weight_fraction_leaf': 0.125, 'min_samples_split': 50, 'max_features': None, 'max_depth': 10, 'loss': 'absolute_error', 'learning_rate': 0.15000000000000002, 'criterion': 'friedman_mse'}
訓練データの評価関数: 5.0156345
評価データの評価関数: 5.2403612

スコアは悪化しましたが、訓練データと評価データのスコアがほぼ同じであるため、汎化性能の高い推定器を学習できました。
引越し数分布の裾野の予測が今後の課題です。
それなりの精度のモデルを作製できたので、テストデータの目的変数を算出して提出ファイルを作成します。

与えられた特徴量のみ

訓練データの評価関数: 7.0583736
評価データの評価関数: 7.1578642

特徴量追加

訓練データの評価関数: 4.7227557
評価データの評価関数: 5.2050808

低寄与度の特徴量削除

訓練データの評価関数: 4.7307091
評価データの評価関数: 5.201249

ハイパーパラメータ最適化

訓練データの評価関数: 5.0156345
評価データの評価関数: 5.2403612

テストデータの予測

# 機械学習ライブラリと親和性の高いPandasに変換する
test_pandas = test.to_pandas().set_index("id")

# 説明変数の分割
X_test = test_pandas[feature_columns]

# 予測(対数変換を逆変換する)
y_pred_train = np.exp(search.predict(X_test) + test_pandas["y_prophet"])

# 提出DataFrame
submit = pl.DataFrame({
    "id": X_test.index.values,
    "y": y_pred_train.values,
})
# close = 1 のデータと連結する
submit = pl.concat(
    [submit, test_close],
    how = "vertical_relaxed"
).sort("id")

# 提出ファイルを保存する
#submit.write_csv("../data/output/submit.csv", include_header = False)

使用ライブラリ

%load_ext watermark
%watermark -n -u -v -iv -w

Last updated: Sat Jun 15 2024

Python implementation: CPython
Python version       : 3.11.9
IPython version      : 8.25.0

sklearn            : 1.5.0
numpy              : 1.26.4
polars             : 0.20.31
matplotlib         : 3.8.4
jpholiday          : 0.1.10
seaborn            : 0.13.2
japanize_matplotlib: 1.1.3

Watermark: 2.4.3

おわりに

この記事では次のことを行いました。

1. EDAで目的変数の分布の特徴を掴み、目的変数の分布が年々右側にシフトしていることを発見した。
2. 引越し数が0となる休業日のデータを分離して、モデルの汎化性能を上げた。
3. Prophetで年毎の目的変数の分布を揃えた、すなわち過去のデータと未来のデータの目的変数の分布を揃えて機械学習で予測できるようにした。
4. Scikit-Learnの勾配ブースティング木推定器で目的変数を予測した。
5. 特徴量作成、ハイパーパラメータ最適化で予測精度と汎化性能を改善した。

本コンペでの一番の収穫は、過去のデータと未来のデータの目的変数の分布を揃えて機械学習で予測できるようにすることで、ビジネスの実データを上手く分析できると分かったことです。
今後実データを扱うときの助けになることを確信しました。

乱文ではありましたが、本記事が読者の方々の参考になれば幸いです。

課題

1. 目的変数の分布の裾野を予測できる特徴量の探索
2. 特徴量同士の相関(他にも無駄な特徴量はあるか? 主成分と目的変数の相関は?)
3. LBに近いローカルCVの構築
4. Prophetのアルゴリズムやほかの機能(季節性)の勉強
5. Prophet、Scikit-Learn以外のモデルとの比較(LightGBM、XGBoost、CatBoost、AutoGloun等)
6. 汎化性能の高いハイパーパラメータ最適化(Optuna)
7. コンペの参考URLの活用
   • https://signate.jp/competitions/269#Other
   • https://www.pbn.jp/rent_trand/
   • https://www.jpm.jp/marketdata/
   • http://www.e-stat.go.jp/SG1/estat/OtherList.do?bid=000001006005&cycode=1
   • http://www.e-stat.go.jp/SG1/estat/OtherList.do?bid=000000110001&cycode=1
   • http://www.e-stat.go.jp/SG1/estat/NewList.do?tid=000001028897