MT法が上手くいくデータセット/そうではないもの(品質工学)
はじめに
MT法とはマハラノビス距離に基づくパターン認識の手法です。
ニューラルネットワークなどに比べて軽量な仕組みのため、異常検査装置のような組込みプログラミングにはMT法の方が向いています。
パラメトリックな解釈が可能なため、MT法が適しているデータセットの特徴がはっきりしています。
この記事では、MT法が上手くいく場合とそうでない場合をPythonコードで紹介します。
参考
- 立林 和夫, 手島 昌一, 長谷川 良子. 入門 MTシステム入門. 日科技連出版社. 2008/12/1.
結論
MT法が上手く行くのは、特徴量
すなわち線形な相関関係から外れた特徴量を外れ値として判断します。
PythonのPandasでは行ベクトルを基本としているため、この記事でもそれに倣います。
参考
Pythonの準備
ライブラリのインポートや、MT法の自作クラスを準備します。
使用するライブラリのインポート
ライブラリのインポート
# ---- ライブラリをimportする ----
# ---- DataFrameライブラリをimportする ----
import polars as pl
import polars.selectors as cs
#import pandas as pd
import numpy as np
# ---- DataFrameの設定を初期化する ----
pl.Config(fmt_str_lengths = 100, tbl_cols = 100, tbl_rows = 10)
np.set_printoptions(precision = 3, floatmode = 'fixed')
#pd.set_option('display.max_columns', 100)
#pd.set_option('display.max_rows', 100)
# ---- プロットライブラリをimportする ----
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
# ※日本語でプロットしたい場合、英語フォントはコメントアウトする
import japanize_matplotlib
#plt.rcParams['font.family'] = 'Times New Roman'
# ---- プロットの設定を初期化する ----
plt.rcParams['mathtext.fontset'] = 'stix'
plt.rcParams["font.size"] = 15
plt.rcParams['xtick.labelsize'] = 10
plt.rcParams['ytick.labelsize'] = 10
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'
plt.rcParams['axes.linewidth'] = 1.0
plt.rcParams['axes.grid'] = True
# ---- 機械学習ライブラリをimportする ----
# 自作推定器のベースクラス
from sklearn.base import BaseEstimator, ClassifierMixin
MT法クラスを定義する
自作クラスを定義します。
クラス分類、MD値、Zスコアなどいくつかの機能を持たせています。
MT法の自作クラス
# ---- MT法に基づいて判定する自作推定器 ----
class MahalanobisTaguchiMethod(BaseEstimator, ClassifierMixin):
# ---- 初期化 ----
# threshold: MT法の閾値
def __init__(self, *, threshold = 4):
# ---- MD値の閾値 ----
self.threshold = threshold
# ---- モデルパラメータ ----
self.mean = None
self.covariance = None
self.inverse_covariance = None
# ---- Zスコアを計算するためのパラメータ ----
self.std = None
# ---- モデルを学習させる ----
# X: 計画行列
# y: 目的変数。MT法は良品のみ学習させるため不要。
def fit(self, X, y = None):
# ---- 学習済みフラグをONにする ----
self.is_fitted_ = True
# ---- モデルパラメータを更新する ----
self.mean = np.mean(X, axis = 0)
self.covariance = np.cov(X.T)
self.inverse_covariance = np.linalg.inv(self.covariance)
# ---- Zスコアを計算するためのパラメータを更新する ----
self.std = np.std(X, axis = 0)
return self
# ---- MD値に基づいて基準空間に属するかを判定する ----
# X: 計画行列
def predict(self, X):
# ---- MD値を計算する ----
X_scaled = X - self.mean
k = X.shape[1]
md = np.sum(np.dot(X_scaled, self.inverse_covariance) * X_scaled, axis = 1) / k
# ---- データが基準空間に属するかを判定する ----
pred = np.zeros(X.shape[0])
pred[md < self.threshold] = 1
# ---- 判定値を返す ----
return pred
# ---- MD値を計算する ----
# X: 計画行列
def mahalanobis_distance(self, X):
# ---- MD値を計算する ----
X_scaled = X - self.mean
k = X.shape[1]
md = np.sum(np.dot(X_scaled, self.inverse_covariance) * X_scaled, axis = 1) / k
return md
# ---- Zスコアを計算する ----
# X: 計画行列
def z_score(self, X):
# ---- Zスコアを計算する ----
X_scaled = X - self.mean
z_score = X_scaled / self.std
return z_score
# ---- 学習用データの平均値を返す ----
def get_mean(self):
return np.copy(self.mean) if self.is_fitted_ else None
# ---- 学習用データの共分散行列を返す ----
def get_covariance(self):
return np.copy(self.covariance) if self.is_fitted_ else None
# ---- 学習用データの共分散行列の逆行列を返す ----
def get_inverse_covariance(self):
return np.copy(self.inverse_covariance) if self.is_fitted_ else None
# ---- 学習用データの標準偏差を返す ----
def get_mean(self):
return np.copy(self.std) if self.is_fitted_ else None
実験
複数のデータセットを使って、MT法が上手くいく条件を確認します。
1. MT法が上手くいく場合
最初にMT法が上手くいくデータセットで実験します。
学習用データは直線の相関関係があります。
MT法が上手くいくデータセットを作成する関数
# ---- 直線の相関関係のある2次元のデータセットを作成する ----
# このデータセットはMT法が上手くいく
def make_dataset_linear_2d():
# ---- 相関関係 ax+b のパラメータを設定する ----
a = 2
b = 1
b_ng = 6
# ---- 乱数のパラメータを設定する
loc_0 = 0.0
scale_0 = 2.0
loc_1 = 0.0
scale_1 = 1.0
# ---- 学習用データを作成する ----
np.random.seed(42)
train = (
pl.DataFrame({
"x0": np.random.normal(loc = loc_0, scale = scale_0, size = 32),
"x1": np.random.normal(loc = loc_1, scale = 1.0, size = 32),
})
.with_columns(
(a * pl.col("x0") + b + pl.col("x1")).alias("x1")
)
.to_pandas()
)
# ---- 基準空間に属する評価用データを作成する ----
np.random.seed(43)
valid_ok = (
pl.DataFrame({
"x0": np.random.normal(loc = loc_0, scale = scale_0, size = 5),
"x1": np.random.normal(loc = loc_1, scale = 1.0, size = 5),
})
.with_columns(
(a * pl.col("x0") + b + pl.col("x1")).alias("x1")
)
.to_pandas()
)
# ---- 基準空間に属さない評価用データを作成する ----
np.random.seed(44)
valid_ng = (
pl.DataFrame({
"x0": np.random.normal(loc = loc_0, scale = scale_0, size = 5),
"x1": np.random.normal(loc = loc_1, scale = 1.0, size = 5),
})
.with_columns(
(a * pl.col("x0") + b_ng + pl.col("x1")).alias("x1")
)
.to_pandas()
)
# ---- 学習用データ、基準空間に属する評価用データ、属さない評価用データを返す
return train, valid_ok, valid_ng
それぞれのデータセットの生データを表示します。
いずれも x0 が大きくなると x1 も大きくなっているように見えます。
データセットを作成する
# ---- データセットを作成する ----
train, valid_ok, valid_ng = make_dataset_linear_2d()
display(train.head())
display(valid_ok)
display(valid_ng)

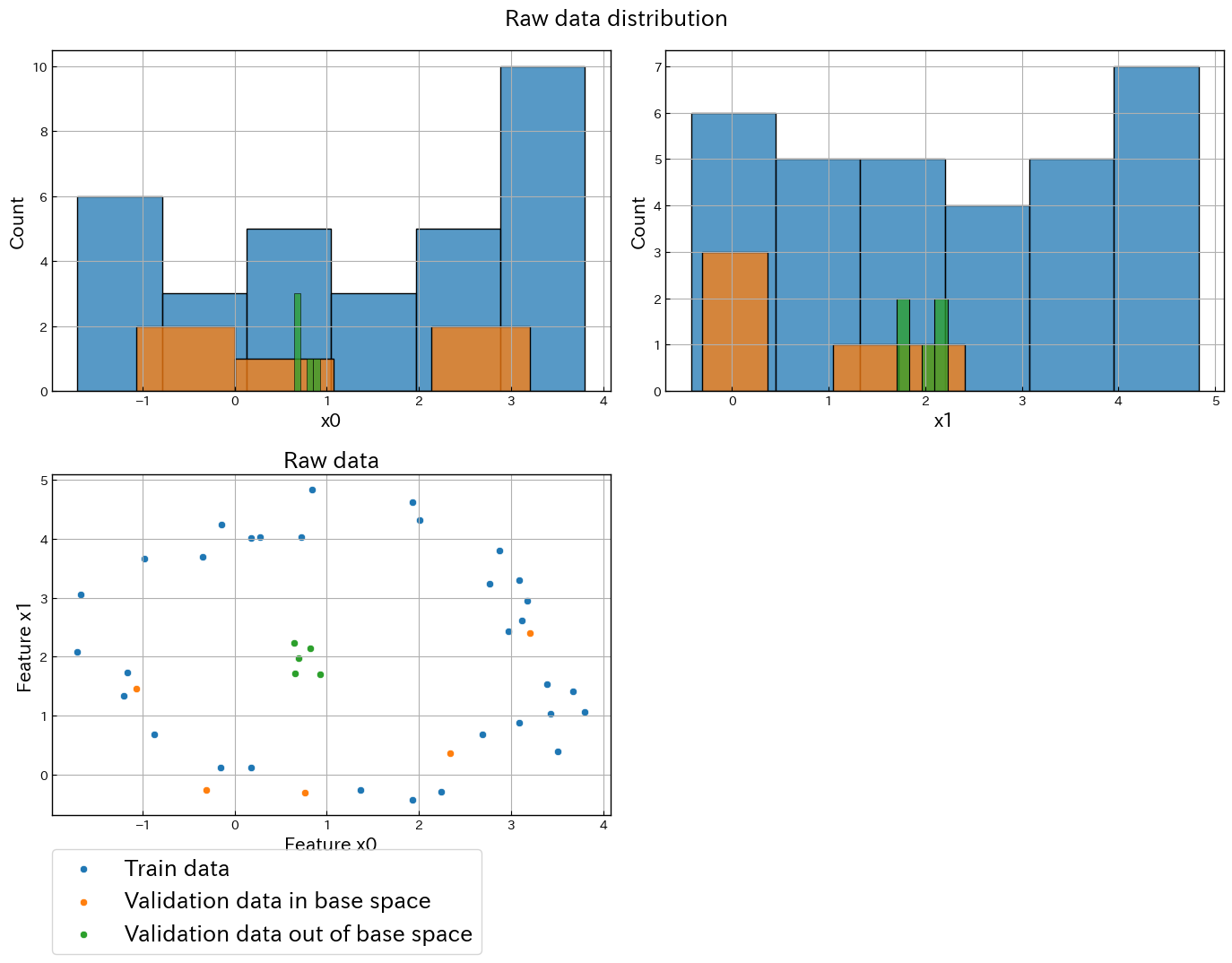
各データセットの値をプロットします。
散布図を見ると3つのデータセットには直線の相関関係があり、基準空間外のデータは別の直線上にあることが分かります。
各特徴量のヒストグラムからは基準空間外のデータを分離する方法は出てこないでしょう。
このように直線の相関関係から外れた値が外れ値の場合、MT法で上手く分離することができます。
生データの分布
# ---- 生データの分布をプロットする ----
# パレット数
row_count = 2
column_count = 2
# Figure
fig = plt.figure(figsize = (6 * row_count + 2, 5 * column_count + 1))# (横, 縦)
# カラーマップ
cmap = plt.get_cmap("tab10")
# x0のプロット
ax_x0 = fig.add_subplot(row_count, column_count, 1)
sns.histplot(data = train, x = "x0", color = cmap(0), ax = ax_x0)
sns.histplot(data = valid_ok, x = "x0", color = cmap(1), ax = ax_x0)
sns.histplot(data = valid_ng, x = "x0", color = cmap(2), ax = ax_x0)
# x1のプロット
ax_x1 = fig.add_subplot(row_count, column_count, 2)
sns.histplot(data = train, x = "x1", color = cmap(0), ax = ax_x1)
sns.histplot(data = valid_ok, x = "x1", color = cmap(1), ax = ax_x1)
sns.histplot(data = valid_ng, x = "x1", color = cmap(2), ax = ax_x1)
# x0 と x1 の散布図
ax_scatter = fig.add_subplot(row_count, column_count, 3)
sns.scatterplot(data = train, x = "x0", y = "x1", ax = ax_scatter, color = cmap(0), label = "Train data")
sns.scatterplot(data = valid_ok, x = "x0", y = "x1", ax = ax_scatter, color = cmap(1), label = "Validation data in base space")
sns.scatterplot(data = valid_ng, x = "x0", y = "x1", ax = ax_scatter, color = cmap(2), label = "Validation data out of base space")
plt.setp(ax_scatter, title = "Raw data", xlabel = "Feature x0", ylabel = "Feature x1")
plt.suptitle("Raw data distribution")
plt.tight_layout()
plt.show()

このデータセットをMT法で分離できるか試してみましょう。
MT法の分類
# ---- MT法のモデルを学習させる ----
model = MahalanobisTaguchiMethod(threshold = 4).fit(X = train)
# ---- 各データのマハラノビス距離を計算する ----
md_train = model.mahalanobis_distance(train)
md_valid_ok = model.mahalanobis_distance(valid_ok)
md_valid_ng = model.mahalanobis_distance(valid_ng)
# ---- 特徴量のヒストグラムと、生データとマハラノビス距離の散布図をプロットする ----
# パレット数
row_count = 2
column_count = 2
# Figure
fig = plt.figure(figsize = (6 * row_count + 2, 5 * column_count + 1))# (横, 縦)
# カラーマップ
cmap = plt.get_cmap("tab10")
# x0のプロット
ax_x0 = fig.add_subplot(row_count, column_count, 1)
sns.histplot(data = train, x = "x0", color = cmap(0), ax = ax_x0)
sns.histplot(data = valid_ok, x = "x0", color = cmap(1), ax = ax_x0)
sns.histplot(data = valid_ng, x = "x0", color = cmap(2), ax = ax_x0)
# x1のプロット
ax_x1 = fig.add_subplot(row_count, column_count, 2)
sns.histplot(data = train, x = "x1", color = cmap(0), ax = ax_x1)
sns.histplot(data = valid_ok, x = "x1", color = cmap(1), ax = ax_x1)
sns.histplot(data = valid_ng, x = "x1", color = cmap(2), ax = ax_x1)
# x0 とマハラノビス距離の散布図
ax_x0_md = fig.add_subplot(row_count, column_count, 3)
sns.scatterplot(x = train["x0"], y = md_train, color = cmap(0), ax = ax_x0_md)
sns.scatterplot(x = valid_ok["x0"], y = md_valid_ok, color = cmap(1), ax = ax_x0_md)
sns.scatterplot(x = valid_ng["x0"], y = md_valid_ng, color = cmap(2), ax = ax_x0_md)
plt.setp(ax_x0_md, yticks = [0, 4], ylabel = "Mahalanobis Distance")
# x1 とマハラノビス距離の散布図
ax_x1_md = fig.add_subplot(row_count, column_count, 4)
sns.scatterplot(x = train["x1"], y = md_train, color = cmap(0), ax = ax_x1_md, label = "Train data")
sns.scatterplot(x = valid_ok["x1"], y = md_valid_ok, color = cmap(1), ax = ax_x1_md, label = "Validation data in base space")
sns.scatterplot(x = valid_ng["x1"], y = md_valid_ng, color = cmap(2), ax = ax_x1_md, label = "Validation data out of base space")
plt.setp(ax_x1_md, yticks = [0, 4], ylabel = "Mahalanobis Distance")
ax_x1_md.legend(bbox_to_anchor=(0, -0.1), loc='upper left', borderaxespad=0, fontsize=18)
plt.suptitle("Compare Raw data distribution and Mahalanobis distance")
plt.tight_layout()
plt.show()
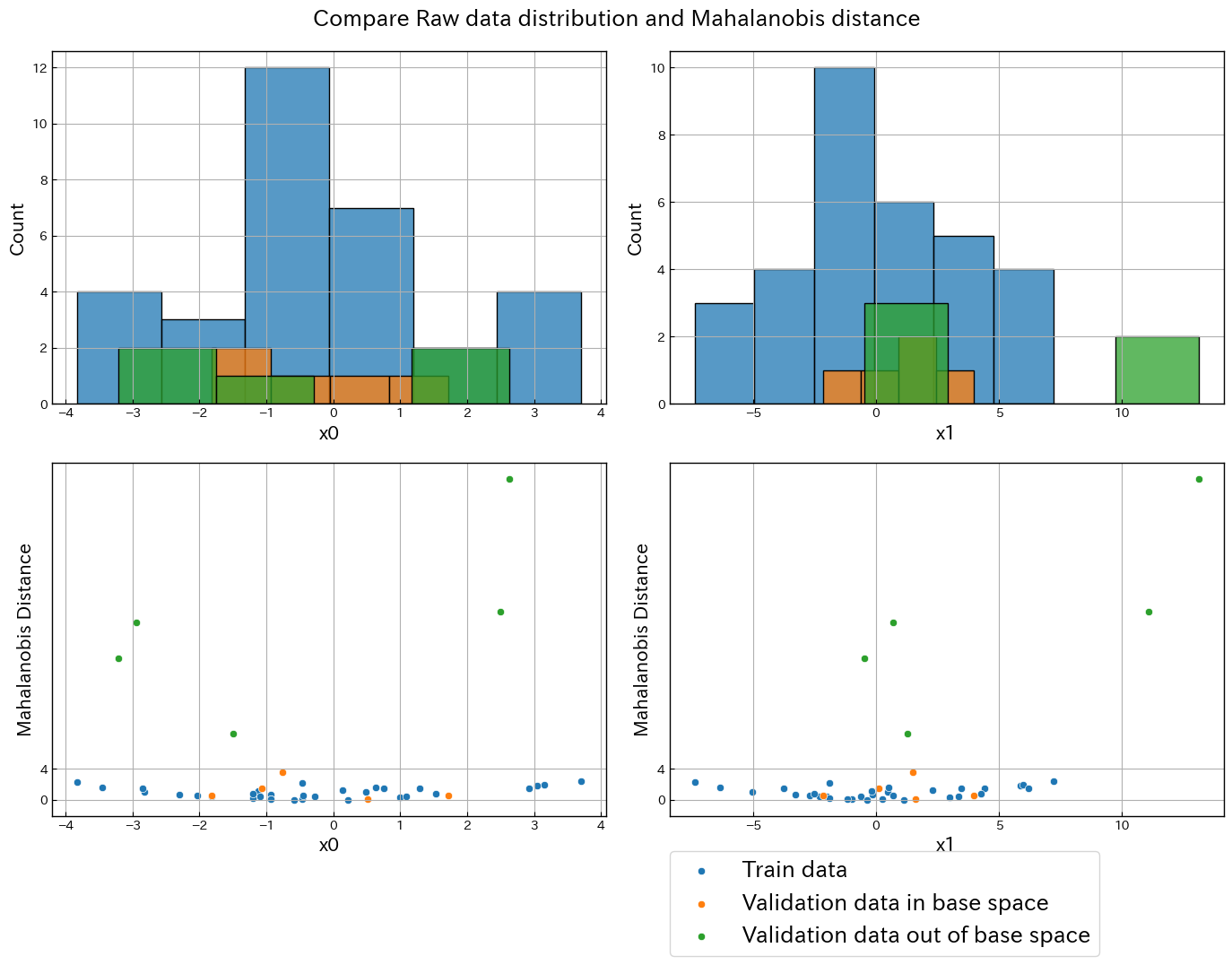
評価用データに1個ギリギリなものがありますが、正しく分類できました。
2. MT法が上手くいかない場合
MT方が苦手な場合も確認しましょう。
円弧の相関関係のある2次元のデータセットを作成する関数
# ---- 円弧の相関関係のある2次元のデータセットを作成する ----
# このデータセットはMT法が上手くいかない
def make_dataset_circle_2d():
# ---- 相関関係 (x, y) = (r cosθ + p, r sinθ + q) のパラメータを設定する ----
r_min = 2
r_max = 3
p = 1
q = 2
r_min_ng = 0.2
r_max_ng = 0.5
# ---- 学習用データを作成する ----
np.random.seed(42)
train = (
pl.DataFrame({
"r": np.random.uniform(low = r_min, high = r_max, size = 32),
"θ": np.random.uniform(low = 0, high = 2 * np.pi, size = 32),
})
.with_columns([
(pl.col("r") * pl.col("θ").cos() + p).alias("x0"),
(pl.col("r") * pl.col("θ").sin() + q).alias("x1"),
])
.drop(["r", "θ"])
.to_pandas()
)
# ---- 基準空間に属する評価用データを作成する ----
np.random.seed(43)
valid_ok = (
pl.DataFrame({
"r": np.random.uniform(low = r_min, high = r_max, size = 5),
"θ": np.random.uniform(low = 0, high = 2 * np.pi, size = 5),
})
.with_columns([
(pl.col("r") * pl.col("θ").cos() + p).alias("x0"),
(pl.col("r") * pl.col("θ").sin() + q).alias("x1"),
])
.drop(["r", "θ"])
.to_pandas()
)
# ---- 基準空間に属さない評価用データを作成する ----
np.random.seed(44)
valid_ng = (
pl.DataFrame({
"r": np.random.uniform(low = r_min_ng, high = r_max_ng, size = 5),
"θ": np.random.uniform(low = 0, high = 2 * np.pi, size = 5),
})
.with_columns([
(pl.col("r") * pl.col("θ").cos() + p).alias("x0"),
(pl.col("r") * pl.col("θ").sin() + q).alias("x1"),
])
.drop(["r", "θ"])
.to_pandas()
)
# ---- 学習用データ、基準空間に属する評価用データ、属さない評価用データを返す
return train, valid_ok, valid_ng
前節と同様にまずは生データの分布を可視化します。
基準空間が円周上に分布しており、外れ値が円の中心にあるデータセットです。
データセットを作成する
# ---- データセットを作成する ----
train, valid_ok, valid_ng = make_dataset_circle_2d()
生データの分布をプロットする
# ---- 生データの分布をプロットする ----
# パレット数
row_count = 2
column_count = 2
# Figure
fig = plt.figure(figsize = (6 * row_count + 2, 5 * column_count + 1))# (横, 縦)
# カラーマップ
cmap = plt.get_cmap("tab10")
# x0のプロット
ax_x0 = fig.add_subplot(row_count, column_count, 1)
sns.histplot(data = train, x = "x0", color = cmap(0), ax = ax_x0)
sns.histplot(data = valid_ok, x = "x0", color = cmap(1), ax = ax_x0)
sns.histplot(data = valid_ng, x = "x0", color = cmap(2), ax = ax_x0)
# x1のプロット
ax_x1 = fig.add_subplot(row_count, column_count, 2)
sns.histplot(data = train, x = "x1", color = cmap(0), ax = ax_x1)
sns.histplot(data = valid_ok, x = "x1", color = cmap(1), ax = ax_x1)
sns.histplot(data = valid_ng, x = "x1", color = cmap(2), ax = ax_x1)
# x0 と x1 の散布図
ax_scatter = fig.add_subplot(row_count, column_count, 3)
sns.scatterplot(data = train, x = "x0", y = "x1", ax = ax_scatter, color = cmap(0), label = "Train data")
sns.scatterplot(data = valid_ok, x = "x0", y = "x1", ax = ax_scatter, color = cmap(1), label = "Validation data in base space")
sns.scatterplot(data = valid_ng, x = "x0", y = "x1", ax = ax_scatter, color = cmap(2), label = "Validation data out of base space")
plt.setp(ax_scatter, title = "Raw data", xlabel = "Feature x0", ylabel = "Feature x1")
ax_scatter.legend(bbox_to_anchor=(0, -0.1), loc='upper left', borderaxespad=0, fontsize=18)
plt.suptitle("Raw data distribution")
plt.tight_layout()
plt.show()
MT法で予測できるか確かめてみましょう。
MT法による分類
# ---- MT法のモデルを学習させる ----
model = MahalanobisTaguchiMethod(threshold = 4).fit(X = train)
# ---- 各データのマハラノビス距離を計算する ----
md_train = model.mahalanobis_distance(train)
md_valid_ok = model.mahalanobis_distance(valid_ok)
md_valid_ng = model.mahalanobis_distance(valid_ng)
# ---- 特徴量のヒストグラムと、生データとマハラノビス距離の散布図をプロットする ----
# パレット数
row_count = 2
column_count = 2
# Figure
fig = plt.figure(figsize = (6 * row_count + 2, 5 * column_count + 1))# (横, 縦)
# カラーマップ
cmap = plt.get_cmap("tab10")
# x0のプロット
ax_x0 = fig.add_subplot(row_count, column_count, 1)
sns.histplot(data = train, x = "x0", color = cmap(0), ax = ax_x0)
sns.histplot(data = valid_ok, x = "x0", color = cmap(1), ax = ax_x0)
sns.histplot(data = valid_ng, x = "x0", color = cmap(2), ax = ax_x0)
# x1のプロット
ax_x1 = fig.add_subplot(row_count, column_count, 2)
sns.histplot(data = train, x = "x1", color = cmap(0), ax = ax_x1)
sns.histplot(data = valid_ok, x = "x1", color = cmap(1), ax = ax_x1)
sns.histplot(data = valid_ng, x = "x1", color = cmap(2), ax = ax_x1)
# x0 とマハラノビス距離の散布図
ax_x0_md = fig.add_subplot(row_count, column_count, 3)
sns.scatterplot(x = train["x0"], y = md_train, color = cmap(0), ax = ax_x0_md)
sns.scatterplot(x = valid_ok["x0"], y = md_valid_ok, color = cmap(1), ax = ax_x0_md)
sns.scatterplot(x = valid_ng["x0"], y = md_valid_ng, color = cmap(2), ax = ax_x0_md)
plt.setp(ax_x0_md, yticks = [0, 4], ylabel = "Mahalanobis Distance")
# x1 とマハラノビス距離の散布図
ax_x1_md = fig.add_subplot(row_count, column_count, 4)
sns.scatterplot(x = train["x1"], y = md_train, color = cmap(0), ax = ax_x1_md, label = "Train data")
sns.scatterplot(x = valid_ok["x1"], y = md_valid_ok, color = cmap(1), ax = ax_x1_md, label = "Validation data in base space")
sns.scatterplot(x = valid_ng["x1"], y = md_valid_ng, color = cmap(2), ax = ax_x1_md, label = "Validation data out of base space")
plt.setp(ax_x1_md, yticks = [0, 4], ylabel = "Mahalanobis Distance")
ax_x1_md.legend(bbox_to_anchor=(0, -0.1), loc='upper left', borderaxespad=0, fontsize=18)
plt.suptitle("Compare Raw data distribution and Mahalanobis distance")
plt.tight_layout()
plt.show()

外れ値のデータの方がマハラノビス距離が小さくなってしまいました。
この理由は外れ値の方が学習用データの平均値に近い位置に分布していたからです。
3. 円形に分布しているデータをMT法で処理できるように変換する
MT法で処理できるように前節のデータを変換します。
前節のデータをMT法で分類できるようにする上手い処理の関数
# ---- 円形に分布している2次元データを円の中心を基準とした曲座標系に変換する ----
def to_relative_polar_coordinates(df_pandas, center_x0, center_x1):
df = (
# ---- 処理しやすいPolars dataFrameに戻す ----
pl.from_pandas(df_pandas)
# ---- 中心化 ----
.with_columns([
(pl.col("x0") - center_x0).alias("x0_centering"),
(pl.col("x1") - center_x1).alias("x1_centering"),
])
# ---- 中心からの距離 ----
.with_columns(
(pl.col("x0_centering").pow(2) + pl.col("x1_centering").pow(2)).sqrt().alias("r")
)
# ---- 単位円 ----
.with_columns([
(pl.col("x0_centering") / pl.col("r")).alias("x0_unit"),
(pl.col("x1_centering") / pl.col("r")).alias("x1_unit"),
])
# ---- 三角関数の逆関数 ----
.with_columns([
pl.col("x0_unit").arccos().alias("θcos"),
pl.col("x1_unit").arcsin().alias("θsin"),
])
# ---- 位相 ----
.with_columns(
pl
# 第1象限
.when( (pl.col("x0_unit") >= 0) & (pl.col("x1_unit") >= 0) ).then( pl.col("θcos") )
# 第2象限
.when( (pl.col("x0_unit") < 0) & (pl.col("x1_unit") >= 0) ).then( pl.col("θsin") + np.pi / 2 )
# 第3象限
.when( (pl.col("x0_unit") < 0) & (pl.col("x1_unit") < 0) ).then( pl.col("θsin") + 3 * np.pi / 2 )
# 第4象限
.otherwise(pl.col("θcos") + 3 * np.pi / 2)
.alias("θ")
)
# ---- 不要な列の削除
.drop([
"x0", "x1",
"x0_centering", "x1_centering",
"x0_unit", "x1_unit",
"θcos", "θsin",
])
# ---- Pnadas DataFrameへ変換する
.to_pandas()
)
return df
上手い処理を実行する
# 曲座標に変換するためのパラメータ
center_x0 = np.mean(train["x0"], axis = 0)
center_x1 = np.mean(train["x1"], axis = 0)
train_polar = to_relative_polar_coordinates(train, center_x0, center_x1)
valid_ok_polar = to_relative_polar_coordinates(valid_ok, center_x0, center_x1)
valid_ng_polar = to_relative_polar_coordinates(valid_ng, center_x0, center_x1)
変換したデータの分布をプロットします。
MT法を使わずとも 動径成分 r だけで分離できます。
生データの分布をプロットする
# ---- 生データの分布をプロットする ----
# パレット数
row_count = 2
column_count = 2
# Figure
fig = plt.figure(figsize = (6 * row_count + 2, 5 * column_count + 1))# (横, 縦)
# カラーマップ
cmap = plt.get_cmap("tab10")
# x0のプロット
ax_x0 = fig.add_subplot(row_count, column_count, 1)
sns.histplot(data = train_polar, x = "r", color = cmap(0), ax = ax_x0)
sns.histplot(data = valid_ok_polar, x = "r", color = cmap(1), ax = ax_x0)
sns.histplot(data = valid_ng_polar, x = "r", color = cmap(2), ax = ax_x0)
# x1のプロット
ax_x1 = fig.add_subplot(row_count, column_count, 2)
sns.histplot(data = train_polar, x = "θ", color = cmap(0), ax = ax_x1)
sns.histplot(data = valid_ok_polar, x = "θ", color = cmap(1), ax = ax_x1)
sns.histplot(data = valid_ng_polar, x = "θ", color = cmap(2), ax = ax_x1)
# r と θ の散布図
ax_scatter = fig.add_subplot(row_count, column_count, 3)
sns.scatterplot(data = train_polar, x = "r", y = "θ", ax = ax_scatter, color = cmap(0), label = "Train data")
sns.scatterplot(data = valid_ok_polar, x = "r", y = "θ", ax = ax_scatter, color = cmap(1), label = "Validation data in base space")
sns.scatterplot(data = valid_ng_polar, x = "r", y = "θ", ax = ax_scatter, color = cmap(2), label = "Validation data out of base space")
plt.setp(ax_scatter, title = "Raw data", xlabel = "Feature r", ylabel = "Feature θ")
ax_scatter.legend(bbox_to_anchor=(0, -0.1), loc='upper left', borderaxespad=0, fontsize=18)
plt.suptitle("Modified data distribution")
plt.tight_layout()
plt.show()

MT法の結果を確認します。
MT法を試す
# ---- MT法のモデルを学習させる ----
model = MahalanobisTaguchiMethod(threshold = 4).fit(X = train_polar)
# ---- 各データのマハラノビス距離を計算する ----
md_train = model.mahalanobis_distance(train_polar)
md_valid_ok = model.mahalanobis_distance(valid_ok_polar)
md_valid_ng = model.mahalanobis_distance(valid_ng_polar)
# ---- 特徴量のヒストグラムと、生データとマハラノビス距離の散布図をプロットする ----
# パレット数
row_count = 2
column_count = 2
# Figure
fig = plt.figure(figsize = (6 * row_count + 2, 5 * column_count + 1))# (横, 縦)
# カラーマップ
cmap = plt.get_cmap("tab10")
# x0のプロット
ax_x0 = fig.add_subplot(row_count, column_count, 1)
sns.histplot(data = train_polar, x = "r", color = cmap(0), ax = ax_x0)
sns.histplot(data = valid_ok_polar, x = "r", color = cmap(1), ax = ax_x0)
sns.histplot(data = valid_ng_polar, x = "r", color = cmap(2), ax = ax_x0)
# x1のプロット
ax_x1 = fig.add_subplot(row_count, column_count, 2)
sns.histplot(data = train_polar, x = "θ", color = cmap(0), ax = ax_x1)
sns.histplot(data = valid_ok_polar, x = "θ", color = cmap(1), ax = ax_x1)
sns.histplot(data = valid_ng_polar, x = "θ", color = cmap(2), ax = ax_x1)
# r とマハラノビス距離の散布図
ax_r_md = fig.add_subplot(row_count, column_count, 3)
sns.scatterplot(x = train_polar["r"], y = md_train, color = cmap(0), ax = ax_r_md)
sns.scatterplot(x = valid_ok_polar["r"], y = md_valid_ok, color = cmap(1), ax = ax_r_md)
sns.scatterplot(x = valid_ng_polar["r"], y = md_valid_ng, color = cmap(2), ax = ax_r_md)
plt.setp(ax_r_md, yticks = [0, 4], ylabel = "Mahalanobis Distance")
# x1 とマハラノビス距離の散布図
ax_θ_md = fig.add_subplot(row_count, column_count, 4)
sns.scatterplot(x = train_polar["θ"], y = md_train, color = cmap(0), ax = ax_θ_md, label = "Train data")
sns.scatterplot(x = valid_ok_polar["θ"], y = md_valid_ok, color = cmap(1), ax = ax_θ_md, label = "Validation data in base space")
sns.scatterplot(x = valid_ng_polar["θ"], y = md_valid_ng, color = cmap(2), ax = ax_θ_md, label = "Validation data out of base space")
plt.setp(ax_θ_md, yticks = [0, 4], ylabel = "Mahalanobis Distance")
ax_θ_md.legend(bbox_to_anchor=(0, -0.1), loc='upper left', borderaxespad=0, fontsize=18)
plt.suptitle("Compare Modified data distribution and Mahalanobis distance")
plt.tight_layout()
plt.show()

無事に分離することができました。
終わりに
MT法が上手くデータセットとそうでないものをPythonコードで試してみました。
線形な相関関係から外れたデータに対してMT法が上手くいくことが分かりました。
上手くいかないものでも変数変換次第では上手くいくことがあります。
Discussion