🦆

6.1 ABテストの効果検証 - 第6章ベイズ推論の業務活用事例

2025/11/01に公開

はじめに

Pythonでスラスラわかるベイズ推論「超」入門(赤石雅典 (著), 須山敦志 (監修))の6.1節のPyMCコードをNumPyroで書き直しました。
業務で使用することが多いABテストをベイズ推論します。
シンプルながら奥が深い分析です。

フォルダ構造とユーティリティ関数、ライブラリimport

リンク集の記事にフォルダ構造とユーティリティ関数、ライブラリimportを掲載しました。
準備としてそちらのページをご覧ください。

6.1 ABテストの効果検証

6.1.1 問題設定

参考書籍の問題文を引用します。

鈴木さんと山田さんは、それぞれ自分の担当のWebページを持っており、担当頁に改善を加えました。
そして、回前後のページBと従来のページAをランダムに提示するABテストを実施し、効果検証をしました。
その結果が表6.1.1のとおりであった場合、2人それぞれの改善に効果があったかどうかを判断したいということがビジネス上の課題と考えてください。

_	_	鈴木さん	山田さん
従来のページA	表示数	40	1,200
_	クリック数	2	60
_	クリック率	5%	5%
改善後のページB	表示数	25	1,500
_	クリック数	2	110
_	クリック率	8%	6.88%

6.1.2 確率モデル定義(鈴木さんの場合)

表示数とクリック数の結果を集計したデータで分析する場合を考えます。
表示回数 $n$ 回のうちクリック数が $y$ 回の場合のモデルを作成します。

まず、あるユーザーがクリックした/しないの結果が他のユーザーの行動に一切影響しない、かつクリック率は一定であると仮定します。
クリック数 $y$ は二項分布に従うと仮定するのが自然です。

y \sim Bi(y|p, n)

次に、クリック率の推論精度を高める情報はありません。
そのため、確率 $p$ の事前分布は一様分布 $[0,1]$ と仮定するのが無難です。

p \sim Uniform(0, 1)

ここまでの結果を条件付確率の比例式に当てはめます。

\begin{aligned} P(H = p|D = (y, n)) \propto& P(D = (y, n),H = p)\\ =& P(y, (n, p))\\ =& P(y|(n, p)) \times P(n, p)\\ =& P(y|(n, p)) \times P(p) \times P(n)\\ \propto& P(y|(n, p)) \times P(p)\\ =& Bi(y|p, n) \times Uniform(0, 1) \end{aligned}

Webページの改善の効果を調べるので、改善前後のクリック率の差(ポイント)の事後分布で評価します。

p_{B} - p_{A}

ここまでの仮定を、後ろの方から記述します。

def model_ab_test(n_a, y_a, n_b, y_b):
    '''
        6.1節のABテストのモデル
    '''
    # 確率 $p$ の事前分布は一様分布 $[0,1]$ と仮定するのが無難です。
    p_a = numpyro.sample("p_a", dist.Uniform(low = 0, high = 1))
    p_b = numpyro.sample("p_b", dist.Uniform(low = 0, high = 1))
    # クリック数 $y$ は二項分布に従うと仮定するのが自然です
    c_a = numpyro.sample("c_a", dist.Binomial(total_count = n_a, probs = p_a), obs = y_a)
    c_b = numpyro.sample("c_b", dist.Binomial(total_count = n_b, probs = p_b), obs = y_b)
    # 改善前後のクリック率の差(ポイント)の事後分布で評価します
    Δp = numpyro.deterministic("Δp", p_b - p_a)

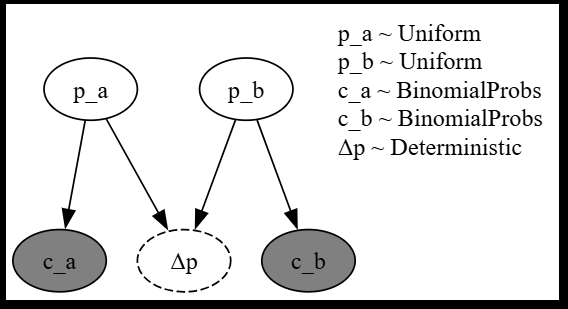
作成したモデルをプロットします。
モデル化するとパラメータの関係性が分かります。

model_args = {
    "n_a": 40,
    "y_a": 2,
    "n_b": 25,
    "y_b": 2,
}
try_render_model(model_ab_test, render_name = "ABテストのモデル", **model_args)

6.1.3 サンプリングと結果分析

データを用意してモデルを作成したら後はユーティリティ関数に渡すだけです。

model_args = {
    "n_a": 40,
    "y_a": 2,
    "n_b": 25,
    "y_b": 2,
}
idata = run_mcmc(
    model_ab_test,
    num_chains = 4,
    num_warmup = 1000,
    num_samples = 1000,
    thinning = 1,
    seed = 42,
    target_accept_prob = 0.99,
    log_likelihood = False,
    **model_args
)

まずはサンプリングが上手くいったか確認します。

az.plot_trace(idata, compact = False, var_names = ["p_a", "p_b", "Δp"])
plt.tight_layout()

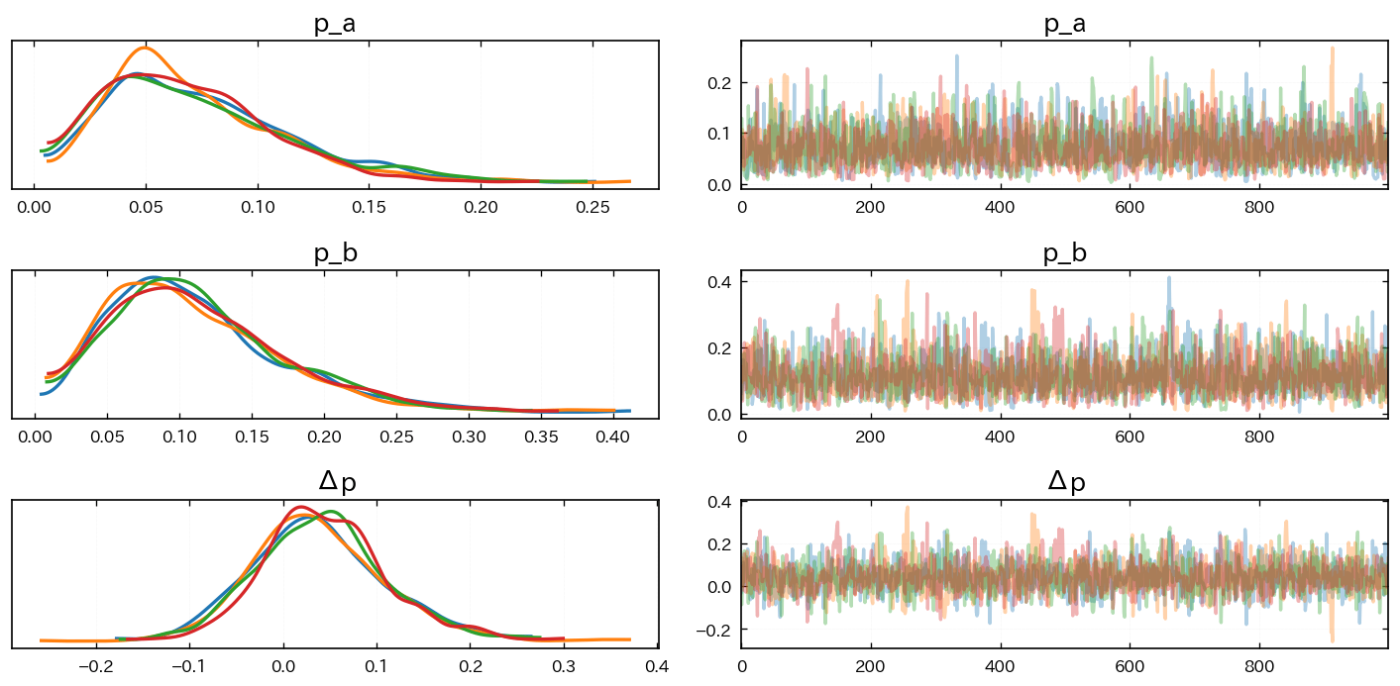
知りたかったクリック率の差(ポイント)の事後分布をプロットします。

ax = az.plot_posterior(idata, var_names=["Δp"])
xx, yy = ax.get_lines()[0].get_data()
ax.fill_between(xx[xx<0], yy[xx<0]);
plt.suptitle("鈴木さんのWebページのクリック率改善度合い")

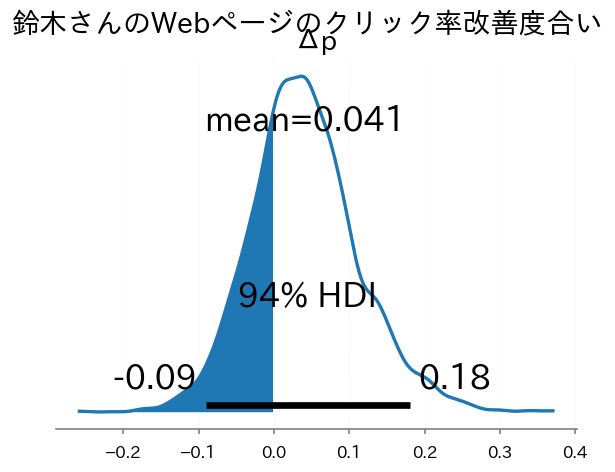
改善前のWebページの方がクリック率が高い確率を計算します。
$28 \%$ の確率で改善前の方がクリック率が高いという結果が出ました。
改善効果がある確率が7割というのはやや信頼性が足りません。

# サンプリング結果から　delta_probの値を抽出
delta_prob_s = idata['posterior'].data_vars['Δp']
delta_prob_s_values = delta_prob_s.values.reshape(-1)

# delta_probの値がマイナスであった件数
n1_s = (delta_prob_s_values < 0).sum()

# 全体サンプル数
n_s = len(delta_prob_s_values)

# 比率計算
n1_rate_s = n1_s/n_s
print(f'鈴木さんケース　画面Aの方がクリック率が高い確率: {n1_rate_s*100:.02f}%')

6.1.4 山田さんの場合

モデルに渡すデータを変えてもう一度サンプリングを行います。

model_args = {
    "n_a": 1200,
    "y_a": 60,
    "n_b": 1500,
    "y_b": 110,
}
idata = run_mcmc(
    model_ab_test,
    num_chains = 4,
    num_warmup = 1000,
    num_samples = 1000,
    thinning = 1,
    seed = 42,
    target_accept_prob = 0.99,
    log_likelihood = False,
    **model_args
)

まずはサンプリングが上手くいったか確認します。

az.plot_trace(idata, compact = False, var_names = ["p_a", "p_b", "Δp"])
plt.tight_layout()

知りたかったクリック率の差(ポイント)の事後分布をプロットします。

ax = az.plot_posterior(idata, var_names=["Δp"])
xx, yy = ax.get_lines()[0].get_data()
ax.fill_between(xx[xx<0], yy[xx<0]);
plt.suptitle("山田さんのWebページのクリック率改善度合い")

改善前のWebページの方がクリック率が高い確率を計算します。
$0.75 \%$ の確率で改善前の方がクリック率が高いという結果が出ました。
改善効果がある確率が99%というのはとても良いと考えられます。

# サンプリング結果から　delta_probの値を抽出
delta_prob_s = idata['posterior'].data_vars['Δp']
delta_prob_s_values = delta_prob_s.values.reshape(-1)

# delta_probの値がマイナスであった件数
n1_s = (delta_prob_s_values < 0).sum()

# 全体サンプル数
n_s = len(delta_prob_s_values)

# 比率計算
n1_rate_s = n1_s/n_s
print(f'山田さんケース　画面Aの方がクリック率が高い確率: {n1_rate_s*100:.02f}%')

6.1.5 確率モデルを直接使った別解

省略

終わりに

業務で使用することが多いABテストをベイズ推論しました。
シンプルながら奥が深い分析です。
書籍でも言及されていましたが、ベイズ推論は事後分布を直接扱えるので直感的な分析が行えます。