🦆

5.1 データ分布のベイズ推論 - 第5章ベイズ推論プログラミング

2025/11/01に公開

はじめに

Pythonでスラスラわかるベイズ推論「超」入門(赤石雅典 (著), 須山敦志 (監修))の5.1節のPyMCコードをNumPyroで書き直しました。
アイリス・データセットを使ってSetosaのがく片の長さsepal_lengthの分布を例に正規分布のベイズ推論を行います。
ここから条件付確率 $P(H|D)=P(D,H)/P(D)$ の比例式 $P(H|D) \propto P(D,H)$ と確率モデルとの関係が分かりにくくなります。

フォルダ構造とユーティリティ関数、ライブラリimport

リンク集の記事にフォルダ構造とユーティリティ関数、ライブラリimportを掲載しました。
準備としてそちらのページをご覧ください。

5.1 データ分布のベイズ推論

5.1.1 問題設定

setosaのsepal_lengthのデータ分布が正規分布に従うと仮定して、sepal_lengthの分布の形を調べます。

5.1.2 データ準備

seabornのirisデータセットを読み込みます。
setosaの萼片（がくへん）の長さsepal_lengthを抽出します。
sepal_lengthの分布に興味があるため目的変数の $y$ とします。
sepal_lengthのヒストグラムをプロットすると正規分布の釣り鐘型に近い分布がプロットされました。
正規分布で近似してよさそうです。

# データセットを読み込む
df = sns.load_dataset("iris")

# setosa を抽出する
df_setosa = df.query('species == "setosa"')

# ヒストグラムを描画
bins = np.arange(4.0, 6.2, 0.2)
sns.histplot(data = df_setosa, x = "sepal_length", bins = bins, kde = True)
plt.xticks(bins);

# NumPy変数の1次元配列に変換
Y = jnp.array(df_setosa['sepal_length'].values, dtype = float)

# 統計情報の確認
print(df_setosa['sepal_length'].describe())

# 値の確認
print(Y)

5.1.3 確率モデル定義

確率モデルをプログラミングするために、全勝と同様に数式を使って状況を整理します。

まず、ヒストグラムより $N$ 個の sepal_length $\{ y_{i} \}$ は正規分布に従うと仮定します。
正規分布は平均 $\mu$ と標準偏差 $\sigma$ で確率分布の形状が決まります。
本節のベイズ推論は平均 $\mu$ と標準偏差 $\sigma$ を求める問題になります。

y_{i} \sim N(\mu, \sigma^2)

次に、正規分布のパラメータの推論精度を高める情報はありません。
広めの事前分布を与えておきましょう。
平均 $\mu$ は平均0, 標準偏差10の正規分布に従うと仮定します。
標準偏差 $\sigma$ は標準偏差10の半正規分布に従うと仮定します。
さらに、平均 $\mu$ と標準偏差 $\sigma$ は独立であると仮定します。

\begin{aligned} \mu \sim& N(0,10^2)\\ \sigma \sim& HN(0,10^2)\\ P(\mu, \sigma) =& P(\mu) \times P(\sigma) \end{aligned}

ここまでの結果を条件付確率 $P(H|D)=P(D,H)/P(D)$ の比例式 $P(H|D) \propto P(D,H)$ に当てはめます。

\begin{aligned} P(H = (\mu, \sigma)|D = y) \propto& P(D = y,H = (\mu, \sigma))\\ =& P(D = y|H = (\mu, \sigma)) \times P(\mu, \sigma)\\ =& P(D = y|H = (\mu, \sigma)) \times P(\mu) \times P(\sigma)\\ =& N(\mu, \sigma^2) \times N(0,10^2) \times HN(0,10^2) \end{aligned}

PyMCやNumPyroのプログラミングは、右辺の最後の式を後ろから記述します。

def model_normal(N, Y = None):
    '''
        5.1節のSetosaのがく片長さの確率分布モデル
    '''
    # 標準偏差 $\sigma$ は標準偏差10の半正規分布に従うと仮定します
    sigma = numpyro.sample("sigma", dist.HalfNormal(scale = 10))
    # 平均 $\mu$ は平均0, 標準偏差10の正規分布に従うと仮定します
    mu = numpyro.sample("mu", dist.Normal(loc = 0, scale = 10))
    # ```sepal_length```は正規分布に従うと仮定します
    # ベクトル化(学習用データを確率変数に割り当てるためのNumPyroのお作法)
    with numpyro.plate("N", N):
        numpyro.sample("Y", dist.Normal(loc = mu, scale = sigma), obs = Y)

model_args = {
    "N": len(Y),
    "Y": Y
}
try_render_model(model_normal, render_name = "Setosaｎがく片の長さの正規分布近似", **model_args)

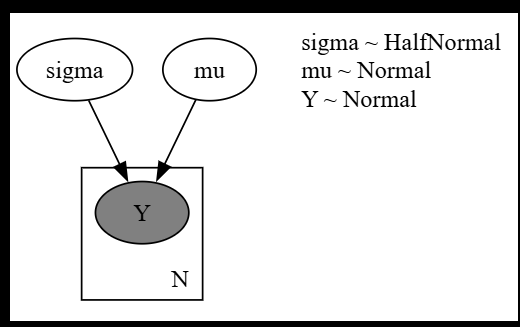
5.1.4 サンプリング

データを用意してモデルを作成したら後はユーティリティ関数に渡すだけです。

model_args = {
    "N": len(Y),
    "Y": Y
}
idata = run_mcmc(
    model_normal,
    num_chains = 4,
    num_warmup = 1000,
    num_samples = 1000,
    thinning = 1,
    seed = 42,
    target_accept_prob = 0.8,
    log_likelihood = False,
    **model_args
)

5.1.5 結果分析

ここからは書籍のコードとほぼ同じです。

まずはサンプリングが上手くいったか確認します。

az.plot_trace(idata, compact = False)
plt.tight_layout()

正規分布のパラメータの事後分布をプロットします。
正規分布の平均値 $\mu$ に注目すると事後分布の平均値が5でヒストグラムの結果通りです。

ax = az.plot_posterior(idata)
plt.suptitle("Setosaのがく片長さの確率分布の形状")
plt.tight_layout()
plt.show()

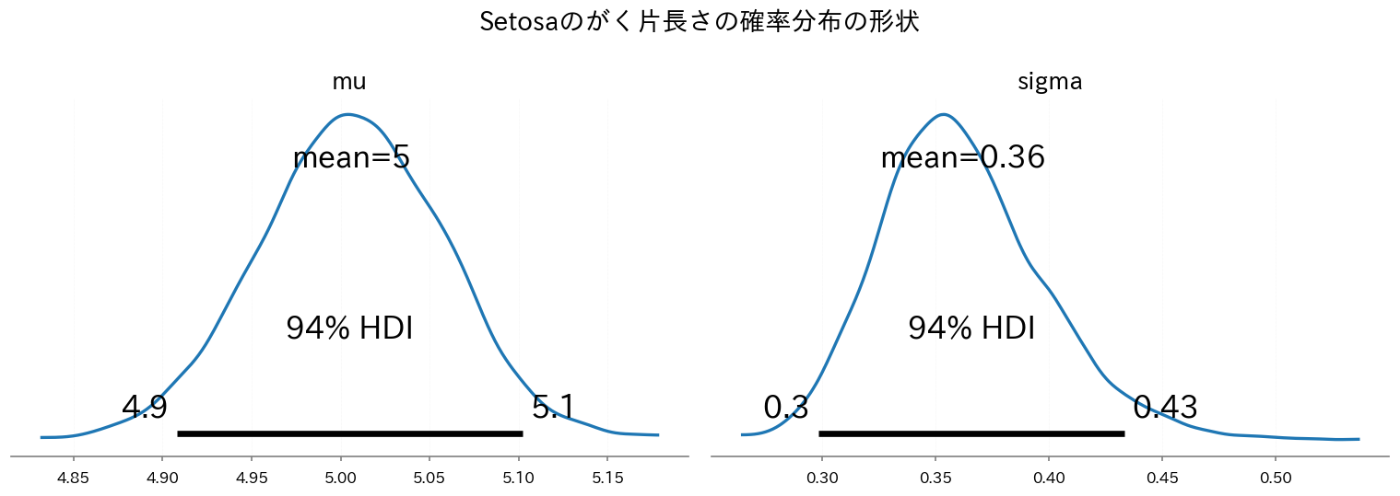
集計用のデータも確認します。

summary = az.summary(idata)
display(summary)

summaryはpandas DataFrameのため次のコードのような面白い抽出ができます。

print(f"mu={summary.loc["mu", "mean"]}, sigma={summary.loc["sigma", "mean"]}")

5.1.6 ヒストグラムと正規分布関数の重ね書き

書籍のコードから変数名を変えています。
ベイズ推論で計算した正規分布をヒストグラムに重ねるとほぼ一致したので、良い推論ができたと判断します。

def norm(x, mu, sigma):
    """
    正規分布のラインプロットの確率密度関数の値を計算する
    """
    y = (x-mu)/sigma
    a = np.exp(-(y**2)/2)
    b = np.sqrt(2*np.pi)*sigma
    return a/b

# 変更点
x_min = Y.min()
x_max = Y.max()
x_list = np.arange(x_min, x_max, 0.01)
y_list = norm(x_list, summary.loc["mu", "mean"], summary.loc["sigma", "mean"])

delta = 0.2
bins=np.arange(4.0, 6.0, delta)
fig, ax = plt.subplots()
sns.histplot(df_setosa, ax=ax, x='sepal_length',
    bins=bins, kde=True, stat='probability')
ax.get_lines()[0].set_label('KDE曲線')
ax.set_xticks(bins)
ax.plot(x_list, y_list*delta, c='r', label='ベイズ推論結果')
ax.set_title('ベイズ推論結果とKDE曲線の比較')
plt.legend();

5.1.7 少ないサンプル数でのベイズ推論

省略

終わりに

正規分布の例を使ってベイズ推論を行いました。
数式の準備以外は前章のくじ引きと同じ流れです。