はじめに
k平均法は理論の分かりやすさ・実装の簡単さから、分類問題の手法として最初に候補に挙がるものだと思います。しかし、2次元空間では円、3次元では球体、高次では超球で括ることができるデータでないと分類が上手くいかない場合があります。
今回の記事では、そんなちょっとひねくれた形状を分類できるスペクトラルクラスタリングを手計算で解きます。
機械学習で、k平均法の次のクラスタリング手法を勉強中の方のお役に立てれば幸いです。
例題
下図のデータをスペクトラルクラスタリングで分類します。明らかに2つのコの字で分類できますが、k平均法では上手くいかない典型です。
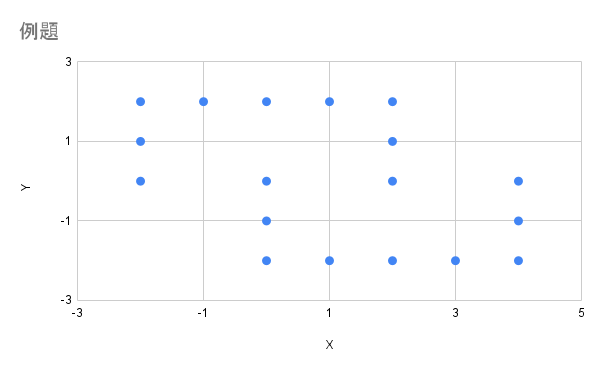
各データ点の座標で計画行列を作ると下記になります。手計算で18点はとてもつらいですが頑張ります。
X=
\begin{pmatrix}
-2 & 0 \\
-2 & 1 \\
-2 & 2 \\
-1 & 2 \\
0 & 2 \\
1 & 2 \\
2 & 2 \\
2 & 1 \\
2 & 0 \\
0 & 0 \\
0 & -1 \\
0 & -2 \\
1 & -2 \\
2 & -2 \\
3 & -2 \\
4 & -2 \\
4 & -1 \\
4 & 0 \\
\end{pmatrix}
特徴量の抽出
スペクトラルクラスタリングは、データ点同士の関係を特徴量として、その固有ベクトルでk平均法を解くことで、複雑な形状でも分類できるようになります。今回の例題ではk近傍法を特徴量として解きたいと思います。
データ点同士の距離
スペクトラルクラスタリングのk近傍法は、データ点同士の距離が近いペアに重みを与えます。ということで頑張って18点の距離を計算します。距離が近い順を知りたいので根号計算のいらない二乗で大丈夫です。
Metric^2=
\begin{pmatrix}
0 & 1 & 4 & 5 & 8 & 13 & 20 & 17 & 16 & 4 & 5 & 8 & 13 & 20 & 29 & 40 & 37 & 36\\
1 & 0 & 1 & 2 & 5 & 10 & 17 & 16 & 17 & 5 & 8 & 13 & 18 & 25 & 34 & 45 & 40 & 37\\
4 & 1 & 0 & 1 & 4 & 9 & 16 & 17 & 20 & 8 & 13 & 20 & 25 & 32 & 41 & 52 & 45 & 40\\
5 & 2 & 1 & 0 & 1 & 4 & 9 & 10 & 13 & 5 & 10 & 17 & 20 & 25 & 32 & 41 & 34 & 29\\
8 & 5 & 4 & 1 & 0 & 1 & 4 & 5 & 8 & 4 & 9 & 16 & 17 & 20 & 25 & 32 & 25 & 20\\
13 & 10 & 9 & 4 & 1 & 0 & 1 & 2 & 5 & 5 & 10 & 17 & 16 & 17 & 20 & 25 & 18 & 13\\
20 & 17 & 16 & 9 & 4 & 1 & 0 & 1 & 4 & 8 & 13 & 20 & 17 & 16 & 17 & 20 & 13 & 8\\
17 & 16 & 17 & 10 & 5 & 2 & 1 & 0 & 1 & 5 & 8 & 13 & 10 & 9 & 10 & 13 & 8 & 5\\
16 & 17 & 20 & 13 & 8 & 5 & 4 & 1 & 0 & 4 & 5 & 8 & 5 & 4 & 5 & 8 & 5 & 4\\
4 & 5 & 8 & 5 & 4 & 5 & 8 & 5 & 4 & 0 & 1 & 4 & 5 & 8 & 13 & 20 & 17 & 16\\
5 & 8 & 13 & 10 & 9 & 10 & 13 & 8 & 5 & 1 & 0 & 1 & 2 & 5 & 10 & 17 & 16 & 17\\
8 & 13 & 20 & 17 & 16 & 17 & 20 & 13 & 8 & 4 & 1 & 0 & 1 & 4 & 9 & 16 & 17 & 20\\
13 & 18 & 25 & 20 & 17 & 16 & 17 & 10 & 5 & 5 & 2 & 1 & 0 & 1 & 4 & 9 & 10 & 13\\
20 & 25 & 32 & 25 & 20 & 17 & 16 & 9 & 4 & 8 & 5 & 4 & 1 & 0 & 1 & 4 & 5 & 8\\
29 & 34 & 41 & 32 & 25 & 20 & 17 & 10 & 5 & 13 & 10 & 9 & 4 & 1 & 0 & 1 & 2 & 5\\
40 & 45 & 52 & 41 & 32 & 25 & 20 & 13 & 8 & 20 & 17 & 16 & 9 & 4 & 1 & 0 & 1 & 4\\
37 & 40 & 45 & 34 & 25 & 18 & 13 & 8 & 5 & 17 & 16 & 17 & 10 & 5 & 2 & 1 & 0 & 1\\
36 & 37 & 40 & 29 & 20 & 13 & 8 & 5 & 4 & 16 & 17 & 20 & 13 & 8 & 5 & 4 & 1 & 0\\
\end{pmatrix}
各データ点からの距離の昇順
各データ点を基準とする距離の昇順を計算します。
Rank=
\begin{pmatrix}
1 & 2 & 3 & 5 & 7 & 9 & 13 & 12 & 11 & 3 & 5 & 7 & 9 & 13 & 15 & 18 & 17 & 16\\
2 & 1 & 2 & 4 & 5 & 8 & 11 & 10 & 11 & 5 & 7 & 9 & 13 & 14 & 15 & 18 & 17 & 16\\
4 & 2 & 1 & 2 & 4 & 7 & 9 & 10 & 11 & 6 & 8 & 11 & 13 & 14 & 16 & 18 & 17 & 15\\
6 & 4 & 2 & 1 & 2 & 5 & 8 & 9 & 11 & 6 & 9 & 12 & 13 & 14 & 16 & 18 & 17 & 15\\
9 & 7 & 4 & 2 & 1 & 2 & 4 & 7 & 9 & 4 & 11 & 12 & 13 & 14 & 16 & 18 & 16 & 14\\
11 & 9 & 8 & 5 & 2 & 1 & 2 & 4 & 6 & 6 & 9 & 14 & 13 & 14 & 17 & 18 & 16 & 11\\
16 & 13 & 11 & 8 & 4 & 2 & 1 & 2 & 4 & 6 & 9 & 16 & 13 & 11 & 13 & 16 & 9 & 6\\
17 & 16 & 17 & 11 & 5 & 4 & 2 & 1 & 2 & 5 & 8 & 14 & 11 & 10 & 11 & 14 & 8 & 5\\
16 & 17 & 18 & 15 & 12 & 7 & 3 & 2 & 1 & 3 & 7 & 12 & 7 & 3 & 7 & 12 & 7 & 3\\
3 & 7 & 12 & 7 & 3 & 7 & 12 & 7 & 3 & 1 & 2 & 3 & 7 & 12 & 15 & 18 & 17 & 16\\
5 & 8 & 14 & 11 & 10 & 11 & 14 & 8 & 5 & 2 & 1 & 2 & 4 & 5 & 11 & 17 & 16 & 17\\
6 & 9 & 16 & 13 & 11 & 13 & 16 & 9 & 6 & 4 & 2 & 1 & 2 & 4 & 8 & 11 & 13 & 16\\
11 & 16 & 18 & 17 & 14 & 13 & 14 & 9 & 6 & 6 & 4 & 2 & 1 & 2 & 5 & 8 & 9 & 11\\
14 & 16 & 18 & 16 & 14 & 13 & 12 & 11 & 4 & 9 & 7 & 4 & 2 & 1 & 2 & 4 & 7 & 9\\
15 & 17 & 18 & 16 & 14 & 13 & 12 & 9 & 6 & 11 & 9 & 8 & 5 & 2 & 1 & 2 & 4 & 6\\
15 & 17 & 18 & 16 & 14 & 13 & 11 & 8 & 6 & 11 & 10 & 9 & 7 & 4 & 2 & 1 & 2 & 4\\
16 & 17 & 18 & 15 & 14 & 13 & 9 & 7 & 5 & 11 & 10 & 11 & 8 & 5 & 4 & 2 & 1 & 2\\
16 & 17 & 18 & 15 & 13 & 9 & 7 & 5 & 3 & 11 & 12 & 13 & 9 & 7 & 5 & 3 & 2 & 1\\
\end{pmatrix}
特徴量(各データ点からの距離の昇順の上位への重みづけ) = 隣接行列
自分以外の各データ点への距離の近い点の上位への重みづけを特徴量とします。この特徴量の行列を隣接行列と呼びます。今回は同率2位までのペアに重みづけをしました。
A=
\begin{pmatrix}
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 1\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\
\end{pmatrix}
重みづけしたペアの一部を線で結ぶと下図になります。基本的には最近傍の1点とのペアを作りますが、同率のデータ点があると多くのペアができます。赤色の線は(-2,0)と(-2,1)とを結ぶ線です。緑色は(-2,2)との、紫色は(2,1)との、黄色は(0,0)との最近傍点とを結ぶ線です。
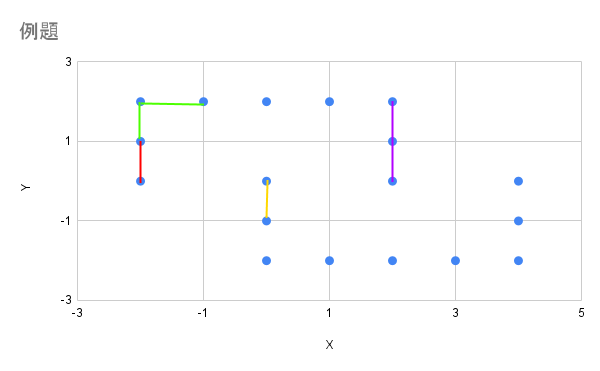
次数行列
前節の隣接行列をよく見ると、9行目の(2,0)と10行目の(0,0)の前後でデータ点がつながっていないことがわかります。目視でつながっていないことが分かる場合はそこで境界線を敷くことも手ですが、実際の例では境界線が見えることはまれでしょう。
そこで、この特徴量の主成分を抽出して機械的に分類できるようにしたいと思います。主成分計算のためのステップとして、下記の次数行列と次節のラプラシアンを経由します。
D_{i,j}=
\begin{cases}
\sum_{k=1}^N a_{i,k} & i=j\\
0 & otherwise\\
\end{cases}
ラプラシアン
定義は簡単ですが、実際に打ってみるとえげつないです。
L = D - A\\
=
\begin{pmatrix}
1 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
-1 & 2 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & -1 & 2 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & -1 & 2 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & -1 & 2 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & -1 & 2 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & -1 & 2 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & -1 & 2 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 2 & -1 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 2 & -1 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 2 & -1 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 2 & -1 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 2 & -1 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 2 & -1 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 2 & -1\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 1\\
\end{pmatrix}
ラプラシアンの固有値は計算しません。
余因子展開を15、16回も行ったら大変なことになりますし、今回の例は固有ベクトルを直接計算できますからね、仕方ないね。
L \vec{x} = \lambda \vec{x}\\
\left(L-\lambda I\right)\vec{x}=\vec{0}\\
\rightarrow \left | L-\lambda I\right | =0\\
特徴量の固有ベクトル(ラプラシアンの固有ベクトル)
9番目までと10番目以降で重みづけが切れているので、2クラス分類したい場合の固有ベクトルは下記になります。
\vec{x}=
\begin{pmatrix}
1 & 0 \\
1 & 0 \\
1 & 0 \\
1 & 0 \\
1 & 0 \\
1 & 0 \\
1 & 0 \\
1 & 0 \\
1 & 0 \\
0 & 1 \\
0 & 1 \\
0 & 1 \\
0 & 1 \\
0 & 1 \\
0 & 1 \\
0 & 1 \\
0 & 1 \\
0 & 1 \\
\end{pmatrix}
ラプラシアンの固有ベクトルをk平均法で解く
固有ベクトル\vec{x}は明らかに(1,0)と(0,1)に凝集しているので、k平均法で2クラス分類できます。
Label(\vec{x})=
\begin{pmatrix}
0 \\
0 \\
0 \\
0 \\
0 \\
0 \\
0 \\
0 \\
0 \\
1 \\
1 \\
1 \\
1 \\
1 \\
1 \\
1 \\
1 \\
1 \\
\end{pmatrix}
2クラス分類の結果
2クラス分類した結果の散布図を下記に示します。見事に2つのコの字で分類できました。
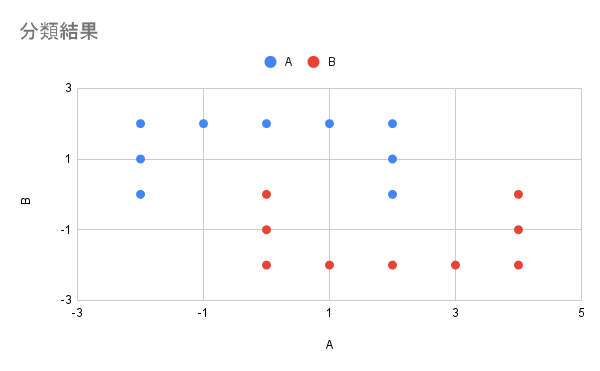
終わりに
計算が大変です。k平均法が手法の一部に組み込まれている時点で戦闘力のインフレを感じます。



Discussion