第4章 はじめてのベイズ推論実習

はじめに

Pythonでスラスラわかる ベイズ推論「超」入門(赤石 雅典 (著), 須山 敦志 (監修))の第4章のPyMCコードをNumPyroで書き直しました。
くじ引きを例にベルヌーイ分布と二項分布のベイズ推論を行います。
この例で数式から書き始めるのは冗長ですが、後の例の練習と信じてお付き合いください。

フォルダ構造とユーティリティ関数、ライブラリimport

リンク集の記事にフォルダ構造とユーティリティ関数、ライブラリimportを掲載しました。
準備としてそちらのページをご覧ください。

1. フォルダ構造とユーティリティ関数
2. ライブラリimport

4.1 問題設定

参考書籍の問題文を引用します。

常に確率が一定で、前回の結果が次回に一切影響しないくじ引きがあります。
ある人がこのくじ引きを5回引いたところ、結果は「当たり、はずれ、はずれ、当たり、はずれ」でした。
1回のくじ引きに当たる確率を $p$ とするとき、この $p$ の値を求めなさい。

4.2 最尤推定

ベイズ推論ではないので省略します。

4.3 ベイズ推論(確率モデル定義)

ベイズ推論の大きな流れは下記の通りです。
参考書籍のPyMCの部分をNumPyroで書き直します。

序数	項目	説明
1	データ準備	通常の機械学習と同じ。 pandas/NumPyなどで実施する。
2	確率モデル定義	確率変数の関係を確率モデル化し、PyMCなどで記述する。
3	サンプリング	サンプリングデータの生成。PyMCのsample関数により実施する。
4	結果分析	主にArviZライブラリを用いて、サンプリング結果を統計的に分析する。

Step 1. データ準備
くじ引きの結果は「試行の結果」であるため、書籍の $X$ ではなく目的変数の $Y$ を使います。
複数回の試行結果を1次元の配列 $Y \equiv (y_{0}, \cdots, y_{4})^{T}$ にデータをまとめる。

Y = jnp.array([1, 0, 0, 1, 0], dtype = int)

Step 2. 確率モデル定義
確率モデルをプログラミングするために、数式を使って状況を整理します。

まず、前回の結果が次回に一切影響しない、かつ確率が一定のくじ引きであると仮定しました。
くじ引きの結果 $y_{i} \ (i = 0, \cdots, 4)$ がベルヌーイ分布に従うと仮定するのが自然です。

$$y \sim Bern(y∣p)$$

次に、くじ引きの確率の推論精度を高める情報はありません。
そのため、確率 $p$ の事前分布は一様分布 $[0,1]$ と仮定するのが無難です。

$$p \sim Uniform(0, 1)$$

ここまでの結果を条件付確率 $P(H|D)=P(D,H)/P(D)$ の比例式 $P(H|D) \propto P(D,H)$ に当てはめます。

$$\begin{aligned} P(H = p|D = y) \propto& P(D = y,H = p)\\ =& P(D = y|H = p) \times P(p)\\ =& Bern(y∣p) \times Uniform(0, 1) \end{aligned}$$

PyMCやNumPyroのプログラミングは、右辺の最後の式を後ろから記述します。

def model_Bernoulli(N, Y = None):
    '''
        第4章のくじ引きの確率モデル(ベルヌーイ分布)
    '''
    # 確率 $p$ の事前分布は一様分布 $[0,1]$ と仮定する
    p = numpyro.sample("p", dist.Uniform(low = 0, high = 1))
    # くじ引きの結果 $y_{i} \ (i = 0, \cdots, 4)$ がベルヌーイ分布に従うと仮定する
    # ベクトル化(学習用データを確率変数に割り当てるためのNumPyroのお作法)
    with numpyro.plate("N", N):
        numpyro.sample("y", dist.Bernoulli(probs = p), obs = Y)

作成したモデルをプロットします。

model_args = {
    "N": len(Y),
    "Y": Y
}
try_render_model(model_Bernoulli, render_name = "くじ引き(ベルヌーイ分布)", **model_args)

4.4 ベイズ推論(サンプリング)

Step 3. サンプリング
ユーティリティ関数を使ってサンプリングを行います。

model_args = {
    "N": len(Y),
    "Y": Y
}
idata = run_mcmc(
    model_Bernoulli,
    num_chains = 4,
    num_warmup = 1000,
    num_samples = 1000,
    thinning = 1,
    seed = 42,
    target_accept_prob = 0.8,
    log_likelihood = False,
    **model_args
)

4.5 ベイズ推論(結果分析)

結果分析からは書籍とほぼ同じコードです。
PyMCのサンプリング部分をNumPyroに書き換えても同じようにコードを実行できるのがオブジェクト指向プログラミングの強みです。

Step 4. 結果分析

4.5.1 plot_trace関数

サンプリングが上手いったのかを確認します。
右側のプロットに傾向が見られない場合良いサンプリングができています。

az.plot_trace(idata, compact = False)
plt.tight_layout()

4.5.2 plot_posterior 関数

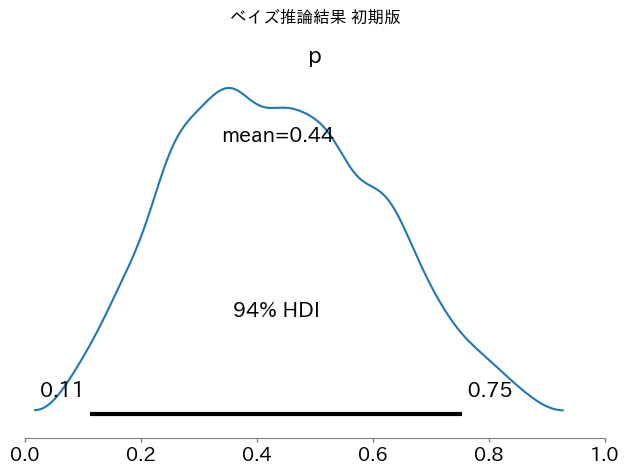
くじ引きの確率 $p$ の事後分布をプロットします。
5回中2回すなわち40%の割合で当たりがでた結果を反映して、くじ引きの確率は40%付近であると推定されました。

ax = az.plot_posterior(idata)
ax.set_xlim(0, 1)
plt.suptitle("ベイズ推論結果 初期版")
plt.tight_layout()
plt.show()

4.5.3 summary関数

テーブルデータで事後分布の概要を知りたい場合があります。
そのときに活躍するのがsummary関数です。

summary = az.summary(idata)
display(summary)

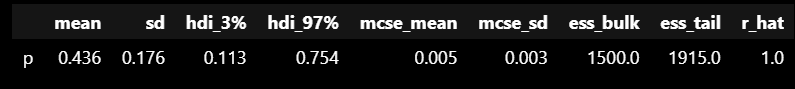
4.6 ベイズ推論(二項分布バージョン)

くじ引きの結果を集計したデータで分析する場合を考えます。
$n$ 回中 $y$ 回当たりを引いた場合を考えるということになります。

まず、前回の結果が次回に一切影響しない、かつ確率が一定のくじ引きであると仮定しました。
当たりを引いた回数 $y$ は二項分布に従うと仮定するのが自然です。

$$y \sim Bi(y|p, n)$$

次に、くじ引きの確率の推論精度を高める情報はありません。
そのため、確率 $p$ の事前分布は一様分布 $[0,1]$ と仮定するのが無難です。

$$p \sim Uniform(0, 1)$$

ここまでの結果を条件付確率の比例式に当てはめます。

$$\begin{aligned} P(H = p|D = (y, n)) \propto& P(D = (y, n),H = p)\\ =& P(y, (n, p))\\ =& P(y|(n, p)) \times P(n, p)\\ =& P(y|(n, p)) \times P(p) \times P(n)\\ \propto& P(y|(n, p)) \times P(p)\\ =& Bi(y|p, n) \times Uniform(0, 1) \end{aligned}$$

ベルヌーイ分布のときと同様にNumPyroのモデルを作成します。

def model_Binomial(n, y = None):
    '''
        第4章のくじ引きの二項分布モデル
    '''
    # 確率 $p$ の事前分布は一様分布 $[0,1]$ と仮定する
    p = numpyro.sample("p", dist.Uniform(low = 0, high = 1))
    # 二項分布のパラメータを明示的にプロットするための処理
    n = numpyro.deterministic("n", n)
    # 当たりを引いた回数 $y$ は二項分布に従うと仮定する
    numpyro.sample("y", dist.Binomial(total_count = n, probs = p), obs = y)

ベルヌーイ分布のときと同様にユーティリティ関数を使ってサンプリングを行います。

y = len(Y[Y > 0])
model_args = {
    "n": len(Y),
    "y": y
}
try_render_model(model_Binomial, render_name = "くじ引き(二項分布)", **model_args)

サンプリングと結果分析も同様に行います。

y = len(Y[Y > 0])
model_args = {
    "n": len(Y),
    "y": y
}
idata = run_mcmc(
    model_Binomial,
    num_chains = 4,
    num_warmup = 1000,
    num_samples = 1000,
    thinning = 1,
    seed = 42,
    target_accept_prob = 0.8,
    log_likelihood = False,
    **model_args
)

事後分布をプロットします。
くじ引きの確率 $p$ を知りたいので $p$ を選択してプロットします。

ax = az.plot_posterior(idata, var_names = ["p"])
ax.set_xlim(0, 1)
plt.suptitle("ベイズ推論結果 二項分布版")
plt.tight_layout()
plt.show()

summary = az.summary(idata, var_names = ["p"])
display(summary)

4.7 ベイズ推論(試行回数を増やす)

さらにくじを引いて50回中20回あたりがでた場合を試してみます。
事後分布がさらに狭くなって「確信が高まった」ことがわかります。

model_args = {
    "n": 50,
    "y": 20
}
idata = run_mcmc(
    model_Binomial,
    num_chains = 4,
    num_warmup = 1000,
    num_samples = 1000,
    thinning = 1,
    seed = 42,
    target_accept_prob = 0.8,
    log_likelihood = False,
    **model_args
)

ax = az.plot_posterior(idata, var_names = ["p"])
ax.set_xlim(0, 1)
plt.suptitle("試行回数を増やす (n=50)")
plt.tight_layout()
plt.show()

summary = az.summary(idata, var_names = ["p"])
display(summary)

4.8 ベイズ推論(事前分布の変更)

書籍のままだと変化が小さいので、数値を変えます。
あなたがくじを引く前に友人がくじ引きを行って10回中2回当たりを引いたと聞いていたとします。
友人の後に最初の例と同様にあなたは5回中2回あたりを引きました。
この場合のくじの確率 $p$ を推論してみます。

友人の試行によって確率の範囲を絞ることができそうです。
くじの確率 $p$ の事前分布は 一様分布 $[0,1]$ から $[0,0.4]$ くらいにせばめてもよさそうです。

事前分布の範囲を修正した確率モデルを作成します。

def model_Binomial_modified(n, y = None):
    '''
        前節の二項分布モデルに関して、当たりの確率の事前知識があった場合のモデル
    '''
    # 確率 $p$ の事前分布である一様分布の値域を事前知識に基づいて修正する。
    p = numpyro.sample("p", dist.Uniform(low = 0, high = 0.4))
    # 二項分布のパラメータを明示的にプロットするための処理
    n = numpyro.deterministic("n", n)
    # 当たりを引いた回数 $y$ は二項分布に従うと仮定する
    numpyro.sample("y", dist.Binomial(total_count = n, probs = p), obs = y)

# 4.6節と同じ試行回数で検証する。
y = len(Y[Y > 0])
model_args = {
    "n": len(Y),
    "y": y
}
idata = run_mcmc(
    model_Binomial_modified,
    num_chains = 4,
    num_warmup = 1000,
    num_samples = 1000,
    thinning = 1,
    seed = 42,
    target_accept_prob = 0.8,
    log_likelihood = False,
    **model_args
)

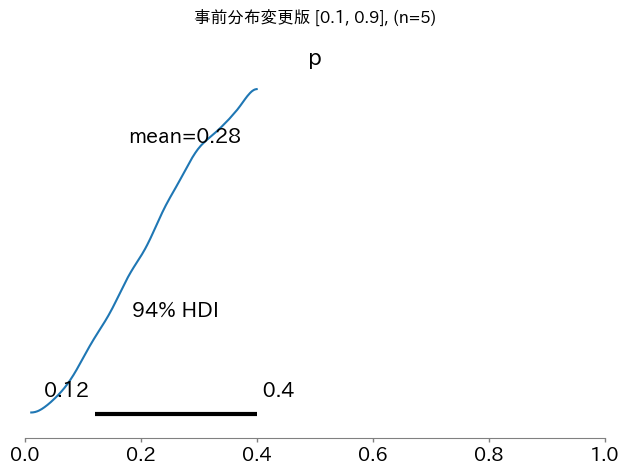
事後分布をプロットすると友人が当たりを引いた割合(20%)と高くあなたが当たりを引いた割合(40%)の間の値の可能性が高そうです。
互いに試行回数が少ないので中間の結論になったのだと考えられます。
ベイズ推論はこのように事前の情報とデータを組み合わせた推論を行うことができます。

ax = az.plot_posterior(idata, var_names = ["p"])
ax.set_xlim(0, 1)
plt.suptitle("事前分布変更版 [0.1, 0.9], (n=5)")
plt.tight_layout()
plt.show()

summary = az.summary(idata, var_names = ["p"])
display(summary)

4.9 ベータ分布で直接確率分布を求める

PyMCのコードではないので省略します。

終わりに

シンプルな例を使ってベイズ推論を行うことができました。
複雑な事象であってもこの例と同じ流れで問題に挑むことができる一貫性がベイズ推論の人気の理由の一つです。
奥深い世界を味わう助けになれば幸いです。