RSフリップフロップでブール代数演習

インバータ付きNAND型RSフリップフリップ(RSFF)回路について、代数的計算の練習になりそうだったので備忘録的にまとめてみます。

ど素人なので間違えてる可能性は大いにあります。指摘大歓迎です。

記号定義

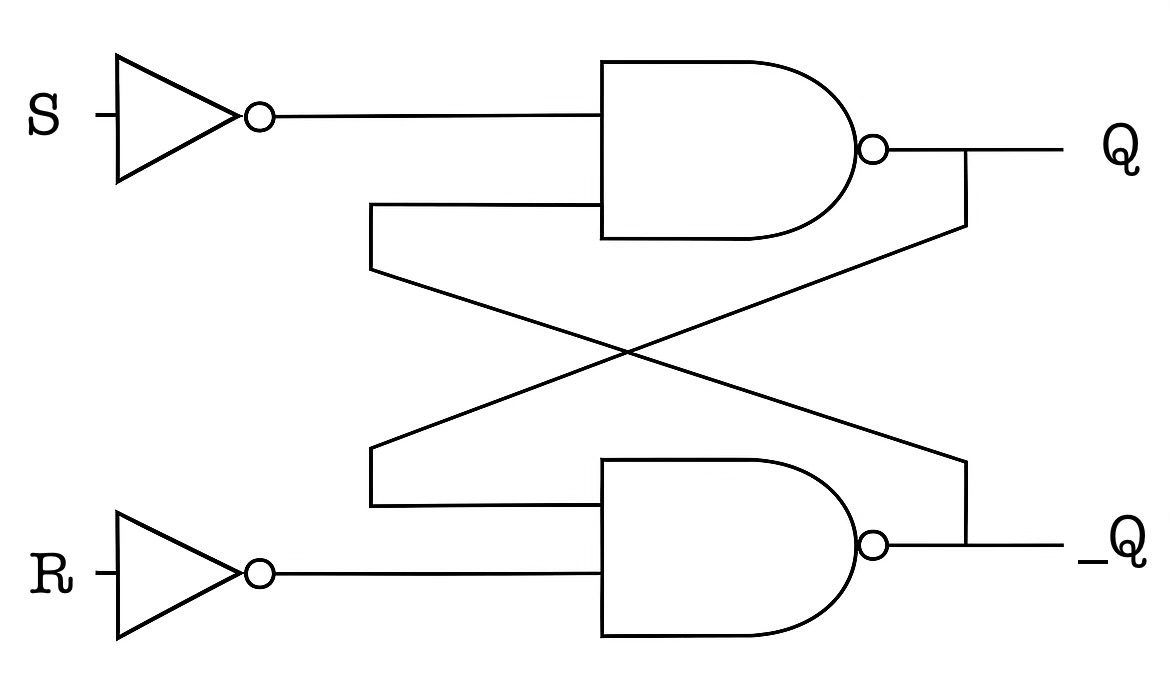
インバータ付きNAND型RSフリップフロップ(RSFF)回路

演算記号

• $X+Y\text{ : }X\text{ OR }Y$
• $X\cdot Y\text{ : }X\text{ AND }Y$
• $\overline{X} = \neg X\text{ (}X\text{の否定)}$

文字の定義

• $S,R\text{ : RSFFの入力}$
• $Q,\_Q\text{ : RSFFの現在の出力}$
• $Q^+,\_Q^+\text{ : RSFFの次の出力}$

前提となる論理式

回路

• $Q^+=\overline{\overline{S}\cdot\_Q}$
• $\_Q^+=\overline{\overline{R}\cdot Q}$

相補条件

• $\overline{Q}=\_Q$
• $\overline{Q^+}=\_Q^+$

この記事の趣旨

RSFFの真偽値表は以下のようになります。

$S$	$R$	$Q^+$
0	0	保持
0	1	0
1	0	1
1	1	不定

この真偽値表は、SとRに実際に当てはめて、論理回路を追跡したり、上記の論理式に代入したりして簡単に描くことができますが、これをブール代数の演算によって求めてみよう、というのがこの記事の趣旨です。すなわち、RSFFを解くという意味では無駄が非常に多いですが、ブール代数の練習にはちょうどよさそう程度のものです。

おもなブール法則

結合法則

• $A+(B+C)=(A+B)+C=A+B+C$
• $A\cdot (B\cdot C)=(A\cdot B)\cdot C=A\cdot B\cdot C$

分配法則

• $A+(B\cdot C)=(A+B)\cdot(A+C)$
• $A\cdot (B+C)=(A\cdot B)+(A\cdot C)$

吸収法則

• $A+(A\cdot B) = A\cdot (A+B) = A$

ド・モルガンの法則

• $\overline{A\cdot B} = \overline{A}+\overline{B}$
• $\overline{A+B}=\overline{A}\cdot\overline{B}$

S·R=0を導く

$$\begin{cases} Q^+=\overline{\overline{S}\cdot\_Q} \\ \_Q^+=\overline{\overline{R}\cdot Q} \end{cases}$$

のもとで

$$\begin{cases} \overline{Q} = \_Q \\ \overline{Q^+} = \_Q^+ \end{cases} \quad \Longrightarrow \quad S \cdot R = 0$$

となることを示します。

$\overline{Q}=\_Q$より

$$Q^{+} =\overline{\overline{S}\cdot\_Q} = S + Q \tag{1}$$

$\overline{Q^{+}}=\_Q^{+}$と $\_Q^{+}=\overline{\overline{R}\cdot Q}$より両辺を否定して

$$Q^{+} = \overline{\overline{\overline{R}\cdot Q}} = \overline{R}\cdot Q \tag{2}$$

$(1),(2)$より

$$S + Q = \overline{R}\cdot Q$$

両辺に$R$を乗じて

$$(S + Q)\cdot R = (\overline{R}\cdot Q)\cdot R$$

右辺は $\overline{R}\cdot R = 0$ によって $0$ となるので、左辺を展開して

$$S\cdot R + Q\cdot R = 0$$

両辺にさらに$S$を乗じて

$$S\cdot\bigl(S\cdot R + Q\cdot R\bigr) = S\cdot 0 = 0$$

左辺は

$$\begin{aligned} &S\cdot S\cdot R + S\cdot Q\cdot R \\ &= S\cdot R + S\cdot Q\cdot R \\ &= S\cdot R \\ \end{aligned}$$

したがって

$$S\cdot R = 0$$

状態遷移式の導出

$Q,S,R$と$Q^+$を結びつける式

$$Q^+=S+(\overline{R}\cdot Q)$$

を導出します。

$(2)$を繰り返し用いて

$$\begin{aligned} Q^+ &= \overline{R}\cdot Q \\ &= \overline{R}\cdot \overline{R} \cdot Q \\ &= \overline{R}\cdot Q^+ \end{aligned} \tag{3}$$

$S\cdot R = 0$、$R+\overline{R}=1$より

$$S=(R+\overline{R})\cdot S = \overline{R}\cdot S$$

よって

$$\overline{R} = \overline{R}\cdot (S+1) = S+\overline{R} \tag{4}$$

$(3)$は$(1),(4)$から

$$\begin{aligned} Q^+&= \overline{R}\cdot Q^+ \\ &= (S+\overline{R})\cdot (S+Q) \\ &=S+(\overline{R}\cdot Q) \\ \end{aligned}$$

この式に代入することで、（禁止状態$S=R=1$以外の）$Q^+$を$Q$から得られます。