Zenn
Open47

未知盆栽.hs

toyboot4etoyboot4e

この投稿は

競プロ・ Haskell 関連のスクラップです。ヒューリスティックや高度典型、手付かずのトラブルシューティグをやっていきます。

toyboot4etoyboot4e

[WIP] デバッガでランタイムエラーを掘り下げる

どこでプログラムが死んだのか知りたい

次の関数を呼ぶと例外が出ますが、メッセージからは例外の発生箇所がわかりません。コンテスト本番で謎の例外が出たらナイトメアです。 2 分探索する他ありません。

testFunc :: IO ()
testFunc = do
  let !_ = testBit (0 :: Int) (-1 :: Int)
  return()

 ghci> testFunc
 *** Exception: arithmetic overflow

コンパイラの設定で強制的にトレースを出すこともできる はず ですが、失敗しています。ひとまずデバッガの利用を考えてみます。

ghci からのデバッガの利用

ghci の基本的な機能は以下から伺えます:

http://www.kotha.net/ghcguide_ja/7.0.4/ghci-debugger.html

オプションを設定すると、例外発生時に強制的に breakpoint に入り、実行履歴 (:hist) が追えるようです:

ghci> :set -fbreak-on-exception
ghci> :trace testFunction
Stopped in <exception thrown>, <unknown>
_exception :: e = GHC.Exception.Type.SomeException
                    GHC.Exception.Type.Overflow
[<unknown>] ghci> :hist
-1  : testFunction:(...) (/home/tbm/dev/hs/abc-hs/arc179/c/Main.hs:22:12-41)
-2  : testFunction:(...) (/home/tbm/dev/hs/abc-hs/arc179/c/Main.hs:21:12-14)
-3  : testFunction (/home/tbm/dev/hs/abc-hs/arc179/c/Main.hs:(20,16)-(23,11))
<end of history>

これで十分かもですが、各変数の値を確認したいところです。 TODO: watch?

RST の -xc オプションを利用する

WIP

stack における設定方法

cabal における設定方法

エディタからの利用 (DAP)

WIP

toyboot4etoyboot4e

[DONE] 区間を set で管理するテクニック

概要

(区間, 値) の集合を管理し、 lookup/insert/delete を償却 O(\log N) で処理します (たぶん) 。この操作に副作用を持たせると PAST 6 M - 等しい数 があっさり解けます。実装は以下を参考にします。

https://noimi.hatenablog.com/entry/2021/05/02/195143

C++ 実装の強み

C++ の set は upper_bound がイテレータを返すのがナイスです。計算速度も良いかもしれません ( O(N \log N) ではなく償却 O(N) かも？しれません):

          [-----------------------]   挿入する区間
      [-----][----][----][---][----]  影響する区間の列
          ^     ^
          |     +-- upper_bound
          +-- prev(upper_bound) or lower_bound

emplace_hint が償却定数時間というのも良さそうです。 Range のマージ処理が高速になります。

Haskell で実装してみる

set よりも map を使うことにしました。比較がシンプルになると思います。ひとまず insert のみ実装してみました。

PAST 6 M - 等しい数

これで良い気はしますが、倍速程度には速くなって欲しい気もします。

高速化の試み

containers 前提で様々な型の組み合わせを試してみます。

データ型 キー型 値型 結果
Map (Int, Int) a 1254 ms
Map Int (Int, a) 1254 ms
Map Int (Int, a) 1274 ms
IntMap (Int) (Int, a) 1106 ms

全然速くなりませんでした。 再提出すると実行時間がブレるので、どれも同程度に思えます。一応 IntMap にしておきます。

INLINE は指定しない方が速かった です。この辺も全然分かりませんね。 同じコードを再提出したときに実行時間がブレブレでした。謎です。

他の問題への提出

潰しが効くデータ型なので、活用できるよう備えておきたいところです。

  • ABC 330 E - Mex and Update
    1715 ms. やはり座標圧縮した方が速いようです。

    RangeMap をラップした RangeSet の関数は INLINE にしてみました。効いているのかは謎です。

quickcheck

愚直解と比較する quickcheck を書いてみました。テストの書き様はともかく、 RangeMap の内部実装は問題無さそうです。

$ cabal test --test-show-details=direct --test-options="--quickcheck-verbose"
$ cabal test --test-options "--quickcheck-tests 1000"

課題

  • 内部のマップ型をより高速なものに変更したいところです。
  • RangeMap は不変データ型ですが、 StateT に載せると合成が厄介になります。より手軽なモナドが欲しいところです。
toyboot4etoyboot4e

[TODO] 型推論の理由を調べる方法

Haskell のデバッグに朦朧とする時間は今も大して減っていません。型表記を書くと、コンパイラの型推論と自分の中で思っていた型が不一致であると気づけます:

src/past06-m.hs:185:14: error:
    • Couldn't match type ‘RangeMap Int’ with ‘Int’
      Expected: RangeMap Int
        Actual: RangeMap (RangeMap Int)
    • In the expression: fromVecMRM xs onAdd :: RangeMap Int
      In an equation for ‘rm0’:
          !rm0 = fromVecMRM xs onAdd :: RangeMap Int
      In the expression:
        do n <- int'
           xs <- intsU'
           q <- int'
           lrxs <- U.replicateM q ints110'
           ....
    |
185 |   let !rm0 = fromVecMRM xs onAdd :: RangeMap Int
    |              ^^^^^^^^^^^^^^^^^^^

さらに一歩踏み込んで、なぜこのように推論されたのか、山勘ではなく機械的に調べる方法がほしいです。

あ……今回の件は let .. = を ... <- に置き換えて直りました……:

  (!rm0 :: RangeMap Int) <- fromVecMRM xs onAdd
toyboot4etoyboot4e

[TODO] 正確評価に関連した塩漬けの疑問

Bind される変数を正格評価する意味はあるか

たとえば Control.Monad.Trans.State.modifyM は lazy 版と同じ実装になっていますが、 ! は必要ないのでしょうか。

-- | A variant of 'modify' in which the new state is generated by a
-- monadic action.
modifyM :: (Monad m) => (s -> m s) -> StateT s m ()
modifyM f = StateT $ \ s -> do
    s' <- f s
    return ((), s')
{-# INLINE modifyM #-}

IO, ST 以外のモナドが逐次実行されるのか、イマイチ確信が持てず……。単なる関数に展開されるなら、引数に ! をつけたほうが良さそうなものですが。

Fusion 狙いなら正格評価しない方が良い？

気になります！

2 回正格評価すると処理速度は落ちるのか

気にせずバンバン ! を書いて良い？

正格なタプルを使ったほうが速くなるのか

T2 型を用意しました。

  • Set や Map に保存する場合、キーにする場合
    Map のキーにした場合、 全くスピードは変わりませんでした 。
  • unboxed vector に保存する場合

Map の中ではどのように遅延評価が溜まっていくのか

気になります！　というか内部も正格な Map が欲しい。

toyboot4etoyboot4e

[TODO] ネストした StateT をフラットに扱いたい

つまり lift したくないのですが……？

toyboot4etoyboot4e

[TODO] INLINE しない方が速いのはなぜか

たとえば

  • 再帰関数
  • 巨大な関数
  • where 句の中の関数

そもそも同じコードを提出した際に実行時間がバラバラなので INLINE が効いているのか分からない問題はあります。

INLINE した方が極端に速いのはいつか

Mo の時は極端に効いた気がします。 Fusion が効く場合もそう？

stToPrim が効くのはいつか

toyboot4etoyboot4e

[DONE] Z-function

Z-function - Algorithms for Competitive Programming

\begin{aligned} z[0] &:= 0 \\ z[i] &:= \mathcal{lcp}(s[0:], s[i:]) \end{aligned}

これはサクッっと理解できそうです。結局ローリングハッシュが強そうな雰囲気もありますが、 ACL にも入っているので履修しておきます。

O(N^2) 実装

上の式を愚直に計算します。

-- | \(O(\max(N, M))\) Longest common prefix calculation.
lcpOf :: BS.ByteString -> BS.ByteString -> Int
lcpOf bs1 bs2 = length . takeWhile id $ BS.zipWith (==) bs1 bs2

-- | \(O(N^2)\) Z function calculation.
zOfNaive :: BS.ByteString -> U.Vector Int
zOfNaive bs = U.generate (BS.length bs) z
  where
    z 0 = 0
    z i = lcpOf bs (BS.drop i bs)

O(N) 実装

まず大体のイメージ:

下側の青い箱の部分は z-box とか rightmost segment matches などと呼ばれており、これを状態として持ちつつ z[1], z[2].. を求めて行きます。

O(N) になる証明

Match する回数が最大 N回、マッチに失敗する回数も最大 N 回です。よって O(N) です。

Haskell 実装

実装しました。 constructN を使うと z-box を状態として持てなかったため、 cojna/iota と同じく可変配列に手動で書き込むことにしました。

https://github.com/toyboot4e/toy-lib/blob/main/src/Data/ByteString/ZFunction.hs

toyboot4etoyboot4e

[DONE] Suffix array

Suffix Array - Algorithms for Competitive Programming

\mathcal{sa}: ソート後の添字 \mapsto 元の添字

これを実装すれば、 ACL も残すところ CRT と floor sum のみです。

O(N^2 \log N) 実装

愚直に実装します:

-- | \(O(N^2 \log N)\) Suffix array calculation.
saOfNaive :: BS.ByteString -> U.Vector Int
saOfNaive bs =
  U.convert
    . V.map fst
    . V.modify (VAI.sortBy (comparing snd))
    $ V.generate n (\i -> (i, BS.drop i bs))
  where
    n = BS.length bs

O(N \log N) 実装 (ダブリング)

困難は実装せよ……！　写経を通じて理解しました。

https://github.com/toyboot4e/toy-lib/blob/main/src/Data/ByteString/SuffixArray.hs

[SKIP] O(N) 実装 (SA-IS)

これは大変そうなので飛ばします。

LCP array (Kasai's algorithm)

  • min 演算子による lcp 配列上の LCP 値の畳み込みが \mathcal{lcp}(p[i], p[j]) になる
  • 逆に言うと SA 上の隣接 2 項の LCP が最も大きい

これを活かして長い suffix から順に LCP 配列上の値を確定させます。

TODO: O(N) の証明

toyboot4etoyboot4e

[TODO] Convex Hull Trick / Li-Chao Tree

そろそろ EDPC を全完したいです。

参考資料

参考コード

IntMap による実装例:

https://atcoder.jp/contests/dp/submissions/31619243

Seq による実装例:

https://atcoder.jp/contests/dp/submissions/30568053

実装

WIP

toyboot4etoyboot4e

[TODO] Aho-Corasick

文字列はこのぐらいまでやっておけば一般人としては十分なのではないかと。

toyboot4etoyboot4e

[TODO] 鉄則本のヒューリスティック問題

ヒューリスティックの訓練は、鉄則本 → AHC 033 → Thunder 本の順にやっていきたいと思います。 kaede さんのブログ も参考にしつつ、後は短期コンを中心にひたすら過去問でしょうか。

toyboot4etoyboot4e

[DONE] Floor sum (unsigned)

ALPC 制覇を目指して……！

問題

y = (ax + b) / m (a \ge 0, b \ge 0), y = 0, x = 0, x = n - 1 に囲まれる格子点の数を O(\log ma) で求めよ。

概要

フレンズさんの解説で大まかな処理が見えました。互助法になるとか mod が出てくるのが理解できません。うーむ

https://x.com/kyopro_friends/status/1304063876019793921?ref_src=twsrc^tfw|twcamp^tweetembed|twterm^1304063876019793921|twgr^1b902bab1651f9656a188044d9c176a6d7f04a95|twcon^s1_&ref_url=https%3A%2F%2Fdrken1215.hatenablog.com%2Fentry%2F2022%2F12%2F14%2F235718

この記事が詳しくて良さそうです。

https://qiita.com/AkariLuminous/items/3e2c80baa6d5e6f3abe9#4-floor_sum

考察

上の Qiita 記事をじっくり読んで納得しつつあります。中学数学が難しい……

リファレンス実装

やはり cojna さん……！

https://atcoder.jp/contests/practice2/submissions/16567211

実装

式変形で納得していない部分もありつつ、ひとまず AC しました。

https://atcoder.jp/contests/practice2/submissions/54777651

→ 完全に理解した！　NTT でも思いましたが、離散化は周期性を伴うものかもしれません。

Floor sum (signed)

a \ge 0, b \ge 0 の成約を消す処理があります。ここは一旦、考察 0 の完全な写経で通過させてもらいます……

toyboot4etoyboot4e

[DONE] Wavelet Matrix (1)

魔術的なクエリ処理ができる心惹かれるデータ構造です。完備な辞書だとかビットベクトルだとか。動的に処理する場合は wavelet tree の方が必要らしいです。

問題

情報源

眺めただけ

Web 記事はこの辺が良さそうです。しかしトップダウンの網羅的な教科書風記事は中々見つからない気がします。他の情報源も必要です。

書籍はどうせ Wavelet Matrix の話しか読まないので、持て余す気がしてしまいます。

結局、元ネタの論文を読んでのが安心かもしれません:

いや難しいな……

インプット実施

Wavelet Tree の概要

テキストが頭に入ってこないので、動画を観てみました。最低限の情報に絞ったインプットとなっており良かったです:

https://m.youtube.com/watch?v=4aSv9PcecDw&pp=ygUOd2F2ZWxldCBtYXRyaXg%3D

内容は Wavelet Tree でした:

  • Wavelet tree は値域の 2 分木

    • セグメント木は変域 (添字) で 2 分していく
    • Wavelet tree は値域で 2 分していく。各ノードには数列が値域でフィルタリングされた結果が残る。順序は保つ。
      • 深さは log A だが座標圧縮すれば log N になる

  • 行 (bit) 毎に 2 つの配列を持つ

    • 2 分岐における大小比較 bit 列(Int -> Bool)
    • 2 分岐における大小比較 bit の累積和 (区間中の左右への分岐数が分かる)

  • クエリ処理

    • select, rank (完備辞書)
      • [l, r] 中の x の数 (rank l r x, freqIn l r x)
        根まで降りて累積和の差？　座標圧縮済みなら初めから根から始めれば良い気がする
      • [l, r] 中の kth skallest (select k)
        累積和を使って左右分岐して突き止める。
    • swap(i):
      i, i + 1 を入れ替える。累積和の更新のためセグメント木か BIT を使う

Wavelet Matrix の詳細

Wavelet Tree のデータの持ち方が謎です。頂点に列を載せるには？　これは Wavelet Tree を飛ばし、 Wavelet Matrix の紹介で理解できました。

https://miti-7.hatenablog.com/entry/2018/04/28/152259

基数ソート (i bit 目での安定ソート) で順序を保ってフィルタリングしていることが分かりやすい！　Access で値の復元が必要なのは wavelet matrix ならではですね。座標圧縮と組み合わせて使えそうです。

実装

ソースを読んで見る

Nyaan さんのライブラリを読みました。実装や API もかなり素直で、学習教材として良かったです。

https://github.com/NyaanNyaan/library/blob/8fcf379daa5b49f9c20ba6a97a6047d7c0e80a39/data-structure-2d/wavelet-matrix.hpp

Haskell においては bitvec を使うと U.Vector Bit を packed なビット列として使用できます。

実装しました。よっしゃ！

疑問点

  • 添字を返すには
toyboot4etoyboot4e

[DONE] Wavelet Matrix (2)

問題演習

  • Static Range Frequency
    [l, r) 区間中の x の出現数を数えます。 [l, r) 区間中の x \in [xl, xr) の数でも解けます。

座標圧縮の自動化

これまでの WaveletMatrix を RawWaveletMatrix とし、座標圧縮済みのものを WaveletMatrix としました。これで咄嗟に C 問題で無双できるかもしれません。

API 強化

添字を返す select はあった方が良さそうです。すべて O(\log A) で動作します。

  • findKthIndex 配列中の k 番目の x の添え字を返す
    上から下へ降りて、最下段の配列中に連続した x を見つけます。その後上へ戻ることで元の添え字が分かります。配列中に存在しない x や k は上手く弾きます。 TODO: なぜ弾けているか？
  • lrFindKthIndex 配列の [l, r] 区間中の k 番目の x の添字を返す
    もちろん [l, r] 区間を絞って同様の処理を実施できます。
  • ikthMin 配列の [l, r] 区間中の k 番目に小さい値の (添字, 値) を返す
  • lookupLT, lookupGT
    freq の前後番目の値を kthMin で取得します。定数倍は重めです。

簡潔ビットベクトル

BitVector の簡単な実装としてはビット列 + ワード単位累積和がありますが、平方分割のアイデアで更に省メモリ化できそう？　N が巨大な問題で活躍しそうですが、 N が大きいと入出力で TLE しますよね。現在の競プロとは別に、ビッグデータ競プロが無いと活躍しない気がします。実装しません。

https://blog.tiramister.net/posts/bitvector/

https://miti-7.hatenablog.com/entry/2018/04/15/155638

さらなる API 強化

  • assocs (値, freq) のペアのリストを値の昇順で返す
    O(\log A \min(|A|, L)) 上から下へ DFS します。変域が狭い時のみ高速です。出番無しかも。
  • topFreqK (freq, 値) を freq の多いものから順に K 個を返す
    O(\log A \min(|A|, L) \log N) 枝刈りが聞きそうですが、実は最悪計算量が重いです。ヒープの計算量の \log N も付けときました。 assocs を freq でソートすれば良いので、実装しないことにしました。
  • intersect
    2 区間で共通して出現する値について (値, 頻度) を返す。やはりこれも遅いので実装しません。
toyboot4etoyboot4e

[DONE] Wavelet Matrix (3)

Segment Tree on Wavelet Matrix

参考

やはり Nyaan さんのコードが最小で学習に良かったです。

  • ps: sort . uniq $ xys
  • ys: sort . uniq $ ys
  • xid, yid: 座標圧縮 (ps, ys) を元に添字取得

https://nyaannyaan.github.io/library/data-structure-2d/segment-tree-on-wavelet-matrix.hpp

境界チェックは必要無いのか？

半開区間を使っていると、結果として境界チェックが必要無くなるっぽいです？

  • 座標圧縮列の範囲内であって列中の点に無い範囲 [l, r) の場合
    これは [l, r) 共にlower_bound で [l', r') に写せます (特に半開区間であるため)
  • 座標圧縮列の外側の範囲 [l, r] の場合
    • 座標圧縮列 < [l, r) の場合: [0, 0) が返ってくる
    • [l, r) < 座標圧縮列の場合: [n, n) が返ってくる

よくできていますね。僕は Haskell の慣習に従って閉区間で戦っているため煩雑になりました。

動作原理

これの解説記事が無くて困りました。

  • write/modify
    軌跡上の全点に操作します。畳み込みの際にダブルカウントしないかが不安ですが、非常に上手くやっています。
  • 可換群の畳み込み
    仕組みは freq と同じ です。各行の bit が ON の場合に OFF であった範囲 (左に降りた範囲) を 畳み込みます。これが結果として 2 次元の範囲の畳み込みになります。

注意点

畳み込みは \mathcal{upper} = 2^{\mathcal{height}} 時に正しく動きません。というか freq もそうだったのか？ yosupo さんや maspy さんはセグ木を 1 行追加して対処しています。僕は N が 2 べきの場合に行列に 1 行足して対処しています。

[TODO] 非可換群の畳み込み

verify 用の問題が無いかも。別にいいか。

遅い

何で遅いんでしょう。

応用的な verify

補集合を考えると、重複した点の数を数えれば良いです。重複する点を数えるためには、以下のように近隣の重複点の位置を WM に入れて freq で取り出せます:

--    input  *  .  .  *  .  *  .  *
--     last  0  1  2  3  4  5  6  7
--           -        0     3     5
--                    <-----> [3, 5] 中の x \in [3, 5] の数は 1
--                    <-----------> [3, 7] 中の x \in [3, 7] の数は 2
--

というのを人の提出から学びました。どうやれば思いつくんだ……

[TODO] 重複を無視した kth min

以下ブログで D-Query 永続と呼ばれるテクニックを学びたいです、

https://pekempey.hatenablog.com/entry/2016/05/16/235152

いや、もう少し説明を書いてくれ〜

toyboot4etoyboot4e

[DONE] Splay tree (1)

Link-cut tree の前準備として splay tree を作ってみます。定数倍がかなり遅いものの、償却 O(\log N) で多様な操作ができると評判の平衡木です。 Unboxed vector を使えば Haskell にしては速い木になる期待もあります。

参考

何を見るべきか調べるところから始めます。

その他

目標

次の関数を実装します: insert/delete/lookup/lookupLE, lookupGE. 区間クエリとか遅延評価は保留します。

不変条件

Splay tree は 2 分木のような形をしています。必ずしも平衡されているとは限りません。親子の key の大小関係は、通常の木と同じく左が LT 右も GT です。

大雑把な理解

Insert / lookup といった操作の度に、対象のノードを根まで持ち上げて行くようです (splay 操作) 。 Splay 操作には top-down と bottom-up の 2 種類あります。 Top-down の方が効率が良いです。

https://stackoverflow.com/a/65643843

Bottom-up な splay 操作

親配列かスタックが必要になります。定数倍も若干重めです。

Top-down なsplay 操作

Self-Adjusting Binary Search Trees に出てくる 他、 sile/splay_tree もこの実装のようです。 sile/splay_tree におけるデータの持ち方は以下です:

  • 各 node は親情報を持ちません。 Top-down splaying の効率面の有利さが察せられます。
  • 各 node は密な vector に保存されます。要素削除は swap_remove 的な操作で上手くやっているらしく、空きスロットはありません (配列の頭の方に値が詰められています) 。
  • イテレーションは DFS や BFS です。密なデータ列を、しかし飛び飛びで走査します。

Top-down splaying の詳細

Self-Adjusting Binary Search Trees に出てくる通り 、 top-down splaying においては L/R Tree のルートおよび単点、 mid tree のルートを持って、 2 つずつノードを降って行きます。 Zig-zig の場合は rotation を行います。このとき Grand child の親と sibling は grand child から切り離し、 L/R tree にくっつます。

以下の不変条件を考えると整理がつきました。

  • L tree: key(l) <= key(currentNode). 重複が無いのでkey(l) < key(currentNode) か……
  • R tree: key(r) > key(currentznode)
  • rightChild(leftTree) = null
  • leftChild(rightTree) = null

PDF 中の擬似コードでは null(left), null(right) が暗黙的に L/R tree のルートを指すのが厄介な気がします。

Semi-splaying

Splaying の zig-zig ケースの定数倍を良くしますが、最悪ケースでは必ずしも速いと言えないようです。今回は見送りますか……。

写経・実装

困難は実装せよということで、やっていきましょう……！

  • splayBy
    PDF を参考に実装しました。 null をキーとして L/R 木のルートを持っているのが厄介ですが、他は素直で良いコードでした。何をしているのか分かりません……。
  • insert
    Splay してからルートを挿入します。 REPL やランダムテストによってエラーケースを見つけて直しました。
  • lookup
    Splay してからルートを返すだけです。
  • delete
    Splay 後、ルートを切り離した 1 本の木に仕立てます。左右端に splay すると、新 root の左 (右) の子が null になることを活かします。
  • LT, LE, GT, GE
    Splay によって見つかるノードは、目的の key に隣接したノードです。それが目指す側 (LT, GT) にあれば採用します。目指す側に無い場合は頑張って splay して目的のノードを見つけます。

verify

Library Checker にちょうど良い問題があります。結果は、 unboxed vector を使ったにも関わらず IntMap よりも遅い！

一応実装できました。現在は単に性能の悪い木ですが、これからどのように活躍してくれるのでしょうか。楽しみです。

toyboot4etoyboot4e

[DONE] モジュール単位でライブラリを埋め込む

Haskell longest コードゴルフ王者 (200 KB) を止めたい。手元ではローカルのライブラリとして toy-lib を読み込み、提出時に埋め込みます。

-- toy-lib {{{
import ToyLib.Prelude
-- }}}

埋め込みの機能は既にあるものの、 ABC 用プロジェクトとの相性を高めたいです。

Stack script はローカルライブラリを読み込めない仕様である

この方式だと script 実行の前にも埋め込みが必要になります。

https://github.com/commercialhaskell/stack/issues/5305

Stack/Cabal プロジェクト間でパッケージのバージョンを揃えるのも面倒ですし、もう cabal プロジェクトとして常にネイティブコードにコンパイルしようと思います。

追記: リビルドが爆速になったため、 stack script である必要も無くなりました。

oj

埋め込み版のプロジェクトをコピーして作るのが無難そうです。コピーや埋め込み処理が必要な他、非パスも変わるためスクリプトの更新が必要です。

提出ファイル変更

atcoder-cli のテンプレートを変更しました。提出直前に作成した .submit.hs を提出します。

{
    "task": {
        "program": [
            "Main.hs"
        ],
        "submit": ".submit.hs"
    }
}

ライブラリ

コンテスト用の bulk imports モジュールを作成しました:

ToyLib.Contest.Prelude
-- | Bulk imports and re-exports for contest.
module ToyLib.Contest.Prelude
  ( module Data.Vector.Extra,
    module Data.Vector.IxVector,
    module ToyLib.Debug,
    module ToyLib.Parser,
    module ToyLib.Prelude,
    module ToyLib.ShowBSB,
  )
where

import Data.Vector.Extra
import Data.Vector.IxVector
import ToyLib.Debug
import ToyLib.Parser
import ToyLib.Prelude
import ToyLib.ShowBSB
toyboot4etoyboot4e

成果

  • Main.hs のリビルドが爆速になった
    ライブラリ部分は一度しかビルドしなくなった模様です。非常に良いです。
  • 提出ファイルが小さくなった
    事前 import 部分を最小化して提出ファイルが小さくなりました。まだデカいですが。

後は初回ビルドを高速化したいです。 Haskell 版 sccache が欲しい……？

toyboot4etoyboot4e

[DONE] Splay tree (2)

前回は IntMap 似の SplayTree を作ってしまいましたが、今回は列 (seq) を載せるための SplayTree を作り直します。言わば SplaySeq.

写経

Node に親を載せたくない？　Top-down splaying がしたい？

愚問ですぞ！！！　今回は写経します。読解さえ後回しにします。

https://maspypy.github.io/library/ds/splaytree/splaytree.hpp

写経メモ

  • 実装の共通化が上手い
    ノードのインスタンスに処理を振り分け、 splay tree の実装は 1 つで済んでいる。

  • Node& root (可変参照) がズルい
    Splay 木にアクセスする度にユーザが持つルートへの添字を更新したい。添字の更新をユーザから隠す仕組みが必要か。 → ラッパーを作りました。

  • 区間反転ができるのは可換モノイドだけ
    遅延要素は再計算不要とする。反転の実装は、貪欲に反転すれば良いです。 2 回反転する場合は反転をキャンセルします。ただ可換モノイド (または flip 可能なモノイド) のみで可能と思われます。

  • 何もしない instance SemigroupAction NoAction a が欲しい。
    一旦 lazy/strict な splay sequence で実装を共有するために欲しい。 instance (Semigroup a) => SemigroupAction a a と重なる。関数をフィールドに入れると遅い。 Segment Tree Beats でも思ったが、実装をダブらせたくない。 Zig の comptime が欲しい……。

Verify

参考

toyboot4etoyboot4e

上の投稿では、一言で言えば、『遅延伝播反転可能平衡二分木』を作っていますね。その実装には splay tree 以外にも色々ありえるようです。 AVL 木はもちろん、 treap や RBST が競技プログラミングではよく使用される雰囲気があります。にわかですが。

toyboot4etoyboot4e

[TODO] Splay tree で multiset

kth min までの畳み込みができます。

toyboot4etoyboot4e

[WIP] Link-cut tree

憧れのデータ構造です。

LCT を理解する

全然分からない。

写経・実装

maspy さんの link_cut_tree.hpp の写経を通じて仕組みを理解して行きます。

  • maspy さんのコードと比較して、 preferred path = heavy path で path-parent edge = light edge と言えそう。 Heavy/light は HLD からの連想かな。
  • 一通り実装してみた。
    • Underlying tree と auxiliary tree(s) があって名前が衝突しがち
    • expose されたノードの右に子は無い
  • verify で落ちる。 state の写経を修正して AC!

verify

4 問あります。一部は Top tree でも解けるとか。

toyboot4etoyboot4e

[TODO] Core

Core から分かりそうなこと

  • 末尾再帰の展開結果
  • サンクを使った再帰の評価
  • fusion が起きているかどうか
  • 正確評価
  • MagicHash 無しのコードがなぜ遅いか
  • Haskell の型引数は実行時に消えないこと (たぶん)
  • SPECIALIZE 指定の Haskell がなぜ遅いか

Core が読めれば Haskell の挙動を深く理解できるかも？

情報収集

toyboot4etoyboot4e

[DONE] Segment tree beats

区間 chmax, chmin を扱えるセグメント木を作ります。

https://smijake3.hatenablog.com/entry/2019/04/28/021457

概要

maspy さんの実装を見た限り、遅延セグメント木への変更は applyAtのみで、後はモノイド・作用素付きモノイドの実装でカバーできています。

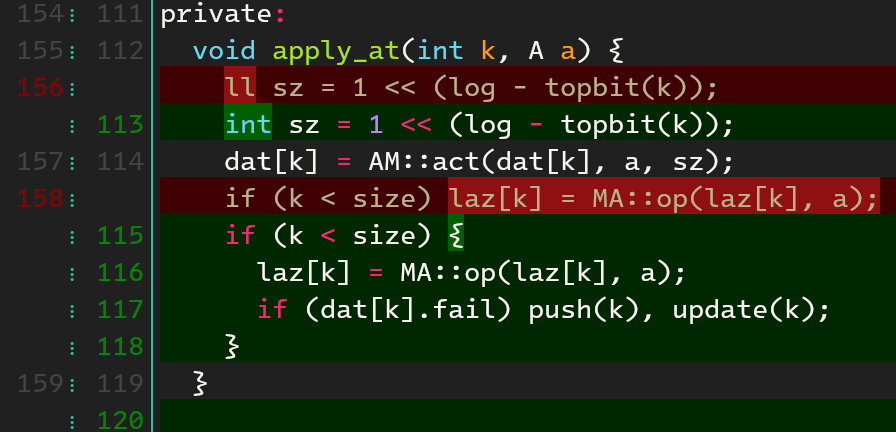
fail フラグとは区間に対する作用の適用の成功・失敗を表します。作用の適用に失敗した場合、すなわち遅延評価では正しく計算できない場合は、子要素に対し作用を適用し、改めて親要素を計算します。

https://rsm9.hatenablog.com/entry/2021/02/01/220408

maspy さんの遅延伝播セグメント木における定数倍高速化

maspy さんのセグメント木は手持ちのセグメント木 (PAST 上級本準拠) と実装が異なるため、先に詳細を読み解きます。 maspy さんの記事の図解がさり気なく PAST 上級本と異なり、枝刈りを表しています。

https://maspypy.com/segment-tree-のお勉強2

違い 1. 遅延値の違い

  • PAST 上級本: そのノード自身とその子に対する作用の遅延値を保存する
    • ノードへの作用は遅延される
    • 親ノードの値計算には (sact 子ノードの遅延値 子ノードの値) を使う
  • maspy さん: そのノードの子に対する作用の遅延値を保存する
    • ノードへの作用は即実施され、子ノードへの作用が遅延される
    • 親ノードの値計算には子ノードの値を使う (子ノードの持つ作用の蓄積値は孫に対して働くものであるため不要)

違い 2. 『(1) 上側から伝播』『(3) 上側を計算し直し』における枝刈り

maspy さんのブログで黄色に塗られた部分が PAST 上級本と異なります。

  • PAST 上級本: その葉のすべての親ノード
  • maspy さん: 畳み込みの計算に必要な区間の親ノードのみ

(1) 上側から伝播

prod (fold)

https://github.com/maspypy/library/blob/main/ds/segtree/lazy_segtree.hpp#L72

apply (sact)

https://github.com/maspypy/library/blob/ae783f093ffac1b12c584fb599865f25fa2260e0/ds/segtree/lazy_segtree.hpp#L91

(3) 上側を計算し直し

apply (sact)

https://github.com/maspypy/library/blob/ae783f093ffac1b12c584fb599865f25fa2260e0/ds/segtree/lazy_segtree.hpp#L102

以上の分岐のおかげで (2) の区間の 1 つ上のノードのみを伝播の対象にできています (スゴい……) 。したがって畳み込みの計算においては必要最小限の伝播を行います。

枝刈りの有無の比較結果

一長一短でした。

  • 作用が重い計算の場合: 枝刈りの方が速い (Affine2d など)
  • 作用が軽い計算の場合: PAST 上級本の方が速い (Sum, Max など)

言語や実装によっては常に枝刈りした方が速いかもしれません。

Segment Tree Beats へ

遅延セグメント木とコードが被る

遅延セグメント木とのコード共通化を避けました。 TODO: セグメント木専用の型クラスを用意して、常に fails を取得可能にすればコードを共通化できると思います。 Haskell の型クラスは動的なので、 Beats 以外のパフォーマンスは下がりそうですが。

モノイドの種類

  • maspy さんのライブラリでは SumMinMax - AddChminChmax が最も強く、他は機能制限版のようです。
    • minc, maxc: min count, max count でした。僕は nMax, nMin としました。
  • 実は区間 gcd も beats に載るとか。今回は見送ります。

結果

Library Checker が 1059 ms でした。

https://judge.yosupo.jp/submission/225971

toyboot4etoyboot4e

セグメント木専用の型クラスを追加

区間長を受け取る semigroup action のような型クラスを追加し、若干コードを共通化できました。ただ遅延セグ木と beats をゼロコストで共通化するのは Haskell では無理だと思います。

toyboot4etoyboot4e

[DONE] ポテンシャル付き Union-Find に群を載せる

型クラス Group を追加し、ポテンシャル付き Union-Find を抽象化しました。

経路圧縮の際は演算子を逆順に畳み込むことになるため、特に向きに気をつける必要があります。

toyboot4etoyboot4e

[TODO] その他 Union-Find

IntMap 製 Union-Find で十分ですが、一応……

Undoable Union-Find

部分永続 Union-Find

toyboot4etoyboot4e

Haskell 版 ACL が存在しない理由

Nim の ACL には Extra という名目で何でも入っているので、あれがやりたいです。

  • リストと vector, 関数と型クラスで好みに差が出る
    ライブラリがあっても趣味が合わない可能性大です
  • ACL の実装自体が難しい
    相当パフォーマンスを出していますから、実装するだけでも一苦労です
  • 半群作用を始めとした型クラスの準標準ライブラリが無い (ある？)
    ACL 専用のボイラープレートが無く、ユーザのライブラリと溶け合う仕組みが必要です
  • ローカルで使用する際に関数名が被らないようにバンドリングする機能が (まだ) 無い
    ローカルのライブラリで名前空間を切れるなら別に ACL が無くても良い (最悪、手元ですべてバンドリングすれば良い) です

やはり名前解決しつつ、名前衝突を避けてバンドリングする機能が必要です。それさえあれば、 ACL の完全体が無くても十分です。

toyboot4etoyboot4e

[DONE] SWAG (sliding window aggregation)

窓の中身の畳み込み (集約) を償却 O(1) で求めます。

セグ木で O(N \log N)

それでいいんじゃないかな……

Stack

左から右へ伸縮する窓の中の要素の畳み込みを答えます。尺取り法ですが、逆元の無い結合演算にも対応します。都度モノイドの双対 scanr を作成することで、逆元無しで O(N) を実現します。

ざっくりとしたメモですが、以下の図において

  • pushBack
    バッファに値 [7] を追加し、バッファの畳み込みを更新する
  • popFront
    双対右スキャンの左端 (<--) の値を削除する (※)
  • fold
    双対右スキャンの左端 (<--) の値 \diamond バッファの畳込み
　　　　　　　配列  [1]-[2]-[3]-[4]-[5]-[6]-[7]-[8]-..
　　　　　　　　窓  [---------------------]
　　　　　バッファ                  [5]-[6]
バッファの畳み込み                  *******
　　双対右スキャン  <--------------

(※) popFront で双対右スキャンが空になったとき、バッファ中の値を双対右スキャンへ移動します。償却 O(1) です。

Deque

基点から左右に Stack を持って、片側の Stack が無くなったら中点に移動し直すみたいです。実装は簡単ですが、償却計算量の証明が難しそうです。定数倍はやや重めですが、気にするほどでもないかも。

Deque 版で Stack の問題を解いてみる

187 ms から 219 ms に減速しました。

toyboot4etoyboot4e

[WIP] 名前解決して埋め込む

AtCoder でローカルのライブラリを qualified import して使えるようにしたいと思います。これがある意味で atcoder-hs の代わりになります。

やっとやる気になって来ました。多少なりとも Haskell 界隈に貢献したい！

名前解決の必要性

AtCoder の提出ファイルは Main.hs 単ファイルです。 Haskell ではファイル内でスコープを切る機能がありませんから、たとえば A.f と B.f を単純に 1 つのファイルにまとめると衝突します。

回避策は主に 2 つです。

  1. あらかじめ衝突しない名前を付けておく
    たとえば A_f と B_f が名前衝突することはありません。この実現は簡単ですが、コンテストに特化した不自由なコードを書かされるとも言えます。

  2. ファイルを Main.hs にバンドリングする際に A.f を A_f に変換する (例)
    手元では通常のモジュールを使い、バンドリングの際に衝突しない名前に書き換えます。今回はこの方法を実現したいです。

パーサの違い

  • haskell-src-exts
    長らくメンテナンスされておらず、最新の構文に対応していませんが、 { .. } 構文を使ってコードを 1 行にフォーマットする機能があります。

  • ghc-lib-parser
    最終的にはこちらを使いたいです。

要求の段階

  1. qualified imports の利用を名前解決する
    最低限、バンドリングできるようになります。これは手動で頑張ってもなんとかなりそうです。

  2. 個々の関数呼び出しを名前解決する
    不要な関数を提出から削除できるとコンパイル速度で有利です。

制限

以下の制限を設けても実用上は問題無さそうです。

  • モジュール名に対応し 1:1 でファイル名が存在するものとする

haskell-names

ズバり、名前解決のライブラリです。 haskell-src-exts に依存しているのが無念ですが、試す価値がありそうです。

依存のバージョンの衝突

依存関係の矛盾は cabal run --allow-newer で通過できましたが、どうもコンパイルに失敗します。

src/Language/Haskell/Names/Imports.hs:44:7: error:
    Variable not in scope: guard :: Bool -> [a0]
   |
44 |       guard (dropAnn (importModule importDecl) == preludeModuleName)))
   |       ^^^^^

明らかに Control.Monad (guard) が無いせいなんですが、なぜ……？　Fork するしかない。

annotate

annotate 関数が Scoped l の列を返してくれます。

nVertsSG の名前解決結果を見てみます。

Scoped (GlobalSymbol (Selector {symbolModule = ModuleName () "Data.Graph.Sparse", symbolName = Ident () "nVertsSG", typeName = Ident () "SparseGraph", constructors = [Ident () "SparseGraph"]}) (UnQual () (Ident () "nVertsSG"))) (SrcSpanInfo {srcInfoSpan = SrcSpan "src/Data/Graph/Sparse.hs" 418 10 418 18, srcInfoPoints = []}),Scoped None (SrcSpanInfo {srcInfoSpan = SrcSpan "src/Data/Graph/Sparse.hs" 418 19 418 21, srcInfoPoints = []})

フォーマットしてコメントをつけると:

Scoped (
  // 名前解決の結果っぽい
  GlobalSymbol (
    Selector {
      symbolModule = ModuleName () "Data.Graph.Sparse",
      symbolName = Ident () "nVertsSG",
      typeName = Ident () "SparseGraph",
      constructors = [Ident () "SparseGraph"]
    }
  )
  // 元の文字列っぽい
  (UnQual () (Ident () "nVertsSG"))
)
(SrcSpanInfo {
  // 元のソース位置
  srcInfoSpan = SrcSpan "src/Data/Graph/Sparse.hs" 418 10 418 18,
  srcInfoPoints = []}
)

外部パッケージを名前解決するには

今度は U.Vector の名前解決結果を確認します。

Scoped (
  ScopeError (
    EModNotFound (
      ModuleName (
        SrcSpanInfo {
          srcInfoSpan = SrcSpan "src/Data/Graph/Sparse.hs" 23 18 23 29,
	  srcInfoPoints = []
	}
      )
      "Data.Vector"
    )
  )
)
(SrcSpanInfo {
  srcInfoSpan = SrcSpan "src/Data/Graph/Sparse.hs" 23 1 23 34,
  srcInfoPoints = [
    SrcSpan "src/Data/Graph/Sparse.hs" 23 1 23 7,
    SrcSpan "src/Data/Graph/Sparse.hs" 23 8 23 17,
    SrcSpan "src/Data/Graph/Sparse.hs" 23 30 23 32
  ]
})

名前解決に失敗しています。どうも Data.Vector を Environment に追加しておく必要がありそうです。 Prelude に関しては以下のように手動でモジュール名を列挙しています。

-- | Load a basic environment that contains modules very similar to GHC's base package.
loadBase :: IO Environment
loadBase = do
  moduleSymbols <- for baseModules (\moduleName -> do
    dataDir <- getDataDir
    let path = dataDir </> "data" </> "baseEnvironment" </>
          prettyPrint moduleName <.> "symbols"
    symbols <- readSymbols path
    return (moduleName, symbols))
  return (Map.fromList moduleSymbols)

baseModules :: [ModuleName ()]
baseModules = map (ModuleName ()) ["Control.Applicative","Control.Arrow","Control.Category","Control.Concurrent.Chan","Control.Concurrent.MVar","Control.Concurrent.QSem","Control.Concurrent.QSemN","Control.Concurrent","Control.Exception.Base","Control.Exception","Control.Monad.Fix","Control.Monad.Instances","Control.Monad.ST.Imp","Control.Monad.ST.Lazy.Imp","Control.Monad.ST.Lazy.Safe","Control.Monad.ST.Lazy.Unsafe","Control.Monad.ST.Lazy","Control.Monad.ST.Safe","Control.Monad.ST.Strict","Control.Monad.ST.Unsafe","Control.Monad.ST","Control.Monad.Zip","Control.Monad","Data.Bits","Data.Bool","Data.Char","Data.Complex","Data.Data","Data.Dynamic","Data.Either","Data.Eq","Data.Fixed","Data.Foldable","Data.Function","Data.Functor","Data.IORef","Data.Int","Data.Ix","Data.List","Data.Maybe","Data.Monoid","Data.OldTypeable.Internal","Data.OldTypeable","Data.Ord","Data.Ratio","Data.STRef.Lazy","Data.STRef.Strict","Data.STRef","Data.String","Data.Traversable","Data.Tuple","Data.Typeable.Internal","Data.Typeable","Data.Unique","Data.Version","Data.Word","Debug.Trace","Foreign.C.Error","Foreign.C.String","Foreign.C.Types","Foreign.C","Foreign.Concurrent","Foreign.ForeignPtr.Imp","Foreign.ForeignPtr.Safe","Foreign.ForeignPtr.Unsafe","Foreign.ForeignPtr","Foreign.Marshal.Alloc","Foreign.Marshal.Array","Foreign.Marshal.Error","Foreign.Marshal.Pool","Foreign.Marshal.Safe","Foreign.Marshal.Unsafe","Foreign.Marshal.Utils","Foreign.Marshal","Foreign.Ptr","Foreign.Safe","Foreign.StablePtr","Foreign.Storable","Foreign","GHC.Arr","GHC.Base","GHC.Char","GHC.Conc.IO","GHC.Conc.Signal","GHC.Conc.Sync","GHC.Conc","GHC.ConsoleHandler","GHC.Constants","GHC.Desugar","GHC.Enum","GHC.Environment","GHC.Err","GHC.Event.Array","GHC.Event.Clock","GHC.Event.Control","GHC.Event.EPoll","GHC.Event.IntMap","GHC.Event.Internal","GHC.Event.KQueue","GHC.Event.Manager","GHC.Event.PSQ","GHC.Event.Poll","GHC.Event.Thread","GHC.Event.TimerManager","GHC.Event.Unique","GHC.Event","GHC.Exception","GHC.Exts","GHC.Fingerprint.Type","GHC.Fingerprint","GHC.Float.ConversionUtils","GHC.Float.RealFracMethods","GHC.Float","GHC.Foreign","GHC.ForeignPtr","GHC.GHCi","GHC.Generics","GHC.IO.Buffer","GHC.IO.BufferedIO","GHC.IO.Device","GHC.IO.Encoding.CodePage","GHC.IO.Encoding.Failure","GHC.IO.Encoding.Iconv","GHC.IO.Encoding.Latin1","GHC.IO.Encoding.Types","GHC.IO.Encoding.UTF16","GHC.IO.Encoding.UTF32","GHC.IO.Encoding.UTF8","GHC.IO.Encoding","GHC.IO.Exception","GHC.IO.FD","GHC.IO.Handle.FD","GHC.IO.Handle.Internals","GHC.IO.Handle.Text","GHC.IO.Handle.Types","GHC.IO.Handle","GHC.IO.IOMode","GHC.IO","GHC.IOArray","GHC.IORef","GHC.IP","GHC.Int","GHC.List","GHC.MVar","GHC.Num","GHC.PArr","GHC.Pack","GHC.Profiling","GHC.Ptr","GHC.Read","GHC.Real","GHC.ST","GHC.STRef","GHC.Show","GHC.Stable","GHC.Stack","GHC.Stats","GHC.Storable","GHC.TopHandler","GHC.TypeLits","GHC.Unicode","GHC.Weak","GHC.Word","Numeric","Prelude","System.CPUTime","System.Console.GetOpt","System.Environment.ExecutablePath","System.Environment","System.Exit","System.IO.Error","System.IO.Unsafe","System.IO","System.Info","System.Mem.StableName","System.Mem.Weak","System.Mem","System.Posix.Internals","System.Posix.Types","System.Timeout","Text.ParserCombinators.ReadP","Text.ParserCombinators.ReadPrec","Text.Printf","Text.Read.Lex","Text.Read","Text.Show.Functions","Text.Show","Unsafe.Coerce","GHC.CString","GHC.Classes","GHC.Debug","GHC.IntWord64","GHC.Magic","GHC.Prim","GHC.PrimopWrappers","GHC.Tuple","GHC.Types","GHC.Integer.Logarithms.Internals","GHC.Integer.Logarithms","GHC.Integer.Simple.Internals","GHC.Integer.Type","GHC.Integer"]

肝心の readSymbols 関数は、リポジトリ内の *.symbols 関数を読み込んで名前解決しています。 .symbols ファイルを元に名前解決するようです。また .symbols ファイルは resolve 関数により生成できるようです。

よって依存パッケージを動的に resolve するか、 AtCoder ジャッジ環境のパッケージを事前に resolve して .symbols ファイルに変換しておけば良さそうです。

qualified import の名前解決

もう 1 つ試してみます。

import qualified Data.List as L

main :: IO ()
main = do
  let xs = [2, 1, 3]
  print $ L.sort xs

import qualified Data.List as L は長大な名前解決に展開されています。

Scoped (
  Import (
    fromList [
      (Qual () (ModuleName () "L") (Ident () "all"),
        [Value {symbolModule = ModuleName () "GHC.List", symbolName = Ident () "all"}]
      ),
      (Qual () (ModuleName () "L") (Ident () "and"),
      // 省略

L.sort の部分は見事に名前解決されています:

Scoped (
  GlobalSymbol (
    Value {
      symbolModule = ModuleName () "Data.List",
      symbolName = Ident () "sort"
    }
  )
  (Qual () (ModuleName () "L") (Ident () "sort"))
)
(SrcSpanInfo {
  srcInfoSpan = SrcSpan "eg.hs" 6 11 6 17,
  srcInfoPoints = []
})

自作ライブラリを参照 (import とその他) するスパンを元ソースから置換していくことで bundling できそうです。

haskell-names は正しく re-exports を正しく扱えるか

WIP

toyboot4etoyboot4e

[TODO] ghc-lib-parser でコード最小化

やはり haskell-src-exts は更新されていないデメリットがあります。最終的には ghc-lib-parser においてコード最小化 (1 行フォーマット) を実施したいです。

toyboot4etoyboot4e

[TODO] 簡易版 名前解決して埋め込む

haskell-names で真っ当に名前解決するのが大変そうなので、簡易名前解決のスクリプトを考えてます。

  • Main.hs から特定の import を埋め込みに置換する
  • Main.hs と埋め込まれたモジュールでの Module.item を置換する
toyboot4etoyboot4e

[TODO] Top tree

Link/cut tree が概ね実装できたので、 top tree にも手を出して行きましょう。

toyboot4etoyboot4e

(高度) 典型で解けるやつメモ

今後の投稿のネタに

  • ABC 375 A
    TODO: LCP Array で解く
  • TODO
    もっと suffox array ネタ
  • TODO
    Mo で解ける区間和クエリ
  • TODO
    平方分割で解ける何らか
  • TODO
    重みつきUF
  • TODO
    Wavelet Matrix
  • TODO
    最大流
  • TODO
    区間をセットで管理するテクニック
  • TODO
    列を管理する平衡木
toyboot4etoyboot4e

今さら MinHeap

ACL の写経で必要なため、再度実装しました。 Extract (delete, pop) 処理でルートを下へ降りていく際に、より小さい値を持つノードを選んで入れ替えを実施するのが重要です。例: 左右の子が 5, 10 という値であれば、 10 を上に上げると min heap の invariant が崩れます。

https://en.m.wikipedia.org/wiki/Binary_heap

toyboot4etoyboot4e

[DONE] 高速な SCC (Tarjan): O(V + E)

ac-library の SCC を理解します。

原文

R. Tarjan, Depth-First Search and Linear Graph Algorithms

良さそうですが内容が重めです。じっくり読むか……。

Wikipedia

やはり Wikipedia のアルゴリズムは説明の質が高い！

https://en.wikipedia.org/wiki/Tarjan's_strongly_connected_components_algorithm#The_algorithm_in_pseudocode

  • Each node v is assigned a unique integer v.index, which numbers the nodes consecutively in the order in which they are discovered.
    → ord
  • It also maintains a value v.lowlink that represents the smallest index of any node on the stack known to be reachable from v through v's DFS subtree, including v itself.
    → low

Low-link の書き込みの際は、訪問先頂点の隣接頂点 vをすべて見て、それらの low-link の min を取ります。 Low-link の値が未定の頂点は未訪問の頂点ですから DFS を実施し、その low-link を v の low-link に畳み込みます。

Therefore v must be left on the stack if v.lowlink < v.index, whereas v must be removed as the root of a strongly connected component if v.lowlink == v.index.

参考

偉大な先人

https://qiita.com/AkariLuminous/items/a2c789cebdd098dcb503

Verify

Strongly Connected Components - Library Checker

なぜ最後に SCC ID を反転するのか？

SCC が逆トポロジカル順 (下流 → 上流) になっているのをトポロジカル順 (上流 → 下流) にするため