はじめに
母平均の検定、個人的に仮説検定めっちゃ苦手です。というのも、なんか整理しきれてないんですよね。大学院で統計を専門でやっているのに恥ずかしい話ですが、私ですら苦手なので多くの人が苦手意識を持っているのではないでしょうか。なので今回は、苦手な人にも分かりやすいように解説していくので見ていってください。
ちなみに仮説検定は, 帰無仮説 H と対立仮説 K として
片側検定
\begin{align*}
(1) & \ H: \theta = \theta_0, \ K: \theta > \theta_0; &
(1') & \ H: \theta = \theta_0, \ K: \theta < \theta_0; \\
(2) & \ H: \theta \leq \theta_0, \ K: \theta > \theta_0; &
(2') & \ H: \theta \geq \theta_0, \ K: \theta < \theta_0; \\
\end{align*}
と両側検定
(3) \ H: \theta = \theta_0, \ K: \theta \neq \theta_0
があります。
(2),(2’)は(1),(1’)と同様の棄却域を考えれば良いです。(3)は(1)と(1’)を合わせた棄却域を考えれば良いです。
ロードマップ
最速で理解したい人はこの図を暗記してください。笑
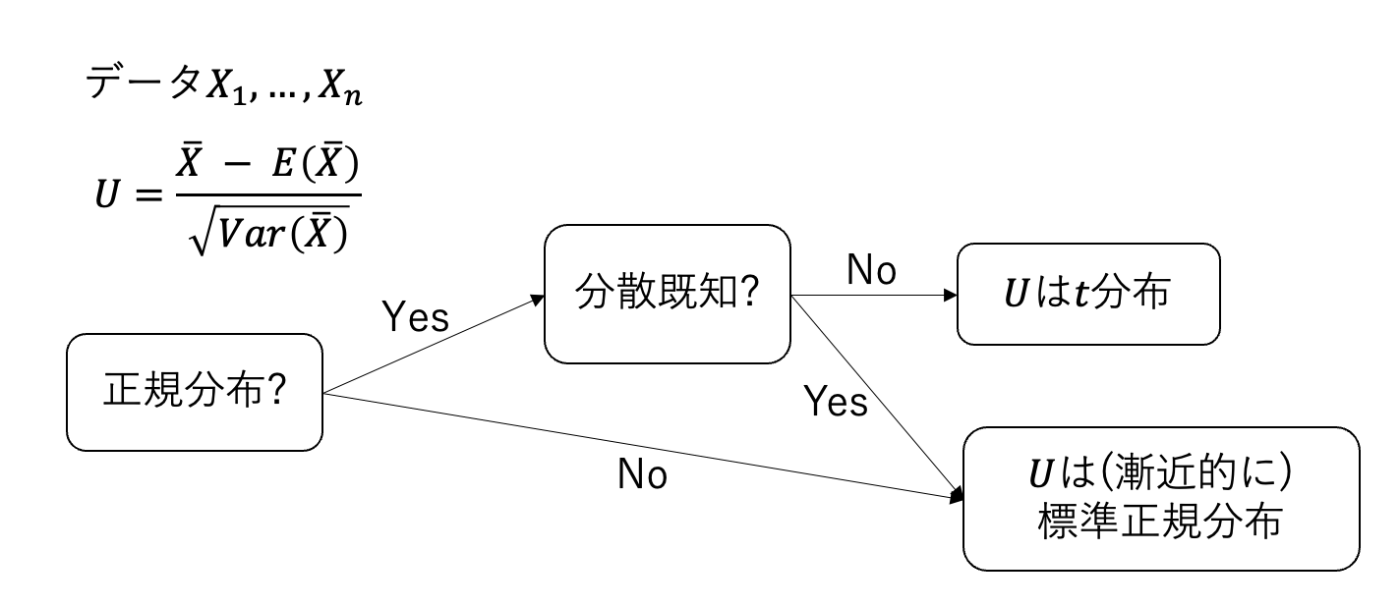
平均\mu ,分散\sigma^2をもつなんらかの分布からデータが得られるとする。
まず、母平均の検定には2つの場合がある。
正規分布かどうか、分散が既知かどうか
ここが大きな違いです。
これらの場合について詳しく見ていきます。
母平均の仮説検定
(1)のパターンを見ていく。
H:\mu=\mu_0 , \ K:\mu > \mu_0
の水準\alphaの問題を考える。平均\mu,分散\sigma^2の分布からのn個のデータをX_1,\dots ,X_nとする。
まず、Hのもとで考える。つまり母平均\mu が\mu_0であると仮定する。
標本平均\bar X = n^{-1}\sum_{i=1}^nX_i は不偏性を持つのでE(\bar X)=\muであることに注意。
このとき\bar Xの期待値と分散は, E(\bar X) =\mu_0 ,
分散が既知の場合は Var(\bar X )=\sigma^2/n
分散が未知の場合は不偏推定量S_0^2 = \sum_{i=1}^n(X_i - \bar X)^2/(n-1)を\sigma^2の代わりに用いてVar(\bar X )=S_{0}^2/n。
統計量Uを次のように定義する。
U = \frac{\bar X - E(\bar X)}{\sqrt{Var(\bar X)}}
Uが何の分布に従うかを考える。
正規分布のとき
1. 分散 \sigma^2 が既知の場合
\begin{equation}
U = \frac{\sqrt{n}(\bar X - \mu_0)}{\sigma}
\end{equation}
U はデータが正規分布から取られているためそのまま標準正規分布に従う。
対立仮説 K:\mu > \mu_0であるため有意水準\alpha とすると棄却域を(a,\infty)としたとき
\begin{equation}
\alpha = P\{\bar X > a \} = P\{U > \sqrt{n}(a - \mu_0)/\sigma\}
\end{equation}
を考えれば良い。\alpha はユーザーが決める。例えば、0.05や0.01がよく用いられる。これよりa がもとまる。
(2)式の式変形はどうなってるかというと
\begin{align*}
P\{\bar X>a\} = P\{(\bar X - \mu_0)/\sigma > (a - \mu_0)/\sigma\} = P\{\sqrt{n}(\bar X - \mu_0)/\sigma > \sqrt{n}(a - \mu_0)/\sigma\}
\end{align*}
N(0,1)の上側100\alpha%点 : u_\alpha,
\begin{equation}
P\{Z > u_\alpha\}=\alpha
\end{equation}
(2)
u_\alpha = \sqrt{n}(a - \mu_0)/\sigma
を計算すれば良いことがわかる。結果は、
a= \mu_0 + u_\alpha(\sigma / \sqrt n)
したがって
\begin{align*}
\bar x > \mu_0 + u_\alpha(\sigma/\sqrt n) \Rightarrow H\text{を棄却}\\
\bar x \leq \mu_0 + u_\alpha(\sigma/\sqrt n) \Rightarrow H\text{を受容}
\end{align*}
検出力を求める。対立仮説K:\mu > \mu_0のもとで棄却域に入る確率を考えれば良い。
\begin{align*}
\gamma(\mu) &=
P\left(\bar X > \mu_0 + u_\alpha \frac{\sigma}{\sqrt n}\right)\\ &= P\left(\bar X - \mu > \mu_0 - \mu + u_\alpha \frac{\sigma}{\sqrt n}\right)\\
&= P\left(\frac{\sqrt{n}(\bar X - \mu)}{\sigma} > \frac{\sqrt{n}( \mu_0 - \mu)}{\sigma} + u_\alpha \right)\\
&=\Phi\left( -
\frac{\sqrt{n}( \mu_0 - \mu)}{\sigma} - u_\alpha
\right)
\end{align*}
ただし\PhiはN(0,1)のc.d.f.とする。
2. 分散 \sigma^2 が未知の場合
分散が未知だから不偏推定量S_0^2で\sigma^2を置き換える。
これらを用いて統計量Uは次のようになる。
\begin{equation}
U = \frac{\sqrt n(\bar X - \mu_0)}{S_0}
\end{equation}
Uは自由度n-1のτ分布に従う。標準正規分布ではなくt分布になることに注意。←ここは暗記して!
対立仮説 K:\mu > \mu_0であるため有意水準\alpha とすると棄却域を(a,\infty)としたとき
t_{n-1}分布の上側100\alpha%点 : t_{\alpha}(n-1)
データから(4)の値t^*を計算して
\begin{align*}
t^* > t_\alpha(n-1) \Rightarrow H\text{を棄却}\\
t^* \leq t_\alpha(n-1) \Rightarrow H\text{を受容}
\end{align*}
次に検出力を求める。対立仮説K:\mu > \mu_0のもとで棄却域に入る確率を考えれば良い。
\begin{align*}
\gamma(\mu) &= P(U > t_\alpha(n-1))\\
&= P\left(\frac{\sqrt{n} (\bar X - \mu_0)}{S_0} > t_\alpha(n-1) \right)\\
&= P\left(\frac{\sqrt{n} (\bar X - \mu)}{S_0} > t_\alpha(n-1) + \frac{\sqrt{n} (\mu_0 - \mu)}{S_0} \right)\\
&= G_{n-1} \left( - t_\alpha(n-1) - \frac{\sqrt{n} (\mu_0 - \mu)}{S_0} \right)
\end{align*}
ただし、t_{n-1}分布のc.d.f.をG_{n-1}とする。
正規分布以外のとき
データの取られ方が正規分布以外の時のUは(1)または(4)と同様に定義できる。なぜなら中心極限定理よりnが大きい時、漸近的にUは標準正規分布に従う。
分散が未知でも正規分布以外の時はt分布ではなく標準正規分布で近似することに注意。
Uを用いて正規分布の分散既知の場合と同様に棄却域を求めれば良い。
まとめ
何だかややこしいですが、分布が正規分布で分散未知だったらt分布。それ以外は標準正規分布と覚えておきましょう。
t分布も漸近的には正規分布で近似できるので、大雑把にやってしまえば全て標準正規分布で近似して棄却域を求めてるみたいなもんですね。実際大雑把にやるのはダメなのでt分布を用いるのですが、、、
参考文献

Discussion