🟠

主成分分析(PCA)-理論とPythonで実装

2023/10/22に公開

Python

はじめに

今回扱う主成分分析(Principal component analysis ; PCA)は、次元削減の有名な方法である。

pを次元数、nをデータ数とすると $p \le n$ の状況を扱う。

はじめに理論を説明し、次にpythonで実装する。

主成分分析

平均 $\mu$ , 共分散行列 $\Sigma$ をもつ母集団からn個のp次データベクトル $x_j$ , j=1,…,nを無作為に抽出する。そして、共分散行列 $\Sigma$ は以下のように固有値分解できる。

\Sigma=H\Lambda H^T = \sum_{s=1}^p\lambda_{(s)}h_{(s)}h_{(s)}^T

$\Lambda=diag(\lambda_{(1)},...,\lambda_{(p)})$ , $\lambda_{(1)} \ge \cdots \ge \lambda_{(p)}$ ,適当な直交行列 $H=(h_{(1)},...,h_{(d)})$

データ行列 $X\in\R^{n\times p}$ が与えられた時、標本共分散行列Sは

S=\frac{1}{n-1}(X-\bar X)^T(X-\bar X)

Sの固有値分解は

S=\hat H\hat \Lambda\hat H^T = \sum_{s=1}^p\hat\lambda_{(s)}\hat h_{(s)}\hat h_{(s)}^T

$\hat\Lambda=diag(\hat\lambda_{(1)},...,\hat\lambda_{(p)})$ , $\hat\lambda_{(1)} \ge \cdots \ge \hat\lambda_{(p)}$ ,適当な直交行列 $\hat H=(\hat h_{(1)},...,\hat h_{(d)})$

$\hat \lambda_{(s)}$ を第s固有値、 $\hat h_{(s)}$ を第s固有ベクトルという。

この固有値、固有ベクトルを用いて次元を削減する。

どうやって削減するかというと、例えば2次元に削減するのであれば、
$\hat h_{(1)}, \hat h_{(2)}$ を用いて、データXを主成分方向に正射映すれば良い。

データを主成分方向に正射影した座標のことを主成分スコアと言う。

データ $x_j$ の第s主成分スコアは

s_{j(s)}=(x_j - \mu)^T h_{(s)}

である。

実際使う際は母平均はわからないので、標本主成分スコアを用いる。

\hat s_{j(s)} = (x_j -\bar x_n )^T \hat h_{(s)})

寄与率を次のように定義する。

\frac{\hat \lambda_{(s)}}{\sum_{s=1}^p\hat \lambda_{(s)}}

この割合を見ればどのくらいの情報が集約されているかわかる。

Pythonで実装

PCAのフルスクラッチ

import numpy as np

def pca(X, k):
    # 1. データの中心化
    mean = np.mean(X, axis=0)
    X_centered = X - mean

    # 2. 共分散行列を計算
    S = np.cov(X_centered, rowvar=False)

    # 3. 固有値と固有ベクトルを計算
    lam, h = np.linalg.eigh(S)

    # 4. 固有値を降順にソートし、対応する固有ベクトルも並べ替える
    index = np.argsort(lam)[::-1]
    sorted_lam = lam[index]
    sorted_h = h[:, index]

    # 5. 最も大きいk個の固有ベクトルを選ぶ
    selected_h = sorted_h[:, :k]
    
    # データを低次元空間に射影
    X_pca = X_centered @ selected_h
    
    return X_pca

実際、下記の方法で一瞬でPCAできてしまいます笑

sklearnによるPCA

from sklearn.decomposition import PCA
import numpy as np

X # データ
k #抽出する主成分の数

# PCAインスタンスを作成 
pca = PCA(n_components=k)

# PCAモデルにデータをフィット
pca.fit(X)

# データを低次元に変換
X_pca = pca.transform(X)

print(X_pca)

Xとkに必要な値を入れれば終わりです。

おまけ

寄与率と累積寄与率のグラフを作成する。

pca =PCA()
pca.fit(x)

evr=pca.explained_variance_ratio_ #寄与率
cev=np.cumsum(evr) #累積寄与率

# 寄与率のプロット
plt.bar(range(1, len(evr) + 1), evr, alpha=0.5, align='center', label='寄与率')
# 累積寄与率のプロット
plt.step(range(1, len(cev) + 1), cev, where='mid', label='累積寄与率')

plt.xlabel("主成分")
plt.ylabel("寄与率")
plt.legend(loc='best')
plt.tight_layout()
plt.show()

例題

sklearnのwineのデータを2次元に射影して散布図を出力してみる。

まず必要なライブラリをインポートする。

!pip install japanize-matplotlib #日本語で出力するために必要

from sklearn.decomposition import PCA
import numpy as np
import pandas as pd
from sklearn import datasets
import matplotlib.pyplot as plt
%matplotlib inline
import japanize_matplotlib

#データ
wine_data = datasets.load_wine()
x = pd.DataFrame(wine_data.data, columns=wine_data.feature_names)
y = wine_data.target

# PCAインスタンスを作成
pca = PCA(n_components=2)

# PCAモデルにデータをフィットし、低次元に変換
wine_pca = pca.fit_transform(x)

plt.figure(figsize=(10, 7))
for color, i, target_name in zip(['red', 'green', 'blue'], [0, 1, 2], wine_data.target_names):
    plt.scatter(wine_pca[y == i, 0], wine_pca[y == i, 1], color=color, label=target_name)
plt.xlabel('第1主成分')
plt.ylabel('第2主成分')
plt.legend()
plt.show()

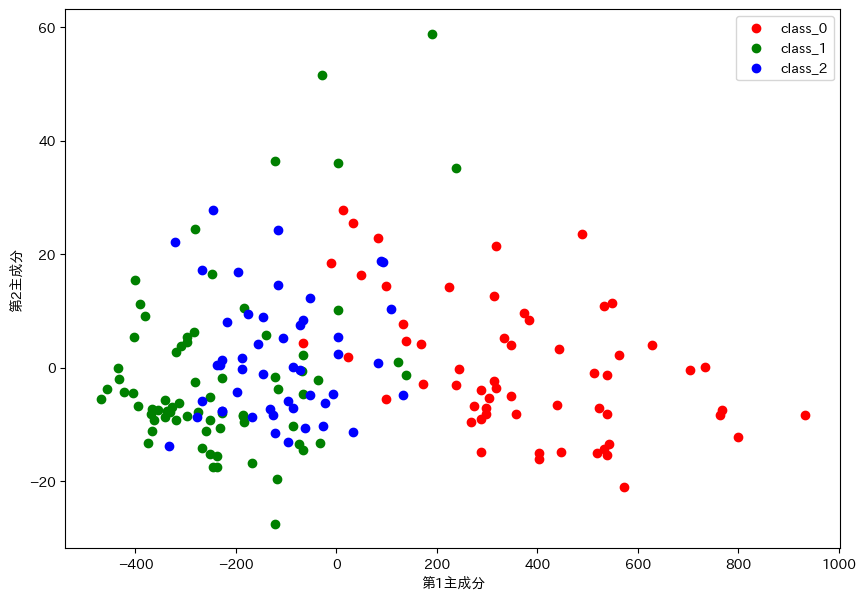
2次元に射影したら流石に分類はできなそうですね。それでもクラス0はその他のクラス（1と2）と分類できそうですね。

でも寄与率見てみたら、第一主成分が99%なのでほぼほぼ情報は保ったまま次元削減できているみたいです。

まとめ

固有値と固有ベクトルを理解するのはかなり苦労するかもしれませんが、PCAをとりあえず実装してみて、情報を集約してるんだなって感じていただければ、理解が一歩進むかもしれないのでやってみてください。