Zenn
🟠

球面集中現象の可視化

2023/11/11に公開
Python
math
#
統計
#
統計学
#
データサイエンス
tech

はじめに

高次元の統計学の2.1節、高次元データベクトルの幾何学的表現について説明します。
https://www.kyoritsu-pub.co.jp/book/b10003167.html
Peter Hall,J. S. Marron,Amnon Neeman (2005) の論文の2節の図2も作成します。

まず読む前に高次元データについて知りたい方はこちらをチェック
https://zenn.dev/totopironote/articles/f13fe705f52d42

高次元データベクトルの幾何学的表現(球面集中現象)

\bm x \sim N_d(0, I_d)とする。d \to \infty のとき、次が成り立つ。

\| \bm x \| = \sqrt{d} + O_p(1) \tag{1}

\bm x_1,\bm x_2 \hspace{3pt} i.i.d. \hspace{3pt}N_d(0, I_d) とする。d \to \infty のとき、次が成り立つ。

\|\bm x_1 -\bm x_2 \| = \sqrt{2d} + O_p(1) \tag{2}
\text{Angle}(\bm x_1,\bm x_2) ≡\cos^{-1} \left( \frac{|\bm x_1^T \bm x_2|}{\|\bm x_1 \| \| \bm x_2 \|} \right) = \frac{\pi}{2} + O_p(d^{-1/2}) \tag{3}

証明

(1)の証明

\bm x=(x_1,…,x_d)^T とする。このとき

\|\bm x \| = \left( \sum_{k=1}^{d} x_k^2 \right)^{1/2}

ここでx_k \sim N(0,1) なので\sum_{k=1}^dx_k^2 \sim \chi_d^2 となる。

\|\bm x\|^2は自由度dのカイ二乗分布に従うのでE(\|\bm x\|^2)=d , Var(\|x\|^2)=2dがわかる。

チェビシェフの不等式を用いて評価する。(大数の法則や中心極限定理使ってもいいです)

チェビシェフの不等式の定義：

P(|X - E(X)| \geq k\sqrt{Var(X)}) \leq \frac{1}{k^2}

ここで、k = d^{\alpha} （ 0 < \alpha < 0.5 ）を選ぶと、不等式は次のようになる：

P\left(\left|\|\bm x \|^2 - d\right| \geq d^{\alpha}\sqrt{2d}\right) \leq \frac{1}{d^{2\alpha}}\to0 \quad(d\to \infty)

よって

\|\bm x\| = \sqrt d + O_p(1) \quad(d\to\infty)

これにより、d が無限に大きくなると、ほぼすべての x が半径 \sqrt{d} の球面上に集中することがわかる。

(2)の証明

\| \bm x_1 - \bm x_2 \|^2 = \sum_{i=1}^{d} (x_{1i} - x_{2i})^2

ここで x_{1i} - x_{2i}\sim N(0,2) （独立した二つの正規分布変数の差の分散は、各分散の和になるため）。 \| \bm x_1 - \bm x_2 \|^2 \sim \chi_d^2 ,E(\|\bm x_1-\bm x_2\|^2)=2d,Var(\|\bm x_1-\bm x_2\|^2)=4d となる。

(1)と同様にして

\|\bm x_1-\bm x_2\|=\sqrt{2d}+O_p(1)\quad (d\to\infty)

となる。

Pythonコード

まず必要なライブラリをインポートする。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA

次にグラフを出力する関数を定義する。標本は3つ。繰り返し回数は100回にしています。

def normal_plot(dim, lims, n=3, ite=100):
    fig, axes = plt.subplots(2, 2, figsize=(10, 10))
    axes = axes.flatten()

    colors = ['red', 'blue', 'green']

    for idx, d in enumerate(dim):
        for _ in range(ite):
            
            generator = np.random.default_rng()
            data = generator.normal(size=(n,d))
            
            pca = PCA(n_components=2)
            data_transformed = pca.fit_transform(data)
            
            #散布図
            for i in range(n):
                axes[idx].scatter(data_transformed[i, 0], data_transformed[i, 1], 
                                  c=colors[i], marker='o')
        
        axes[idx].set_title(f"d={d}")
        axes[idx].grid(True)
        axes[idx].set_xlim(lims[idx])
        axes[idx].set_ylim(lims[idx])

    # Adjust layout to prevent overlap
    plt.tight_layout()
    plt.show()

最後に出力する。

dim = [2, 20, 200, 20000]
lims = [(-3, 3), (-5, 5), (-15, 15), (-150, 150)]
normal_plot(dim, lims)

次元によって軸の値も変えてあげる必要があることに注意

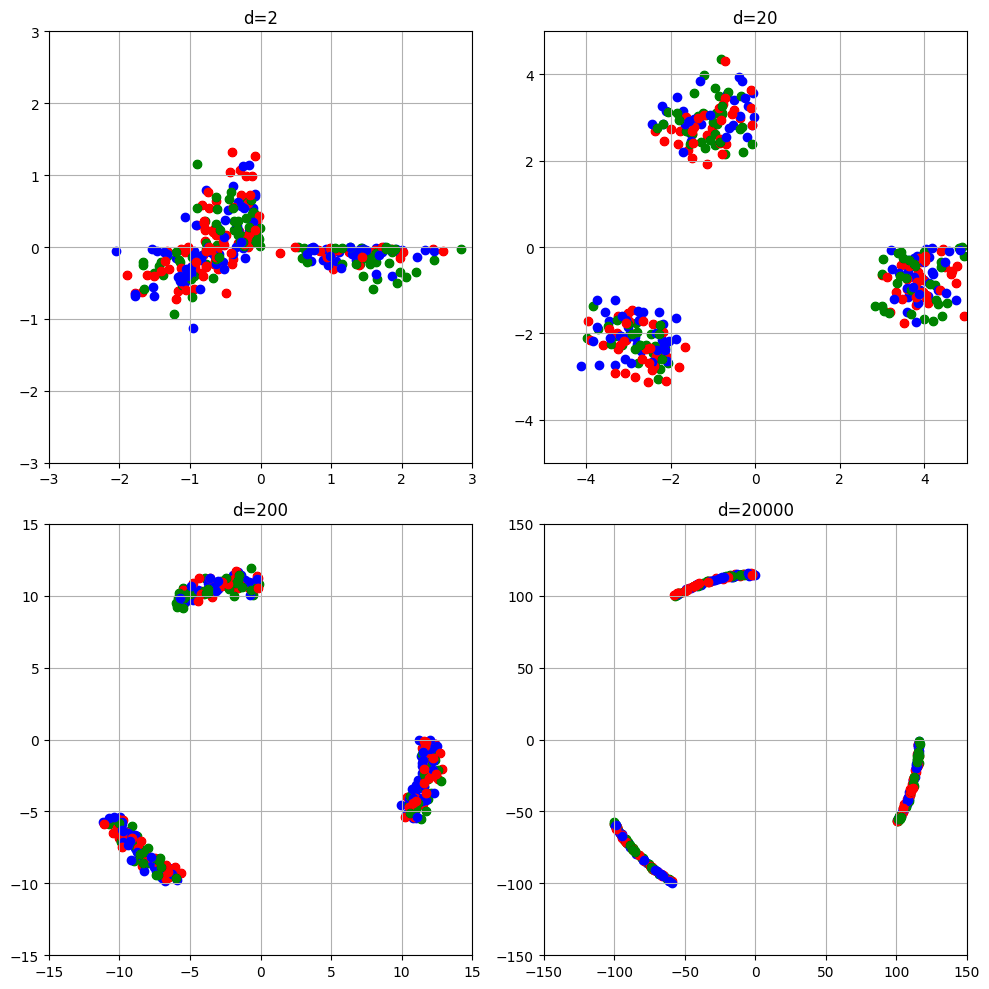
Peter Hall,J. S. Marron,Amnon Neeman (2005)の図2みたいに完全には集まらず、少し幅を持ってしまうのはなぜですかね。

参考文献

Discussion