GPU命令レベルで読むマンデルブロー集合 ~Nsight ComputeとSASS解説~
はじめに
- 目的1:FMA,ALU,SFU(XU)をオーバーラップさせて遊びたい
- 目的2:Nsight Computeのみかたを勉強したい
- 使用したGPU:RTX2080Ti (RTX 3090,RTX 4090,RTX 5090とかも使いたい)
- マンデルブロー集合の計算が簡易アルゴリズムかつコンパイラによる演算の集約が効きにくいので採用
計算内容
マンデルブロー集合は以下の再帰式で定義されます:
この式をとにかくループで計算をすすめて、発散するまでにかかった反復回数をうまいこと表示するとあのきれいな模様がうまれます。
この部分をGPU(NVIDIAのGPU)で計算させます。
このコードはFMA命令に換算すると何命令分?
問題1
// マンデルブロー1ステップ
__device__ __forceinline__ float2 mandelbrot_step(float2 z) {
const float2 c = { -0.7f, 0.27015f };
// z := (x^2 - y^2, 2xy) + c
return make_float2(
z.x * z.x - z.y * z.y + c.x,
2.0f * z.x * z.y + c.y
);
}
RTX 2080Tiで実行するので
nvcc -O3 -arch=sm_75 a.cu -o a.exe
でコンパイル。SASSを見るためNsight Computeでプロファイルしました。

FMUL R5, R7, R7
// R5 = z.y * z.y
FADD R4, R6, R6
// R4 = 2.0 * z.y(後の2xy用)
FFMA R5, R6, R6, -R5
// R5 = z.x * z.x - z.y * z.y(実部の中間計算)
FFMA R4, R7, R4, 0.27015000581741333008
// R4 = z.x * 2.0 * z.y + c.y
FADD R5, R5, -0.69999998807907104492
// R5 = z.x * z.x - z.y * z.y + c.x(c.x = -0.7)
1stepが5命令となりました。(FMA2,ADD2,MUL1)
問題2
// マンデルブロー1ステップ
__device__ __forceinline__ float2 mandelbrot_step(float2 z) {
const float2 c = { -0.7f, 0.27015f };
// z := (x^2 - y^2, 2xy) + c
return make_float2(
z.x * z.x - (z.y * z.y - c.x),
2.0f * z.x * z.y + c.y
);
}
変わったところというと(z.y * z.y - c.x)の部分をカッコでくくっただけです。

FADD R7, R5, R5
// R7 = z.x + z.x (虚部の2.0f * x)
FFMA R6, R4, R4, 0.69999998807907104492
// R6 = z.y * z.y - c.x
FFMA R7, R4, R7, 0.27015000581741333008
// R7 = (2.0f * z.x) * z.y + c.y
FFMA R6, R5, R5, -R6
// R6 =z.x * z.x - (z.y * z.y - c.x)
1stepが4命令となりました。(FMA3,ADD1)
演算律速になっている?→なってた
🔧 プロファイル設定と前提条件
- スレッド数:
THREADS = 1024 - ブロック数:
BLOCKS = 1024 - 各スレッドが
iter = 500回mandelbrot_step() * 8回を実行
📐 総演算量の計算
まず、全体で何回マンデルブローstepが行われたか
🚀 GPUの理論性能の計算
RTX 2080 Ti の仕様:
- SM数: 68
- 1SMあたりの FP32ユニット数: 64
- GPUの動作クロック: 約 1.35 GHz
FP32ひとつが1cycleで1FMA相当のスループットなので、4FMA相当のマンデルブロー1stepを1秒に何回計算できるか?
したがって4194304000 stepにかかる時間は
約 2.856 ms です。
📏 実測時間との比較
- Nsight Computeによる実測:約 3.05 ms
- 理論律速値:約 2.86 ms
これは ほぼ一致しており、明確に演算(FMA)律速であるといえます。

Estimated Speedupが12.49%だけど?
上の画像は1step4命令のときのNsight ComputeのSummaryですが、まだ 12.49 % スピードアップできるかもしれないと書かれています。このキャプチャ画像をChat GPTなどに解析させると "多数のnon-fused命令が検出されており非効率です" みたいなことを言われたりします。しかしそれは 無理 なことがわかります。
- 合計: 393216000 fused FP32命令(例: FMA)
- 合計: 131138560 non-fused FP32命令(例: 単独の ADD, MUL)
この数字は約3:1になっています。SASSで1stepがFMA3,ADD1になっていたことからこの131138560 non-fused FP32命令はほぼ全部 マンデルブロー集合の計算に必要なADD であることがわかります。これ以上どう頑張ってもFMAにまとめることはできません。
12.49%という数字がどこからでてきたのかというと、3:1 の 1 をFMAにまとめると0.5になるから
で算出されたことがわかります。だからプロファイラーのEstimated Speedup(FP32 Non-Fused Instructions)を ”まだコードに改良の余地がある” と鵜呑みにしてはいけません。
なお、1step 5cycleかかるほうのコードのEstimated Speedupは29.98 % になっていました。もちろん本当は5cycle→4cycleが限界なので20%のスピードアップしかできません。
✅ 結論
Nsight ComputeのSummaryのEstimated Speedup(FP32 Non-Fused Instructions) が高いからといってコードに改良の余地があるとは限らない。fusedとnon-fusedの比を見ているだけだった。
今回の (z.y * z.y - c.x) のように、人間がカッコで明示的にFMA化を指示する必要があるし、そのためには脳内コンパイラでどんなSASSができるか想定できると良い。
💡 Estimated Speedupは常に「信用できない数字」なわけではありません。
今回のように演算(FMAパイプ)そのものが律速となり、それが構文上の限界である場合には、Nsightの提案は実際には実行不能な理想論になります。一方で、もしボトルネックが L2キャッシュ通信やDRAM待ち などの メモリ帯域やレイテンシ にある場合、Estimated Speedup の値は比較的現実的な指標になります(...宿題)。
したがって、どのリソースが律速しているか によって Estimated Speedup の「意味の重さ」や「鵜呑みにしてよい度合い」は大きく変わってきます。
宿題
- メモリ律速のコードでEstimated Speedupがどう表示されるかも調査したい
- Detail画面の項目もみていきたい
- 1Warpのみ起動させてScoreboard 依存のstall なども追っていきたい
- __sin()などの命令をSFUで計算させながらFMA実行をオーバーラップさせたい
検証に使ったコード
FMA律速カーネルを1SMだけで実行しルーフライングラフを観察する
使用GPU:RTX2080Ti(全68SM)
1SM実行時のRoofline
手順
Nsight Compute → Details → GPU Speed of Light Throughput → GPU Throughput Rooflines
で Roofline グラフを表示できます。
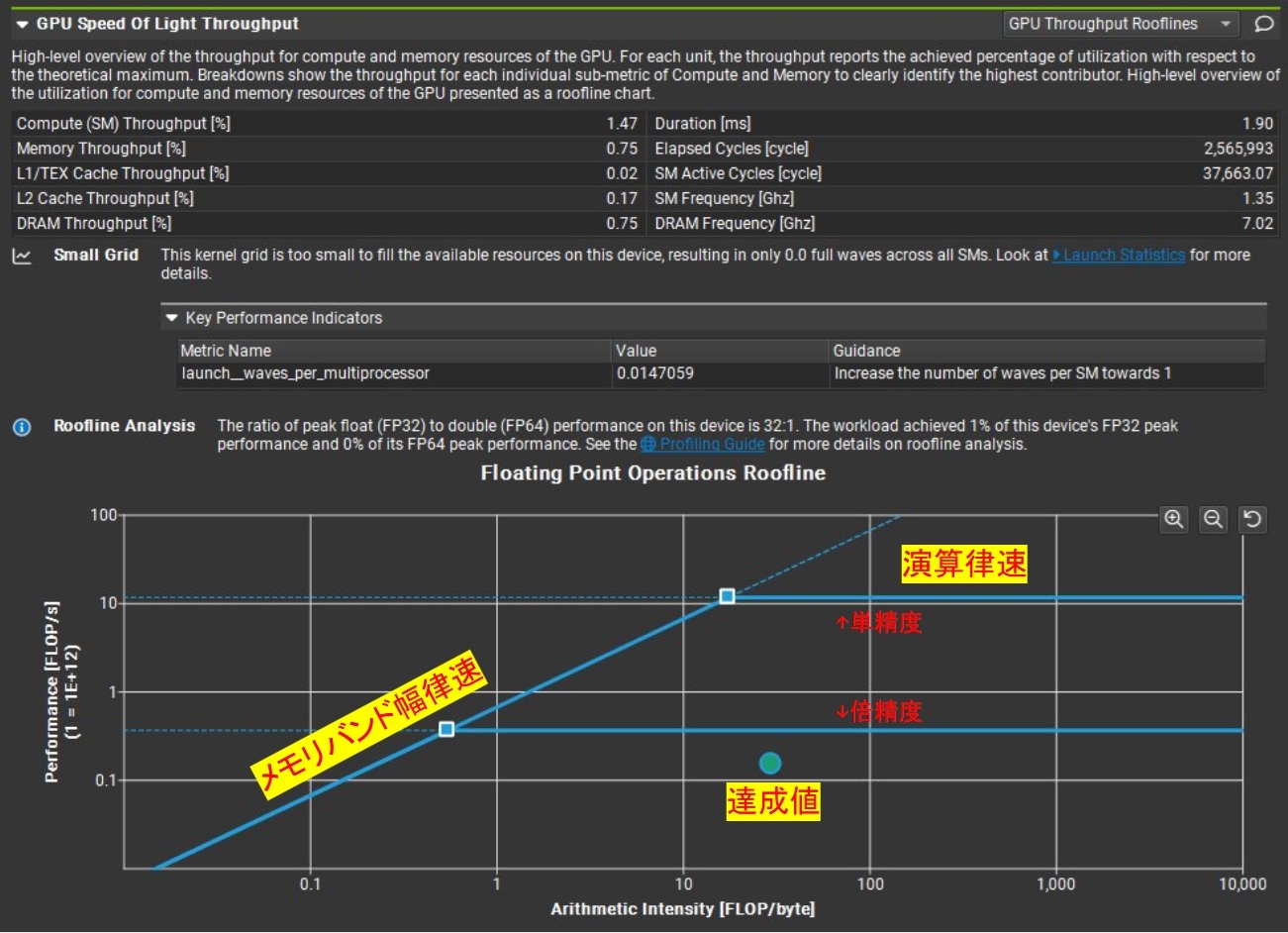
- 斜めの線 … メモリ帯域律速(バンド幅によって性能が決まる領域)
- 水平の線 … 演算律速(演算ユニットのピーク性能で頭打ちになる領域)
- 上段 … 単精度 (FP32) の Roofline
- 下段 … 倍精度 (FP64) の Roofline(今回は無視)
今回は 1 SM だけを有効 にして、わざと
「演算律速のはずなのに GPU が演算ピークに届かない」
という状況を作りました。達成点(緑点)は水平ラインよりかなり下にあります。
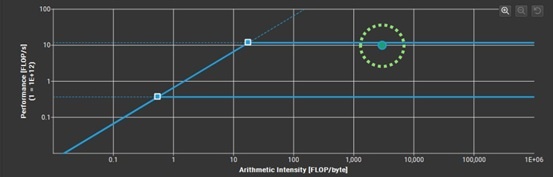
全SM実行時のRoofline
すべての SM を使わせると、達成点はほぼ水平ラインに張り付きます。
Roofline 図の読み方と最適化の指針
| 軸 | 意味 | ポイント |
|---|---|---|
| 横軸 (FLOP/Byte) | 1 FLOP を実行するために何 Byte 転送したか。プログラムで一意に決まるので、横位置は基本的に固定。 | |
| 縦軸 (演算スループット) | 実測の演算性能。高いほど速い。 | 達成点を 上方向にはまだ押し上げられる余地があるかもしれない。 |
例:転送と計算が非オーバーラップなコード
- Global Memory ←→ Register のコピーと演算が 重ならない 場合、
- 転送待ちで SM がアイドル → 達成点は 水平ラインより下 に沈む。
- 転送を
cp.asyncなどで オーバーラップ させられれば、- アイドル時間が減り、達成点は 演算律速ライン に近づく。
例:最適化されてない行列行列積
-
Global Memory ←→ Register のコピーが支配的でメモリバンド幅律速
- 斜めライン に張り付いている状態
- 当然 SM がアイドルな時間も長いがプログラムを完遂するにはメモリ通信をしなければならないのでどうしようもない
-
レジスタブロッキングにかえる
- FLOP/Byteが変わるので達成点が右に移動
- アイドルだったSMが稼働しはじめ達成点が上にも動く
- 水平ライン上に到達すれば 最適化達成
まとめ
見どころは「縦方向」
達成点をさらに上げられるかどうか?──それが最適化余地の有無を示す
ただし横方向へ移動させる手段もたくさんあるのでそのうち記事にしたい
CUDAの__sin()はMUFU.SINとFMULに分解される
SFUとFMAをオーバーラップさせる前に調査
for (uint32_t i = 0; i < iterations; ++i) {
for (int j = 0; j < 8; ++j) {
x = __sinf(x);
}
}
これのSASSをみてみると
FMUL.RZ R9, R5, 0.15915493667125701904
MUFU.SIN R5, R9
FMUL.RZ R10, R5, 0.15915493667125701904
MUFU.SIN R5, R10
FMUL.RZ R11, R5, 0.15915493667125701904
MUFU.SIN R5, R11
この0.15915493667125701904はなにかというと1.0/2πです!
おそらく NVIDIAのSFUにいれる数字はラジアンから0.0~1.0に正規化しておく必要があるようです。(追記:この状態にしておくことで四分円(π/2)区切りのindexとその剰余が簡単に求まるためと思われます)
このコードをNsight Computeで解析すると

うん演算律速!XUはSFUのことを指しています。
画像右のPipe Utilizationをみると、ちゃんとMUFU.SINに対応するXUが100%にはりついて、FMULに対応するFMAが25%になっており想定通りです。
コードと.ncu-repはこちら
なぜ想定通りか
RTX 2080Tiは1つのSMに64個のFP32と16個のSFUを備えています。1SMは4つのSMSPでパーティションで別れており1つのSMSPが1つ以上のwarpをかかえて処理します。
FFMA系命令なら1SMSPが1つのwarpを2cycleかけて処理します。
Turing Tuning Guide 1.4.1.1「Instructions are performed over two cycles…」
SFUは1cycleで1つの超越関数を処理できるのでFP32と超越関数の処理スループット比は4:1になります。なので画像右の100%、25%のグラフは想定通り、XUとFMAがオーバーラップ実行されているっぽいことも読み取れます。
マンデルブロー計算とオーバーラップ
前につくったマンデルブロー1step(=4 cycle)を使ってベンチをしました。
x = __sinf(x); // ①
z = mandelbrot_step(z); // ②
これを1threadあたり4000ループ×(1024*1024thread)で実行
| カーネル | 処理時間(cycles) | 命令比 |
|---|---|---|
| ①__sinf | 4520489 | MUFU1つ+FMUL1つ |
| ②マンデルブロー | 4112138 | FFMA3つ+FADD1つ |
| ①+② | 5405836 | MUFU1つ+FMUL1つ+FFMA3つ+FADD1つ |
もしXUとFMAがオーバーラップしていなければ①+②で時間が2倍になってないとおかしいです。
なおOccupancyは100%で命令レイテンシの隠蔽がちゃんと効く前提となっています。
宿題
- ①+②ではFMA負荷:XU負荷が5:1になって気持ち悪いので4:1になるように調整して再プロファイル
- 1warpだけにして実行したい。SASS上でRAW依存をなるべくなくして100% ALU効率を目指すチャンレンジ
WarpスケジューラーとMUFU.SIN発行8cycle待ちの関係(自信ない)
①+②のような処理内容を、1SMSPで1Warpだけ実行するようにして、命令レベル並列性(ILP)を確保してSASS命令を順にStallなく実行できるよう用意したとします。そうするとFFMA→MUFU.SIN→FFMA→・・・と順次Dispatchされ、適切な命令レンテンシを経た後結果が該当レジスタに入る、それが次の処理に・・とスムーズに行われるはずです。
SFUは1SMSP(32thread)に対し4つしかないのでMUFU.SINは発行に8cycleかかるはずですが、ここで個人的にわからないのは MUFU.SINが発行開始されたcycleの次のcycleでFFMAが発行できるのか?または8cycle待たされるのか? ということです。もし前者なら理論上100%に近いFMAスループットがだせるはずですがどうでしょう。
RTX2080Tiは68SMなのでBlock数は68に、1BlockあたりのThread数は128にして1SMSP1Warpとなるよう調整します。このままでは1SMに2Block割り当てられたりするので1SM1Blockを強制するために意味なく48KBのShared Memoryを確保しています。
計測コードを見る
.cuコード
// sin_mandel_bench.cu
// ------------------------------------------------------------
// 1 SM あたり 1 block だけを常駐させるために、動的共有メモリを
// 64 KiB (= 65 536 B) 消費させる最小構成ベンチマーク
// nvcc -O3 -arch=sm_75 sin_mandel_bench.cu -o sinMandelBench.exe
// ------------------------------------------------------------
#include <cstdio>
#include <cstdlib>
#include <cuda_runtime.h>
// --- ヘルパ --------------------------------------------------
inline void check(cudaError_t err, const char* file, int line)
{
if (err != cudaSuccess) {
std::fprintf(stderr, "CUDA error %s (%d) at %s:%d\n",
cudaGetErrorString(err), int(err), file, line);
std::exit(EXIT_FAILURE);
}
}
#define CUDA_CHECK(e) check((e), __FILE__, __LINE__)
// --- Mandelbrot 1-step --------------------------------------
__device__ __forceinline__ float2 mandelbrot_step(float2 z)
{
const float2 c = { -0.7f, 0.27015f };
return make_float2(
z.x * z.x - (z.y * z.y - c.x),
2.0f * z.x * z.y + c.y
);
}
// --- メインカーネル(Sin+Mandel 混在) ----------------------
__global__ void benchKernel(uint32_t iterations, float* result)
{
extern __shared__ uint8_t smem[]; // 何もしないが 64 KiB 確保用
const uint32_t gid = blockIdx.x * blockDim.x + threadIdx.x;
float x0 = 0.000123f * (gid + 189124);
float x1 = 0.000123f * (gid + 6741);
float x2 = 0.000123f * (gid + 913);
float x3 = 0.000123f * (gid + 1);
float2 z0 = make_float2(0.00010f * (gid / 64), x0);
float2 z1 = make_float2(0.00012f * (gid / 64), x1);
float2 z2 = make_float2(0.00014f * (gid / 64), x2);
float2 z3 = make_float2(0.00017f * (gid / 64), x3);
#pragma unroll
for (uint32_t i = 0; i < iterations; ++i) {
x0 = __sinf(x0); z0 = mandelbrot_step(z0);
x1 = __sinf(x1); z1 = mandelbrot_step(z1);
x2 = __sinf(x2); z2 = mandelbrot_step(z2);
x3 = __sinf(x3); z3 = mandelbrot_step(z3);
}
if (threadIdx.x == 0) {
result[blockIdx.x] =
x0 + x1 + x2 + x3 +
z0.x + z1.x + z2.x + z3.x;
}
}
// --- 起動 ----------------------------------------------------
int main(int argc, char* argv[])
{
if (argc < 2) {
std::printf("Usage: %s <iterations>\n", argv[0]);
return 0;
}
const uint32_t iters = std::atoi(argv[1]);
cudaSetDevice(1);
// 結果バッファ (#block 要素)
constexpr int THREADS = 128;
constexpr int BLOCKS = 68; // RTX 2080 Ti は 68 SM
float* d_result = nullptr;
CUDA_CHECK(cudaMallocManaged(&d_result, sizeof(float) * BLOCKS));
// 動的共有メモリ:1 block あたり 64 KiB (= 65 536 B)
constexpr size_t SHMEM_BYTES = 48 * 1024;
benchKernel<<<BLOCKS, THREADS, SHMEM_BYTES>>>(iters, d_result);
CUDA_CHECK(cudaGetLastError());
CUDA_CHECK(cudaDeviceSynchronize());
// 出力(合計値を簡易的に確認)
double sum = 0.0;
for (int i = 0; i < BLOCKS; ++i) sum += d_result[i];
std::printf("Accumulated result = %.7f\n", sum);
CUDA_CHECK(cudaFree(d_result));
return 0;
}
生成されたSASS
MOV R1, c[0x0][0x28]
S2R R0, SR_CTAID.X
ISETP.NE.AND P0, PT, RZ, c[0x0][0x160], PT
S2R R3, SR_TID.X
IMAD R2, R0, c[0x0][0x0], R3
IADD3 R4, R2, 0x2e2c4, RZ
IADD3 R5, R2, 0x1a55, RZ
IADD3 R8, R2, 0x391, RZ
IADD3 R9, R2, 0x1, RZ
I2F.U32 R4, R4
SHF.R.U32.HI R2, RZ, 0x6, R2
I2F.U32 R5, R5
I2F.U32 R8, R8
FMUL R6, R4, 0.00012300000526010990143
I2F.U32 R9, R9
FMUL R11, R5, 0.00012300000526010990143
I2F.U32 R2, R2
FMUL R14, R8, 0.00012300000526010990143
FMUL R15, R9, 0.00012300000526010990143
FMUL R7, R2, 9.9999997473787516356e-05
FMUL R16, R2, 0.00011999999696854501963
FMUL R13, R2, 0.00014000000373926013708
FMUL R5, R2, 0.0001699999993434175849
@!P0 BRA 0x160264be80
MOV R4, c[0x0][0x160]
MOV R9, R15
IADD3 R2, R4, -0x1, RZ
LOP3.LUT R4, R4, 0x3, RZ, 0xc0, !PT
ISETP.GE.U32.AND P1, PT, R2, 0x3, PT
ISETP.NE.AND P0, PT, R4, RZ, PT
MOV R8, R14
MOV R10, R11
MOV R12, R6
@!P1 BRA 0x160264bca0
IADD3 R2, -R4, c[0x0][0x160], RZ
MOV R9, R15
MOV R8, R14
MOV R10, R11
MOV R12, R6
FMUL.RZ R19, R11, 0.15915493667125701904
IADD3 R2, R2, -0x4, RZ
FMUL.RZ R6, R6, 0.15915493667125701904
FMUL.RZ R17, R14, 0.15915493667125701904
ISETP.NE.AND P1, PT, R2, RZ, PT
FMUL.RZ R20, R15, 0.15915493667125701904
MUFU.SIN R11, R19
FFMA R15, R10, R10, 0.69999998807907104492
FFMA R15, R16, R16, -R15
MUFU.SIN R6, R6
MUFU.SIN R17, R17
FMUL.RZ R18, R11, 0.15915493667125701904
FADD R11, R7, R7
FFMA R11, R11, R12, 0.27015000581741333008
MUFU.SIN R20, R20
FMUL.RZ R14, R6, 0.15915493667125701904
FFMA R12, R12, R12, 0.69999998807907104492
FFMA R6, R8, R8, 0.69999998807907104492
FFMA R12, R7, R7, -R12
MUFU.SIN R18, R18
FMUL.RZ R21, R17, 0.15915493667125701904
FADD R17, R16, R16
FADD R7, R13, R13
FFMA R17, R17, R10, 0.27015000581741333008
MUFU.SIN R14, R14
FMUL.RZ R20, R20, 0.15915493667125701904
FADD R10, R5, R5
FFMA R7, R7, R8, 0.27015000581741333008
FFMA R8, R9, R9, 0.69999998807907104492
MUFU.SIN R19, R21
FMUL.RZ R18, R18, 0.15915493667125701904
FFMA R10, R10, R9, 0.27015000581741333008
FFMA R9, R11, R11, 0.69999998807907104492
FFMA R8, R5, R5, -R8
MUFU.SIN R20, R20
FMUL.RZ R22, R14, 0.15915493667125701904
FADD R14, R12, R12
FFMA R6, R13, R13, -R6
FFMA R14, R11, R14, 0.27015000581741333008
MUFU.SIN R18, R18
FMUL.RZ R19, R19, 0.15915493667125701904
FFMA R11, R10, R10, 0.69999998807907104492
FFMA R9, R12, R12, -R9
FFMA R5, R7, R7, 0.69999998807907104492
MUFU.SIN R19, R19
FMUL.RZ R20, R20, 0.15915493667125701904
FFMA R12, R17, R17, 0.69999998807907104492
FADD R16, R15, R15
FADD R13, R8, R8
MUFU.SIN R20, R20
FFMA R8, R8, R8, -R11
FFMA R5, R6, R6, -R5
FADD R11, R9, R9
FFMA R12, R15, R15, -R12
MUFU.SIN R21, R22
FADD R6, R6, R6
FFMA R16, R17, R16, 0.27015000581741333008
FFMA R13, R10, R13, 0.27015000581741333008
FFMA R10, R14, R11, 0.27015000581741333008
FFMA R7, R7, R6, 0.27015000581741333008
FADD R11, R12, R12
FFMA R6, R14, R14, 0.69999998807907104492
FFMA R15, R16, R16, 0.69999998807907104492
FADD R14, R5, R5
FFMA R17, R16, R11, 0.27015000581741333008
FFMA R15, R12, R12, -R15
FMUL.RZ R22, R18, 0.15915493667125701904
FFMA R12, R7, R7, 0.69999998807907104492
FFMA R18, R7, R14, 0.27015000581741333008
FFMA R7, R13, R13, 0.69999998807907104492
MUFU.SIN R11, R22
FMUL.RZ R23, R19, 0.15915493667125701904
FFMA R14, R10, R10, 0.69999998807907104492
FMUL.RZ R24, R20, 0.15915493667125701904
FFMA R9, R9, R9, -R6
FFMA R16, R17, R17, 0.69999998807907104492
FMUL.RZ R21, R21, 0.15915493667125701904
FFMA R5, R5, R5, -R12
FADD R12, R8, R8
FFMA R19, R8, R8, -R7
MUFU.SIN R6, R21
FFMA R7, R9, R9, -R14
FADD R8, R15, R15
FFMA R16, R15, R15, -R16
FADD R9, R9, R9
MUFU.SIN R14, R23
FFMA R21, R13, R12, 0.27015000581741333008
FFMA R12, R10, R9, 0.27015000581741333008
FFMA R10, R17, R8, 0.27015000581741333008
FFMA R8, R18, R18, 0.69999998807907104492
MUFU.SIN R15, R24
FADD R9, R5, R5
FFMA R20, R21, R21, 0.69999998807907104492
FADD R22, R19, R19
FFMA R13, R5, R5, -R8
FFMA R8, R18, R9, 0.27015000581741333008
FFMA R5, R19, R19, -R20
FFMA R9, R21, R22, 0.27015000581741333008
@P1 BRA 0x160264b670
@!P0 BRA 0x160264be80
FMUL.RZ R6, R6, 0.15915493667125701904
IADD3 R4, R4, -0x1, RZ
FMUL.RZ R11, R11, 0.15915493667125701904
FMUL.RZ R14, R14, 0.15915493667125701904
ISETP.NE.AND P0, PT, R4, RZ, PT
FMUL.RZ R15, R15, 0.15915493667125701904
MUFU.SIN R6, R6
FFMA R2, R12, R12, 0.69999998807907104492
FADD R17, R7, R7
FFMA R7, R7, R7, -R2
FFMA R2, R9, R9, 0.69999998807907104492
MUFU.SIN R11, R11
FFMA R12, R17, R12, 0.27015000581741333008
FFMA R2, R5, R5, -R2
FFMA R21, R10, R10, 0.69999998807907104492
FADD R19, R16, R16
MUFU.SIN R14, R14
FADD R17, R13, R13
FFMA R20, R8, R8, 0.69999998807907104492
FADD R18, R5, R5
MOV R5, R2
FFMA R16, R16, R16, -R21
MUFU.SIN R15, R15
FFMA R10, R19, R10, 0.27015000581741333008
FFMA R13, R13, R13, -R20
FFMA R8, R17, R8, 0.27015000581741333008
FFMA R9, R18, R9, 0.27015000581741333008
@P0 BRA 0x160264bcb0
MOV R5, R2
ISETP.NE.AND P0, PT, R3, RZ, PT
@P0 EXIT
FADD R11, R11, R6
MOV R3, 0x4
FADD R14, R11, R14
IMAD.WIDE.U32 R2, R0, R3, c[0x0][0x168]
FADD R14, R14, R15
FADD R7, R14, R7
FADD R16, R7, R16
FADD R16, R16, R13
FADD R5, R16, R5
STG.E.SYS [R2], R5
EXIT
BRA 0x160264bf50
NOP
NOP
以下のコマンドで実行
nvcc -O3 -arch=sm_75 sincos_bench.cu -o sincosBenchCuda.exe
ncu --set detailed --export SinMandelOverlap.ncu-rep --kernel-name "benchKernel" ./sincosBenchCuda.exe 55000 1
Nsight Computeの結果

考察
SASSをみると __sinf() と mandelbrot_step() に相当するFFMAとMUFU.SINが生成されており、ループ内のセクションに
FFMA系 80個 (FADD, FMUL含む)
MUFU.SIN 16個
あることがわかります。ここまでは計算にあいます。
もし MUFU.SIN が 8 サイクルかかり、その間に同一Warp内で次の命令( FFMA)を発行できない場合、全体FMAのスループットは次のように計算されます:
ここで:
- 80 * 2 :80命令分のFMAが2サイクルで発行される(スループット最大)。
- 16 * 8 :16命令分の
MUFU.SINがそれぞれ8サイクル占有してFMA発行をブロックする時間。
この結果、FMAのスループットは制限され55.5%に落ち込まないといけないですが、プロファイルではそうはなっていません。
なのでWarpの視点からみるとMUFU.SINの1cycle後(または2cycle後?)にFFMAを発行できているのではないか、というのが今の結論です。ここらへんの情報収集にChat GPT o3を使いましたが、o3がいうには8cycleロックされるとのことでした。しかしそれを明らかに超えるスループットが出ているんですよね・・
実行速度から検証
最後にカーネル全体の実行速度からスループットを割り出してみます。
1 thread あたりで実行される FMA の総数は:
1つの FMA を 2 サイクルで処理するので(64*FP32に対し128threadなので)、理論上必要なサイクル数は:
クロック 1.33 GHz で割ると、理論実行時間(100%スループット時)は:
FMAが 55.5% のスループットでしか動作しない場合の実行時間は:
実際の実行時間は:
- 2.06 ms(= 2,784,304 cycles)
よって、速すぎる のです。
やっぱり8cycleロックされないんじゃないかなー
宿題
- FP32とINT32をオーバーラップするコードで検証
- これならFP32とINT32を交互cycleに発行しないとどちらも100%スループットを達成できないはず