CUDA/PTX LOP3命令の解説(使いこなせる人はいるのか?)
LOP3はルックアップテーブル(LUT)を用いて3入力の任意論理演算を実行できる命令
対象:
NVIDIA GPU, CUDA / PTX, ビット演算・最適化に関心のある人
SASSをながめていたらLOP3.LUTがでてきて気になった人
lop3.b32 d, a, b, c, immLut; は 3入力ブール関数 d=F(a,b,c) を 32bit幅の各ビットに独立に適用 し32bitの d を得る PTX 命令です。SASSでは LOP3.LUT として出現します。
immLut は 8bit即値で0~255までを指定できます。ざっくりいうと、入力が(a,b,c)=8通りあって、出力がこの8(通り)*256(パターン)個の0,1で考えられます(下記表)。この256の部分を即値できめることができます。うまく使うと1命令で AND/OR/XOR の合成,sel ? x : y の MUX,Majority,Parity などを実現できます。がそのぶん可読性は低下しがちです。
出典: PTX ISA 8.1, §9.7.7.6 “Logic and Shift Instructions: lop3”, p.182 [https://docs.nvidia.com/cuda/archive/12.1.0/pdf/ptx_isa_8.1.pdf]
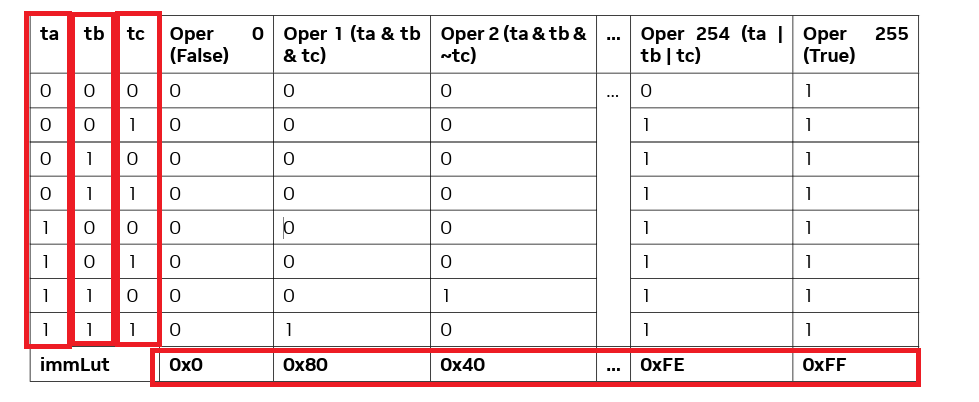
表をみるとわかりやすいと思います。というかこれが全てです!目に焼き付けてください。
赤枠が入力で、即値 immLut の0x0~0xFFに応じて返るbool値の組み合わせが256通りになっています。例えば即値が 0x80 なら ta & tb & tc の計算を意味します。ta,tb,tc は各入力ワードの ある1ビット位置に注目したときの 0/1 です(命令は全32ビットについて同じ1-bit関数を並列に評価します)。
補足:ブール関数とは?
ブール関数とは、0 または 1(真/偽)の入力を受け取り、0 または 1 を返す関数のことです。
例えば2入力で考えると「AND」は両方の入力が 1 のときだけ 1 を返す関数、「OR」はどちらかが 1 なら 1 を返す関数、「NOT」は入力を反転させる関数です。
memo:表の理解を深める
この表の見方
表は一部省略されています。ただ規則性があることがわかります。表の下側を上位bit、表の上側を下位bitとして0,1を並べると即値0x80は10000000、0x40は01000000、0xFEは11111110となっていることがわかります。すなわち即値と表を縦にみたときの01の並びが同じ値になっている可能性が高いです。それしかないでしょう。なので即値0x01なら00000001という並びになっていることが想像できます。
2入力(a,b)で 16パターン になる理由と3入力の場合
n入力ブール関数の総数は 2^(2^n)。2入力なら、入力の組合せは 4 通り(00, 10, 01, 11)。各組合せに対して出力 0/1 を自由に選べるので 2^4 = 16 通りの関数が存在します。
2入力の真理値表おさらい
| a | b | AND (a & b) |
OR (a | b) |
XOR (a ^ b) |
NOR (~(a | b)) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 |
ここではAND OR XOR NORだけを書いていますが、1,0,1,1 のような出力だって作れるはずです。それらを全部あわせれば16パターンになります。
| パターン (f(00) f(10) f(01) f(11)) | 関数名・別名 |
|---|---|
| 0000 | 恒偽 (False) |
| 0001 | AND (a & b) |
| 0010 |
a & ~b (implication形式で "a AND NOT b") |
| 0011 | f = a (恒等写像) |
| 0100 | ~a & b |
| 0101 | f = b |
| 0110 | XOR (a ^ b) |
| 0111 | OR (a | b) |
| 1000 | NOR (~(a | b)) |
| 1001 | XNOR (equivalence) |
| 1010 | NOT b |
| 1011 |
a ⇒ b(含意: if a then b) |
| 1100 | NOT a |
| 1101 |
b ⇒ a(含意: if b then a) |
| 1110 | NAND (~(a & b)) |
| 1111 | 恒真 (True) |
ということで、2入力(a,b)で 16通りの関数 を作ることができました。
この2入力が3入力になったものが上記LOP3の表そのものです。そこでは 256通り の関数が存在するわけです。
immLut の作り方
d = (a & b) | (~a & c)
のような任意式をLOPを使ってプログラミングしたいとします。このとき immLut には何を指定したら良いでしょう?
答えは0xCAになりますが、これは割と簡単に求められます。
A = 0xF0
B = 0xCC
C = 0xAA
immLut = F(A, B, C) をビット演算として評価した値 (下位8bit)
任意の論理式 F(A,B,C) を そのままビット演算で A = 0xF0, B = 0xCC, C = 0xAA に代入して評価すると、得られた 8bit 値が immLut になります。
-
F = (a & b) | (~a & c)→imm = (0xF0 & 0xCC) | (~0xF0 & 0xAA) = 0xCA -
a & b & c→0x80 -
a | b | c→0xFE - 常に1 →
0xFF
余談
「この表の見方」で説明したよう表をしたからながめて上位~下位bitをならべると
A = 0xF0 = 11110000
B = 0xCC = 11001100
C = 0xAA = 10101010
となりta,tb,tcの赤枠でかこった並びと一致してます。即値に0xF0を指定するとaの入力がそのまま返ってくる、という理解が直感的にできます。
よく使う(?)関数の immLut 例
下の即値はすべて
A=0xF0, B=0xCC, C=0xAAを代入して評価して得られる値です。
| 関数 | 式 | immLut |
|---|---|---|
| AND2 | a & b |
0xC0 |
| OR2 | a | b |
0xFC |
| XOR2 |
a ^ b(c未使用) |
0x3C |
| NOT | ~a |
0x0F |
| NAND2 | ~(a & b) |
0x3F |
| NOR3 | ~(a | b | c) |
0x01 |
| OR3 | a | b | c |
0xFE |
| AND3 | a & b & c |
0x80 |
| Parity(3入力 XOR) | a ^ b ^ c |
0x96 |
| Majority(多数決,2/3以上が1で1) | (a&b)|(a&c)|(b&c) |
0xE8 |
MUX(a ? b : c,aがセレクタ) |
(a & b) | (~a & c) |
0xCA |
他にも任意の論理関数を表現できるわけですが、面白い使い道がすぐには思いつきません。ライフゲームとかに使えないだろうか?
もしこういう使い道があるよという例があればぜひ教えて下さい!
CUDAからの使い方(インラインPTX)
__device__ __forceinline__ uint32_t lop3_u32(uint32_t a, uint32_t b, uint32_t c) {
uint32_t d;
asm volatile ("lop3.b32 %0, %1, %2, %3, 0x96;" // ← imm を直接埋め込み
: "=r"(d)
: "r"(a), "r"(b), "r"(c));
return d;
}
実装時の注意
-
アーキ要件:
lop3.b32は SM 5.0 (Maxwell) 以降。-arch=sm_50以上でコンパイル必須 - 即値は コンパイル時定数(
"n"制約)。実行時に可変な LUT は不可 -
2入力関数の場合:
c=0を渡す前提で「cに依存しない形」の即値(例:a|b→0xFC)を使うと分かりやすい -
可読性:難解な即値はコメントで式と由来(
A=0xF0, B=0xCC, C=0xAA)を書いておくと保守しやすい - 速度:LOP3.LUTはINT ALUで処理される。整数演算命令 IADD, IMAD, SHFと同等のスループット・レイテンシ
Discussion