🚀

CUDAの__sinf()はSASSでFMUL → MUFU.SINに展開される

2025/08/28に公開

 SASSをみてみる主要ベンダーGPUには、単精度の sin/cos を高速に近似計算する専用ハードウェア(例：SFU)が備わっています。ここでは NVIDIA RTX 2080 Tiで、CUDA の __sinf() が SASS（GPUアセンブリ）でどのような命令列になるかを調査しました。専用ハードウェア上で実行される命令が出現するはずです。
CUDAコード
for (uint32_t i = 0; i < iterations; ++i) {
            for (int j = 0; j < 8; ++j) {
                x = __sinf(x);
            }
}
これのSASSをみてみると
-----一部抜粋-----
     FMUL.RZ R9, R5, 0.15915493667125701904
     MUFU.SIN R5, R9
     FMUL.RZ R10, R5, 0.15915493667125701904
     MUFU.SIN R5, R10
     FMUL.RZ R11, R5, 0.15915493667125701904
     MUFU.SIN R5, R11
-----------------
ループが展開され、__sinf(x) 1回の呼び出しが「 FMUL 1発 → MUFU.SIN 1発」に対応していることがわかります。MUFU.SIN が専用ハードウェア（SFU）での近似計算に相当します。ここで現れる 0.15915493667125701904 は 1/(2π) の 単精度丸め です。引数ラジアンを 0〜2π → 0.0〜1.0 に正規化するレンジリダクションの一部と考えられます（詳細は後述）。
コードと .ncu-rep は以下に置いてあります：

https://github.com/toropippi/cuda_sinf_profile_benchmark

 命令-SASS対応表すべての sin/cos が同じく近似経路になるわけではありません。Intrinsic（__sinf/__cosf など）はハードウェア経路、標準関数（sinf/cosf）はデフォルトで libdevice によるソフトウェア実装（高精度）です。ソフトウェア実装は精度が高いかわりにFMA系命令で近似式をエミュレーションするので計算時間は長めです。ビルドオプションで切り替え可能な命令もあります。


書き方（デバイス関数）
型
コンパイルoption
代表的SASSシーケンス（概念）
実装の種別
精度/備考


__sinf(x)
float
なし
（sm_50〜sm_70）RRO.SINCOS → MUFU.SIN /（sm_75+）FMUL x, x, 1/(2π) → MUFU.SIN

ハードウェア（MUFU/SFU）
近似・高速。MUFUに直結する薄いラッパ。(NVIDIA Docs, NVIDIA Developer Forums)

sinf(x)
float
なし
多数のFMA等（長いポリノミアル＋レンジリダクション）
ソフトウェア（libdevice）
高精度・遅め。SFUは使われない。(NVIDIA Developer Forums)

sinf(x)
float

-use_fast_math（nvcc）
__sinf(x)と同様（MUFU経路）
ハードウェア（MUFU/SFU）
近似・高速。sinfが実質__sinf相当へ。(NVIDIA Developer Forums, tschmidt23.github.io, releases.llvm.org)

__sincosf(x, &s, &c)
float
なし

RRO.SINCOS（または FMUL 正規化）→ MUFU.SIN と MUFU.COS

ハードウェア（MUFU/SFU）
sinとcosを同時に出す最速手。範囲縮小を1回で共有。(NVIDIA Developer Forums)

sincosf(x, &s, &c)
float
なし
多数のFMA等
ソフトウェア（libdevice）
高精度・やや遅い。(NVIDIA Developer Forums)

sin(x)
double
なし
多数のFMA等（長いソフト実装）
ソフトウェア（libdevice）
ハードウェア命令は存在しない（DPのMUFUはない）。(NVIDIA Developer Forums, NVIDIA Docs, カーネギーメロン大学コンピュータサイエンス学校)


 補足1 SASSの違い古い世代（〜sm_70）ではRRO.SINCOS命令（範囲縮小）→MUFU.SIN/COSの並びが一般的。

Turing以降（sm_75+）では、MUFUのインターフェイス変更により、FMUL x, 1/(2π) → MUFU.SIN のような短い並びになることがある（RRO不使用）(NVIDIA Developer Forums)。

 補足2 double倍精度sin(double)は常にソフトウェア(NVIDIA Developer Forums)。

 補足3 libdevice標準の sinf/cosf/sin などは、デフォルトで libdevice（ポリノミアル＋厳密なレンジリダクション等）に展開されます。詳細は libdevice ユーザーズガイドを参照(NVIDIA Docs

)

 主要なGPUには超越関数ユニットがあるようだが・・話を少し戻します。

NVIDIAのFermi以降GPUアーキテクチャには特殊関数ユニット (SFU) と呼ばれるハードウェアが搭載されており、sin,cos,exp,log,rcp,rsqrt を高速に近似計算することができます。用語として「SFU」はほぼNVIDIA用語ですが、AMD/Intel/Adreno などにも同種のハード機能が存在します。

で、ここからが重要というかややこしい話なのですが、どのGPGPU API／書き方でSFUに乗るのか、近似の精度・速度はどれくらいか、ベンダー差は…と様々な疑問がわき上がり膨大な検証が必要です。その検証記事の前提知識となるようにこの記事を書いておく必要があったのです。

 0.15915493667125701904 の考察
 3.1415...に最も近い32bit floatのbit表現は？-----一部抜粋-----
     FMUL.RZ R9, R5, 0.15915493667125701904
     MUFU.SIN R5, R9
-----------------
SASSにでてきた 0.15915493667125701904 ですがもう少し考察してみました。これは1/(2π) のことでした。これが最適な値でしょうか？

0.15915493667125701904 を float32 にすると、ビット表現は
0x3e22f983
であり有効桁数40桁で再度10進数にもどすと
0.1591549366712570190429687500000000000000
です。

逆数をとって2で割るとπに近い値になりますが
3.1415927803281187284699411752424
^^^^^^^265358979323846264338....(正解の値)
と3.141592のところまでしか正確でないことがわかります。
実際のπより少しだけ大きい値を使っていることがわかりました。では1bitだけずらして次に小さい値はいくつでしょうか？
0x3e22f984
の10進数表現を逆数にして2で割ると
3.1415924861909903350976358496085
^^^^^^^265358979323846264338....(正解の値)
ということで0x3e22f983のほうが 1/(2π) に近い値であることがわかりました。

 なぜRZ（0方向丸め）なのかFMUL.RZとあるように普通の近接丸め(RN)ではないRZを使っています。正直なぜなのかはわかりません。

先程の 0.15915493667125701904 は実際の1/2πより少し小さい値であることがわかっています。ということはFMULした後の値も実際より少し小さい値であるはずなので最近接偶数丸めや無限方向に丸めたほうが近くなるはずです。

このあとMUFU.SINに値を流すうえで必要なことなのかもしれませんが、ベンダーの思想が絡んでそうでこれ以上の考察は難しそうです。

 2πで割るのは四分円マッピング,小区間分離をしやすくするため(予想)鍵となる考え方は 四分円分割 です。
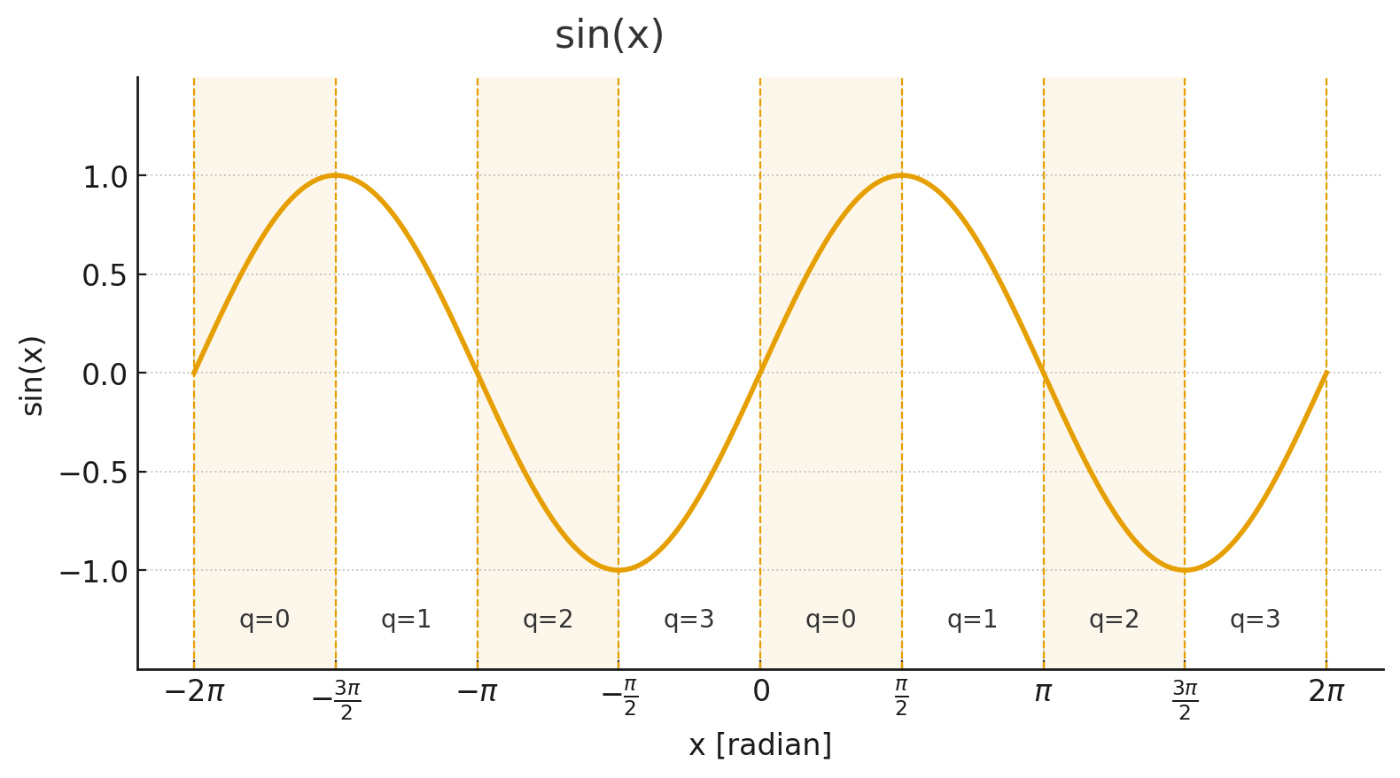
sin関数のグラフを見るとxが π/2 ごとに曲線が同じパターンとなっていることがわかります。この パターン を小区間専用のルックアップテーブルなどで求めるとして、あとは上下反転や左右反転だけでsin cos関数を再現することができそうです。
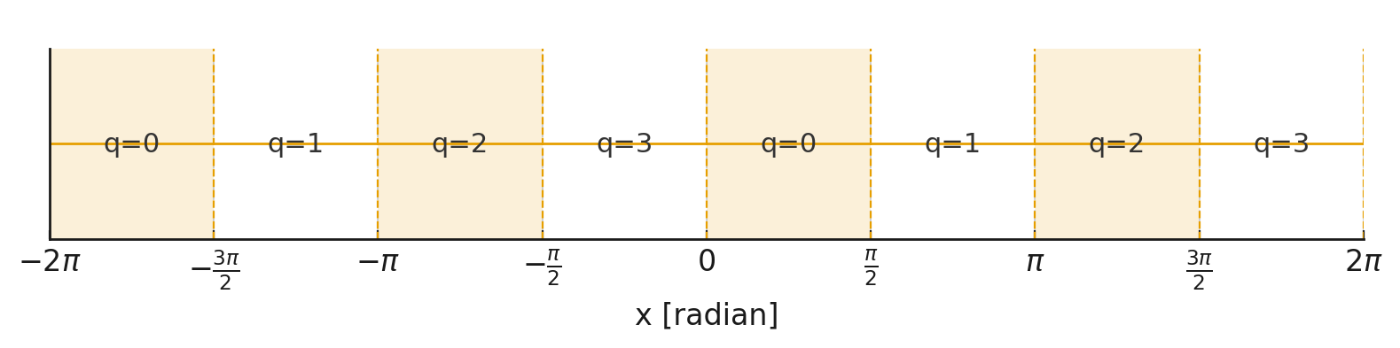
四分円インデックスをqとして、あまりの部分をyとすれば


q
sin(x)
cos(x)


0
+ S(y)
+ S(π/2 - y)

1
+ S(π/2 - y)
− S(y)

2
− S(y)
− S(π/2 - y)

3
− S(π/2 - y)
+ S(y)

※ここで S(u) ≈ sin(u) は小区間専用の近似（多項式やテーブル補間）
こんなかんじに答えをだすことができます。qとyを求めるところはラジアン角のままではやりにくいですが 2π で割っておくことで簡単に求まります。具体的には4.0でかけて整数分離するとqが、小数分離するとyが求まります。4.0でかける操作は仮数部に影響を与えないので精度劣化は発生しません。

これが0.15915493667125701904をかけておく理由なのではないでしょうか。

（じゃあなぜ π/2 で割らないのかはわかりません）
Sまわりの計算ですが、これは上図の上下反転や左右反転の話で、入力側の位相シフトと（π/2-yは加減算のみで済む）出力側の+-反転で再現でき回路的に難しくないはずです。

以下にFMULからMUFU.SINの流れについてフローチャートの"イメージ"をつくりました。あくまで私のイメージですよ

 その他疑問等
 ・SFUの内部実装はどうなってる？公開されてないので不明です

が、内部でテーブル参照＋多項式補間 の可能性が高いんじゃないかと私のChat GPTが言ってました（考察の図はあくまで概念説明です）

 ・MUFU.SINの実行スループットは？1サイクル/1SFUです (【Zenn】GPU命令レベルで読む...)

通常FP32コアとSFUの比が4:1～8:1なので当然スループット比も4～8分の1となります

 ・MUFU.SINはFMA系命令と計算をオーバーラップできる？できます (【Zenn】GPU命令レベルで読む...)

 最後にこの記事をかくにあたり既報の調査、表の生成、記事の校正にChat GPT 5 (2025/8/28)を使用しました。

検証結果についてはすべて著者が確認しております。

q	sin(x)	cos(x)
0	`+ S(y)`	`+ S(π/2 - y)`
1	`+ S(π/2 - y)`	`− S(y)`
2	`− S(y)`	`− S(π/2 - y)`
3	`− S(π/2 - y)`	`+ S(y)`

書き方（デバイス関数）	型	コンパイルoption	代表的SASSシーケンス（概念）	実装の種別	精度/備考
`__sinf(x)`	`float`	なし	（sm_50〜sm_70）`RRO.SINCOS` → `MUFU.SIN` /（sm_75+）`FMUL x, x, 1/(2π)` → `MUFU.SIN`	ハードウェア（MUFU/SFU）	近似・高速。MUFUに直結する薄いラッパ。(NVIDIA Docs, NVIDIA Developer Forums)
`sinf(x)`	`float`	なし	多数のFMA等（長いポリノミアル＋レンジリダクション）	ソフトウェア（libdevice）	高精度・遅め。SFUは使われない。(NVIDIA Developer Forums)
`sinf(x)`	`float`	`-use_fast_math`（nvcc）	__sinf(x)と同様（MUFU経路）	ハードウェア（MUFU/SFU）	近似・高速。`sinf`が実質`__sinf`相当へ。(NVIDIA Developer Forums, tschmidt23.github.io, releases.llvm.org)
`__sincosf(x, &s, &c)`	`float`	なし	`RRO.SINCOS`（または `FMUL` 正規化）→ `MUFU.SIN` と `MUFU.COS`	ハードウェア（MUFU/SFU）	sinとcosを同時に出す最速手。範囲縮小を1回で共有。(NVIDIA Developer Forums)
`sincosf(x, &s, &c)`	`float`	なし	多数のFMA等	ソフトウェア（libdevice）	高精度・やや遅い。(NVIDIA Developer Forums)
`sin(x)`	`double`	なし	多数のFMA等（長いソフト実装）	ソフトウェア（libdevice）	ハードウェア命令は存在しない（DPのMUFUはない）。(NVIDIA Developer Forums, NVIDIA Docs, カーネギーメロン大学コンピュータサイエンス学校)

SASSをみてみる

命令-SASS対応表

補足1 SASSの違い

補足2 double

補足3 libdevice

主要なGPUには超越関数ユニットがあるようだが・・

0.15915493667125701904 の考察

3.1415...に最も近い32bit floatのbit表現は？

なぜRZ（0方向丸め）なのか

2πで割るのは四分円マッピング,小区間分離をしやすくするため(予想)

その他疑問等

・SFUの内部実装はどうなってる？

・MUFU.SINの実行スループットは？

・MUFU.SINはFMA系命令と計算をオーバーラップできる？

最後に

Discussion