木DPから学ぶ、動的計画法の構造と双対性
はじめに
こんにちは、とりからです。
今回は動的計画法について、ボトムアップとトップダウンの二種類の木DPをきっかけに、「貰う」DPと「配る」DPの構造とその双対性を明確にしていくことで、アルゴリズムの理解を深めていきたいと考えています。
DP自体の初歩は前提とし、「DPテーブルの更新をどうするかで迷う人」「DPは漸化式だと言われてもピンとこない人」「基本的なナップサックは書けるけど、応用的な問題では状態をどう持てばいいかわからない人」などを対象に、理解の手助けとなれば幸いです。
動的計画法(DP)とは
DPとは、そのまま解くには計算量が大きすぎる問題について、小さな部分問題に分解し、それらの解を統合することによって、全体の問題の解を得るアルゴリズムです。
このアルゴリズムを有効に機能させるためには以下の条件を満たす部分問題への分解が重要です。
- 部分問題が十分に小さい計算量で解決可能であること
- 部分問題の統合として、全体の解が表現可能であること
- 部分問題の統合にかかる計算量が十分に小さいこと
DPの難しさは、適切な部分問題への分割(=状態の選択)と、統合の方法の選択(=遷移構造の決定)にあります。
以降で、DPの構造を明確化していく中で、このあたりがクリアになればと思います。
「配る」と「貰う」とは
DPを特徴付ける要素として、「配る」か「貰う」かというものがあります。まず、これらの特徴の相違点について説明していきます。
「配る」DPとは
- 遷移の軸は、「解決した部分問題」にある
- 部分問題の解が、次のどの問題に寄与するのかという形で、解の伝播を行う
- すなわち、1対多の構造で解を伝播していく
この特徴から、自明な初期状態における部分問題を解決し、そこからトップダウンで全体問題を解決していくようなDPを自然に構築できます。
「貰う」DPとは
- 遷移の軸は、「未解決の問題」にある
- 未解決の問題の解は、どの解決済の部分問題を集約することで得られるかという形で、解の集約を行う
- すなわち、他対1の構造で解を伝播していく
この特徴から、自明な複数の最終状態における部分問題を解決して、そこからボトムアップで全体問題を解決していくようなDPを自然に構築できます。
木DPから見える双対性
上記の「配る」か「貰う」かという構造がわかりやすい例として木DPを挙げます。
例えば、各ノードの根からの深さを求めようとしたとき、根自身の深さは自明に0となります。これを起点に各子ノードに伝播(配る)し、子ノードの深さは「親ノード+1」としていけば、葉に至るまで各ノードの深さを求めることができます
また、あるノードを根としたときに、各ノードが持つ部分木のサイズを求めようとしたとき、葉の持つ部分木のサイズは自明に1(自身のみ)となります。これを起点に各親ノードが集約(貰う)し、親ノードの持つ部分木サイズは「子ノード達のもつ部分木サイズの和に1を足す」とすれば根に至るまで各ノードの持つ部分木サイズを求めることができます。
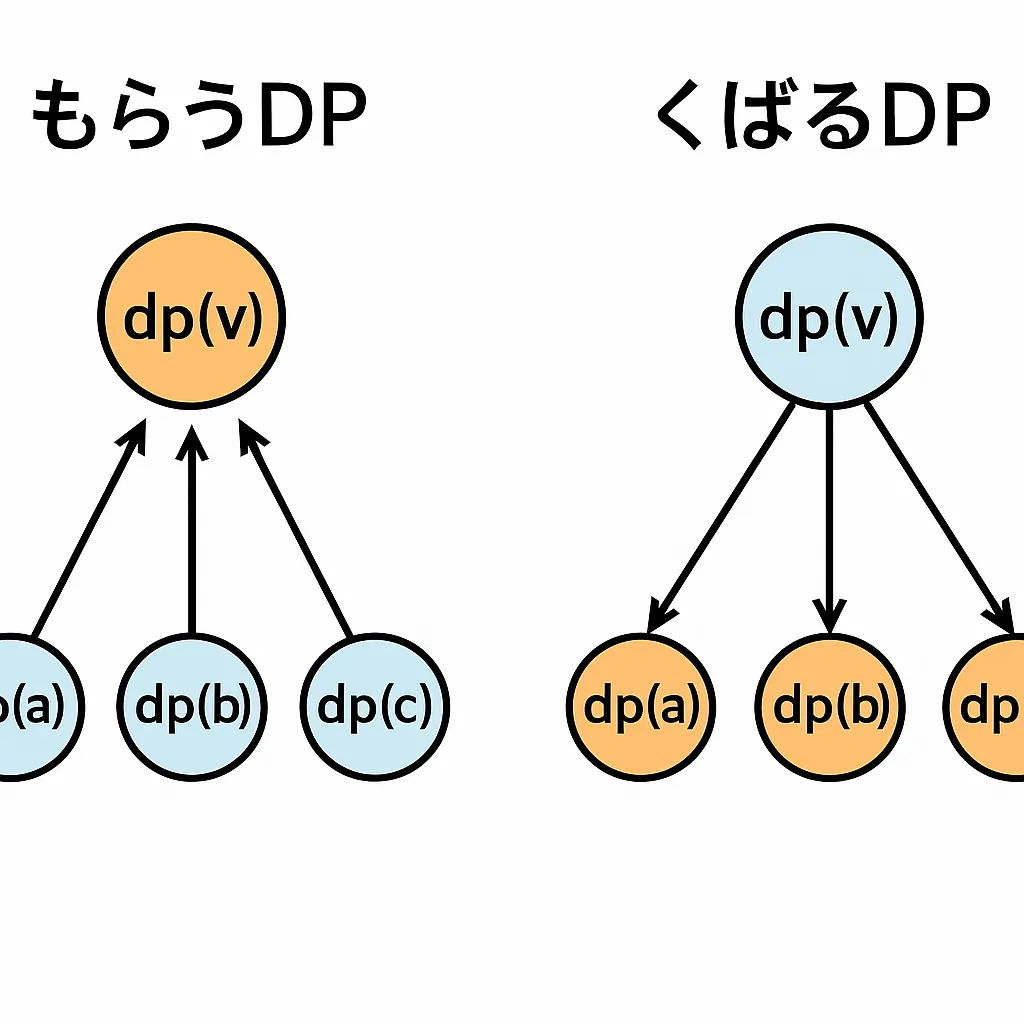
このように、木DPにおいては「配る」と「貰う」の関係性が明確であり、根から葉に向けて伝播、子から親に向けて集約という、双対的な構造をもつことがわかります。(イメージ図はAIに作成してもらいました)
対称性の破れ
ここまで「配る」と「貰う」の間に双対的な構造が存在することを見てきました。
とすれば、これらの二つはどちらを選択してもよく、極論すれば、どちらか一方で書けば十分ではないか、と思うかもしれません。
実際、どちらでも書けるDPも少なくありません。
しかし、DPの双対性の中で、1対多と多対1という遷移に由来する非対称性が、現実的にはどちらかでしか書けない、あるいは一方で書く方が自然、効率的に書けるといった状況を生むことがあります。
個人的には、解決した問題にスポットをあてて、次どこへ遷移するかを考えられる「配る」が好きなのですが、それだけではダメだったということです。
ここからはそういった非対称性について見ていきます。
遷移構造による非対称性
DPの遷移は、繰り返しになりますが1対多、多対1という構造を持ちます。この構造を処理しやすい向きが自然な向きとして定まることがあります。
- bitDPの場合
状態
- 全方位木DP(rerooting)
根を取り直す際に、これまでの根から子へ情報を渡すことになりますが、この時一部の子(新たに根となる子)の情報を除いたものを渡す必要があります。この部分で貰う構造であれば明示的に一部の子を除いて集約する自然な形が浮かびますが、配る構造では、除く部分の管理が煩雑になりそうです。
一般にDPの遷移は、始点から情報の伝播を有向グラフで表現してみると、DAGとなることがわかります。このDAGを眺めてみて、入次数と出次数の数や、遷移の依存関係等を確認することで自然な遷移構造が見えてくるかもしれません。
データ構造による非対称性
1対多や多対1の遷移における「多」が大きすぎて、要求される計算量で単純に実行できない場合高速化を検討する必要があります。この高速化において、「配る」側ができることと「貰う」側ができることに非対称性があります。
具体的にはデータ構造等を用いた情報の集約により「貰う」DPを簡単に高速化することができる場合があります。
連続する区間の和を貰うようなケースでは、累積和を用いることで、効率的に値を「貰う」ことができるでしょうし、あまりに貰うものが多い場合には、余事象を考慮して必要な値だけを「貰う」ことで効率化することも考えられます。またセグメントツリーを用いることで、情報の集約を高速に行うことも考えられます。
まとめ
- 配るDPとは1対多の遷移、貰うDPとは多対1の遷移
- 配るDPと貰うDPは理論的には双対的な関係性を持つ
- 実装上は必ずしも対称性が保持できるわけではなく、いずれかのDPの方が自然に、効率的に書けるケースが存在する
- 上記のような遷移設計をどう行うかがDPの肝であり、遷移の起点をどのようにとるか、遷移のDAG構造がどうなるかといった点をふまえて設計する必要がある
- 特に計算量の制約から高速化が必要な場合は、貰うDPにしてデータ構造の活用を検討することも必要
おわりに
今回はDPについて、木DPをきっかけにその構造と性質を整理してきました。ここまで読んでくださった方に何か得るものがあれば幸いです。今後もまたアルゴリズム等の記事を投稿しますので、その際も読んでいただけると嬉しいです。みなさまが良きDPライフを送れますように
Discussion