Zenn
📸

乱数と1ピクセルで写真を撮る方法（ゴーストイメージングへの招待）

2023/02/19に公開
画像処理
光学
イメージング
ゴーストイメージング
tech

はじめに

カメラといえば一度シャッターを切れば日常の一部を画像として保存することができます。これは撮像（イメージング）と呼びます。一般的にカメラは光を受ける箇所が二次元的に配置されているため、画像情報としてメモリに納めることができるわけですが、この受光箇所が一つしかなかったらどうでしょうか？二次元的な空間の広がりを持たないので画像として参照するのは困難なように見えます。しかしそれを実現するのがゴーストイメージングという技術です。
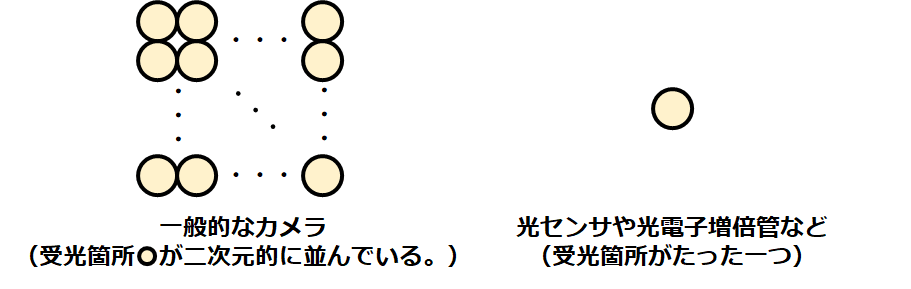
カメラと1ピクセル受光器

ゴーストイメージング

先ほど紹介した各受光箇所はピクセルといい、これは画像のピクセルにそのまま対応します。ゴーストイメージング（Ghost Imaging）は乱数を通じて生成された0と1の"パターン"を次々に撮像対象に照射、その光を1ピクセルの受光素子でキャッチします。キャッチした情報をもとにPC上で撮像対象を再構成していきます。

ゴーストイメージングの概要図

シミュレーション結果ではありますが、GIという文字がイメージングできていく様子を見てみましょう。

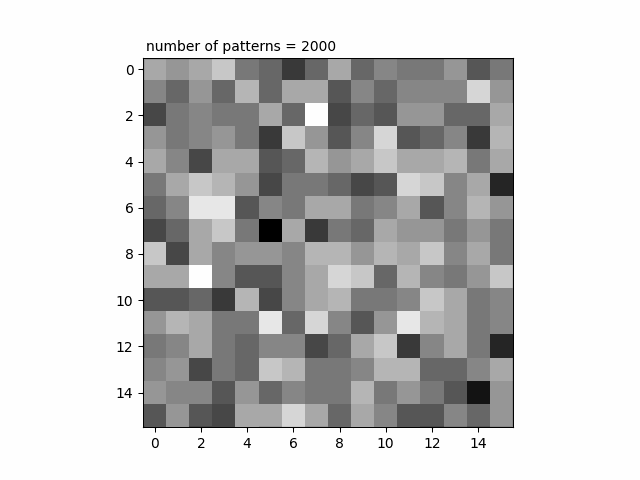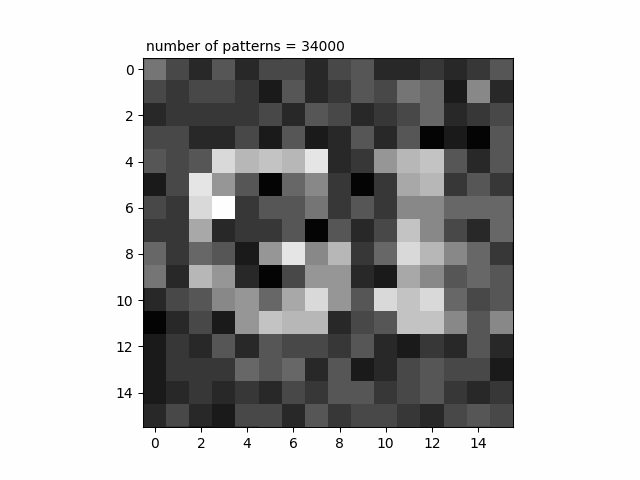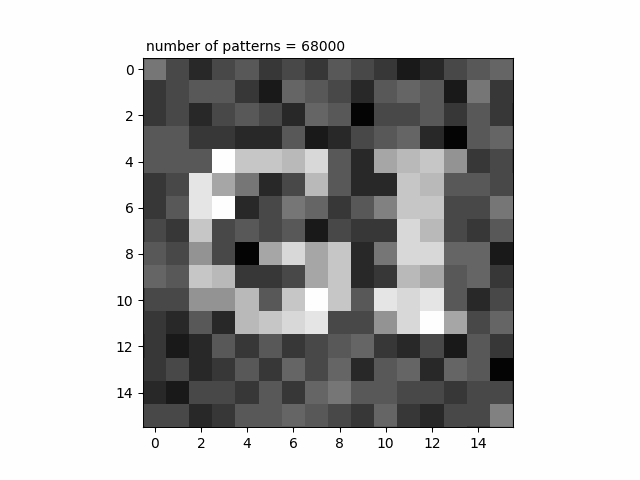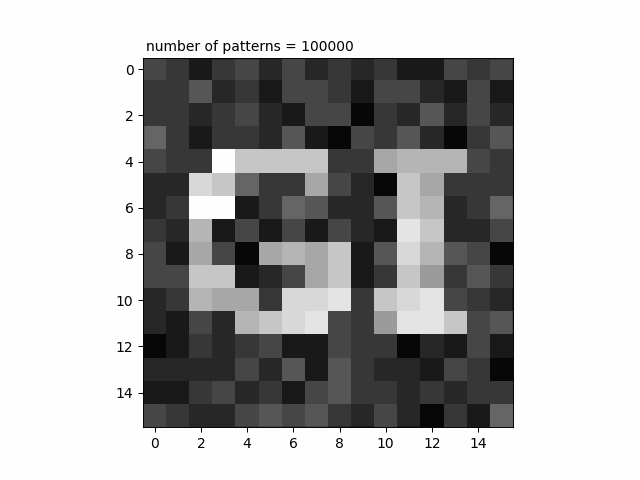
シミュレーション結果

number of patternsは照射したパターンの枚数を表しています。パターンの枚数を増やしていけばいくほどGIという文字が浮かび上がっていくのが分かります。

ゴーストイメージングの原理

実はパターンを照射して受光素子で光をキャッチする一連の流れは統計学で使われる相関を計算していることと同じです。受光素子に入射する光からはそのエネルギーとして光強度と呼ばれる量が取得できます。この光強度がパターンと撮像対象の相関を表しており、この相関が大きければ大きいほど撮像対象はそのパターンをより多く含んでいると捉えることができます。[1]

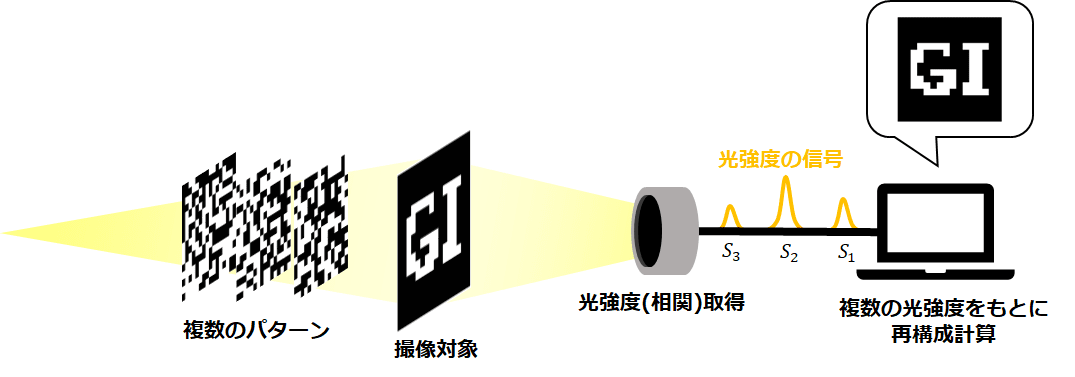
ゴーストイメージング原理図

照射したパターンは予め分かっているものと仮定し、次の図のような計算をPC内で実行すればGIという文字が浮かび上がってきそうです。

再構成計算

つまりパターン自体に光強度(相関)をかけ合わせることで、より撮像対象に似ているパターンを優先的に主張させられるので撮像対象が再構成できるということです。本記事ではこの計算を再構成計算と呼ぶことにします。

相関とは？

上で説明した原理の部分を数式で確認してみましょう。相関とは異なる二つのデータがどれだけ似ているかを表す指標で、似ていれば似ているほど大きな値を取るものです。数式で表すとこんな感じです。

r = \frac{\sum_{n=1}^{N}a_{n}b_{n}}{\sqrt{\sum_{n=1}^{N}(a_{n})^{2}}\sqrt{\sum_{n=1}^{N}(b_{n})^{2}}}

これは相関の中でも相関係数と呼ばれるもので-1から1の範囲を取るものです[2]。ここで新たにデータ列を

\mathbf{a}=(a_{1},a_{2},\cdots,a_{N}),\;\mathbf{b}=(b_{1},b_{2},\cdots,b_{N})

と置いて、

\langle\mathbf{a},\mathbf{b}\rangle=\sum_{n=1}^{N}a_{n}b_{n}

を定義しましょう。これはベクトル\mathbf{a},\mathbf{b}の内積と呼ばれます。結論、相関を計算するということは内積を計算するということになります。なので乱暴ですが相関＝内積とみなせます。これは相関係数の分子の話でしたが、分母は正規化のための計算なので無視で問題ないです。

一旦離散的なデータを扱ってきましたが空間という連続なものを考えるならば、二次元の場合ベクトルではなくf(x,y)という二変数関数で表されます。ここで関数f(x,y),g(x,y)の内積はベクトルの時a_{i},b_{i}と同じインデックス同士の積の総和だったのに対して関数では

\langle f,g\rangle=\iint_{\mathcal{A}}f(x,y)g(x,y)dxdy

同じ二次元座標同士の積の積分で定義されます。

ゴーストイメージングによる相関計算

受光素子に光が入射するとその光のエネルギーとして光強度が取得できます。とある二次元上の点(x,y)における光u(x,y)の光強度I(x,y)は次式で定義されます。

I(x,y)=|u(x,y)|^{2}

この光を受光素子でキャッチすることを考えます。
受光素子で光をキャッチ

このとき光を受け取る領域（開口）を\mathcal{A}とおけば、受光素子から得られる全光強度Sは

S = \iint_{\mathcal{A}}|u(x,y)|^{2}dxdy

で計算されます。次に撮像対象にパターンを通過させる部分に注目します。

撮像対象にパターンを作用

ここで撮像対象をt(x,y)、n番目に照射するパターンをp_{n}(x,y)で定義すると撮像対象を通過した直後の光u(x,y)は

u(x,y)=t(x,y)p_{n}(x,y)

と単純に掛け算した結果になります[3]。これは撮像対象にパターンを作用させると言います。そのままこの光が受光素子に入射したならば受光素子上で得られる全光強度S_{n}は、

\begin{align*} S_{n} &= \iint_{\mathcal{A}}|u(x,y)|^{2}dxdy \\ &= \iint_{\mathcal{A}}|t(x,y)p_{n}(x,y)|^{2}dxdy \\ &=\iint_{\mathcal{A}}|t(x,y)|^{2}p_{n}(x,y)dxdy = \langle T,p_{n}\rangle \end{align*}

となります[4]。ここでパターンが0か1の値をもつことからp_{n}(x,y)=|p_{n}(x,y)|^{2}を利用しました。またT=|t(x,y)|^{2}で定義しました。このTは撮像対象の光強度を反映しており、受光素子で得た全光強度はパターンと撮像対象の強度情報の相関になることが確認できました。

再構成計算

そのまま一番最初に紹介した再構成計算を数式で記述します。再構成結果を\tilde{T}とするならば、

\tilde{T}(x,y)=\sum_{n=1}^{N}S_{n}p_{n}(x,y)

で書けます。ここでNは照射したパターンの枚数です。Nをより大きくしていくとだんだんとTに近づいていきます。すなわち再構成されるものは撮像対象の強度情報ということになります。

ここで再構成されるのはt自身でなくて問題ないのか？という疑問があるかもしれません。そもそもゴーストイメージングに限らず一般的なイメージングは受光素子から光をキャッチすることを考えると結局得られるものはその強度情報になります。我々は強度情報を通じて物体の認識を行っていると言えます[5]。

とはいえ再構成結果が正しいかどうか判別するにはtにどれだけ近いか調べる必要があります。はじめに紹介したGIという文字の再構成結果は、撮像対象も0か1の二値を取るように設定しているためt=Tが成り立ちます。0は光を通さない、1は光を通すという物理的な意味を持ち、これで再構成結果自体はtに近づいていきます。そしてこの時の再構成結果\tilde{t}を

\tilde{t}(x,y)=\sum_{n=1}^{N}S_{n}p_{n}(x,y)

と置きましょう。ここでS_{n}=\langle t,p_{n}\rangleであることも付け加えておきます。さらに再構成結果の評価としてMSE（平均二乗誤差）を使います。MSEは次の定義です。

MSE=\frac{1}{N_{h}N_{w}}\sum_{i=1}^{N_{h}}\sum_{j=1}^{N_{w}} (t_{i,j}-\tilde{t}_{i,j})^{2}

ここでt_{i,j}は撮像対象のi,jに位置するピクセルの値です。\tilde{t}_{i,j}は再構成結果のi,jに位置するピクセルの値です。N_{h},N_{w}は高さと幅のピクセル数です。MSEは0に近ければ近いほど高い精度で再構成できていることを表します。実際にパターンを最大10万枚使った時のMSEの推移を見てみましょう。

MSE
縦軸：MSE、横軸：照射したパターン枚数N

パターンを照射すれば照射するほど精度高く再構成できるようになることが確認できました！[6]

もっと良い再構成方法

これまでゴーストイメージングにおける一連の流れを説明しました。しかし再構成をするのに10万枚もパターンを使ってられません。一般的なゴーストイメージングにおいて実は先ほど紹介した再構成計算を使われるのは稀です。結論から言うとよく使われるのは次の方法です。

\tilde{t}(x,y)=\sum_{n=1}^{N}(S_{n}-\langle S_{n}\rangle)p_{n}(x,y)

ここで\langle S_{n}\rangleは

\langle S_{n}\rangle = \frac{1}{N}\sum_{n=1}^{N}S_{n}

であり、S_{n}のアンサンブル平均と呼びます。以後\langle \cdot\rangleの形で書かれたものはそのアンサンブル平均とします。このときパターンを照射していった時の再構成結果を見てましょう。

シミュレーション結果（平均値あり）

はじめに紹介したものと同じ10万枚照射していますが明瞭な像が得られていますね。ついでにMSEも見ておきましょう。

MSE比較
青：アンサンブル平均なし（上）、オレンジ：アンサンブル平均あり（下）

明らかに少ないパターン枚数で高い精度を叩き出しているのが分かります。そもそもこの再構成計算は何をしているのでしょうか？まずS_{n},p_{n}(x,y)を新たに次で表現しましょう。

S_{n} =\langle S_{n}\rangle + \Delta S_{n},\; p_{n}(x,y) = \langle p_{n}(x,y)\rangle + \Delta p_n(x,y)

\Delta S_{n}と\Delta p(x,y)はS_{n}とp(x,y)の偏差です。\tilde{t}(x,y)をパターン枚数Nで割って式整理しましょう。

\begin{align*} \frac{\tilde{t}(x,y)}{N} &= \frac{1}{N}\sum_{n=1}^{N}(S_{n}-\langle S_{n}\rangle)p_{n}(x,y) \\ &= \frac{1}{N}\sum_{n=1}^{N}(\langle S_{n}\rangle + \Delta S_{n}-\langle S_{n}\rangle)(\langle p_{n}(x,y)\rangle + \Delta p_n(x,y)) \\ &= \frac{1}{N}\sum_{n=1}^{N}\Delta S_{n}\langle p_{n}(x,y)\rangle+\frac{1}{N}\sum_{n=1}^{N}\Delta S_{n}\Delta p_{n}(x,y) \\ &=\langle \Delta S_{n}\rangle\langle p_{n}(x,y)\rangle+\langle \Delta S_{n}\Delta p_{n}(x,y)\rangle \end{align*}

ここでS_{n} =\langle S_{n}\rangle + \Delta S_{n}より\langle \Delta S_{n}\rangle=0なので最終的に、

\frac{\tilde{t}(x,y)}{N} = \langle \Delta S_{n}\Delta p_{n}(x,y)\rangle

で整理できます。つまり平均からの強度とパターンの値の偏差\Delta S_{n},\Delta p_{n}(x,y)を使って再構成しているということが明確になりました。再構成結果をこのように記述されることもあります。

なぜ1ピクセルで受光する必要があるのか？

これまでイメージングできなかったものがイメージングできるようになるかもしれないからです。

一般的にカメラとして挙げられる受光素子はCCDカメラやCMOSカメラと呼ばれるものです。これらが受光部分が二次元的に配列しているわけですが、受光部分がたった一つであってもイメージングできるようになれば、様々な受光素子を使うことができるようになり、これまでのカメラが取得できなかった波長帯や分解能でイメージングできるようになるはずです。

また乱数を使うとノイズ耐性のあるイメージングができるようになるとのことです。ノイズというと機器的なノイズや空間上のノイズなど様々挙げられますが、ノイズ自体が重ね合わせていくと軽減することと乱数がノイズを受けても乱数としての性質を保つことを考えれば、確かにノイズ耐性のあるイメージングができるようになりそうです。

ただゴーストイメージングには欠点があります。うすうす気づいているかと思いますがパターンを何度も照射しなければならないということです。

ゴーストイメージングに限らず1ピクセルでイメージングする技術は、必ず複数回のパターンの照射が必要になります。このパターンの照射をできるだけ減らすために圧縮センシングや深層学習などを組み合わせて、できるだけパターン照射の回数を減らす努力がなされています。

シミュレーション用ソースコード

パッと見何をしているかわかりづらくてスイマセン（´・ω・｀）今回の記事の結果は以下のコードで実施しました。実行する際は自己責任でお願いします。main関数内のパラメータを変化させれば様々実験できます。本ソースコードは次の環境で実施しました。

  • OS: Windows 11
  • Python: 3.9.13
  • matplotlib: 3.6.3
  • numpy: 1.24.1
  • Pillow: 9.4.0

https://github.com/torataro-tiger/GIsimulation/blob/ff0a895dd4c3521f1f7e599e345fc1e40fd971ba/ghostImaging.py

参考文献

公益社団法人 精密工学会 Precipedia「ゴーストイメージング」http://precipedia.jspe.or.jp/wiki/index.php?title=ゴーストイメージング

脚注

  1. 後で示しますが正確には撮像対象の強度情報との相関です。 ↩︎

  2. 前提としてデータ\{a_{i}\}_{i\in\mathbb{N}}と\{b_{i}\}_{i\in\mathbb{N}}は平均値が0であることを要求します。 ↩︎

  3. この掛け算が成り立つためには撮像対象が十分薄いことを仮定します。厚い物体の場合は原子核物理学などで使われる散乱問題として定式化する必要があります。ボルン近似ってやつですね。 ↩︎

  4. 本当はいろいろ突っ込みどころがあります。本来光は波なので空間中を回折しながら進みます。つまりパターンはパターンのまま撮像対象に伝搬するわけはでないし、撮像対象を通過した後も通過した直後の光がそのまま受光素子に届くわけではありません。ただレンズなどの光学素子を使えばうまくパターンのまま伝搬させることができます（4f光学系など）。撮像対象を通過した後も同様です。ここは簡単のためにそのような仮定があることに注意してください。 ↩︎

  5. 実はt自身を取得する技術もあります。それがホログラフィです。受光素子から光強度が得られると説明しましたが、この光強度に波の干渉を反映することでうまい具合にt自身を観測できるようになります。このとき画像ではなく立体的に情報を認識できるようになります。 ↩︎

  6. 撮像対象と直接比較できるように\tilde{t}を0から1に正規化して評価しています。 ↩︎

Discussion