10分で論文略読: The Byzantine Generals Problem (1982)

The Byzantine Generals Problem

1. LAMPORT, Leslie; SHOSTAK, Robert; PEASE, Marshall. The Byzantine Generals Problem. In: ACM Transactions on Programming Languages and Systems, Vol.4, No.3. 1982.

1. Introduction

システムを構成するコンポーネントの故障は敵陣を包囲するビザンツ軍に例えることができる。この要件は:

• A. 忠実な将軍たちはすべて同じ作戦行動をとる。
• B. 少数の裏切り者たちは忠実な将軍たちに不正な作戦を採用させることができない。

A が成立するためには:

1. 任意の 2 人の忠実な将軍は同じ値 $v(i)$ を使用する。
2. もし将軍 $i$ が忠実であれば、彼が送った値はすべての忠実な将軍によって $v(i)$ として使用されなければならない。

対話的整合性: $n$ 人の将軍のうち、1人の司令官と他の $n-1$ 人の副官は:

• IC1. すべての忠実な副官は同じ命令に従う。
• IC2. 司令官である将軍が忠実であれば、すべての忠実な副官は彼の送る命令に従う。

司令官が忠実であれば IC2 から IC1 を導くことができる。論文中の説明の多くは自明な IC2 から開始して司令官が裏切り者である場合の IC1 を証明する方法で説明している。

2. Impossibility Results

メッセージに署名を付けない構成では $m$ 人の裏切り者に対して $3m+1$ より少ない将軍でのビザンチン将軍問題の解は存在しない。

例えば下限の $m=1$ では 3 将軍での解は存在しない。副官 1 が矛盾した値を得たとき、司令官と副官 2 のどちらが裏切り者かを判断できないため IC1, IC2 を満たすことができない。

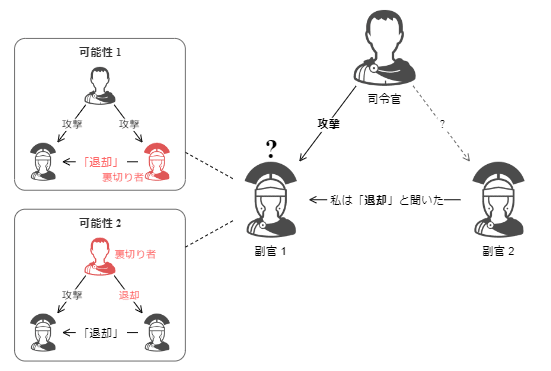
メッセージに署名を付けない構成では、裏切り者が $m$ 人いるケースでビザンチン将軍問題を解くには少なくとも $3m+1$ が必要。

A Solution with Oral Messages

署名を付けないメッセージ (口伝メッセージ) での要件:

• A1. 送信されたメッセージは正しく配信される。
• A2. メッセージの受信者は誰がメッセージを送信したかを知っている。
• A3. メッセージの欠落を検出することができる。

${\rm majority}(v_1,\ldots,v_{n-1})$ は $\{v_1,\ldots,v_{n-1}\}$ の過半数が $v$ と等しいとき値 $v$ を返す関数とする。または $\{v_1,\ldots,v_{n-1}\}$ が順序集合の場合はその中央値を返す関数でも良い。

アルゴリズム ${\rm OM}(m)$

$m$ 人の裏切り者が存在する場合に $3m+1$ 人以上の将軍がいればビザンチン将軍問題を解決できる。

${\rm OM}(0)$ のケース

1. 司令官は副官に命令を送信する。
2. 副官は司令官から受信した値を使用する。受信しなかった場合は RETREAT (退却) とする。

${\rm OM}(m), m \gt 0$ のケース

1. 司令官は副官に命令を送信する。
2. 各副官 $i$ が司令官から受信した値を $v_i$ とし、受信しなかったら RETREAT とする。副官 $i$ は ${\rm OM}(m-1)$ の司令官として動作し、値 $v_i$ を他の $n-2$ 人の副官すべてに送信する。
3. $i \ne j$ となる各副官 $i$ が副官 $j$ から受信した値を $v_i$ とし、受け取らなければ RETREAT とする。副官 $i$ は ${\rm majority}(v_1,\ldots,v_{n-1})$ を使用する。

定理 1. 任意の $m$ に対して、$3m$ より多い将軍と $m$ 人の裏切り者が存在する場合、アルゴリズム ${\rm OM}(m)$ は IC1 と IC2 を満足する。

A Solution with Signed Messages

署名付きメッセージ構成での追加の要件。

• A4. (a) 忠実な将軍の署名は偽造できず、署名さえたメッセージはいかなる変更も検出できる。(b) 誰でも将軍の署名の真偽を検証できる。

アルゴリズム ${\rm SM}(m)$

$i$ によって署名された値 $v$ を $v:i$ と表記する。つまり $v:i:j$ は $i$ によって署名された値 $v$ をさらに $j$ が署名したものを表す。司令官を $0$ とする。将軍 $i$ の受信している値の集合を $V_i$ とし、初期値 $V_i=\emptyset$ とする。

1. 司令官は自信の値に署名してすべての副官に送る。
2. 副官 $i$ それぞれに対して:
   1. $i$ が司令官から $v:0$ を受信し、$v$ が $V_i$ に含まれていなければ:
      1. $V_i := \{v\}$ で更新。
      2. $v:0:i$ を他のすべての副官に送信。
   2. $i$ が $j_k$ から $v:0:j_1:\cdots:j_k$ 形式のメッセージを受信し、$v$ が $V_i$ に含まれていなければ:
      1. $V_i := V_i \cup \{v\}$ で更新。
      2. $k \lt m$ であれば副官はメッセージ $v:0:j_1:\cdots:j_k:i$ を、$j_1,\cdots,j_k$ を除くすべての副官に送信。
3. 各副官 $i$ がそれ以上メッセージを受信しなくなると ${\rm choice}(V_i)$ の値に従う。

${\rm choice}$ 関数は:

1. 集合 $V$ が単一の要素 $v$ のみで構成される場合 ${\rm choice}(V)=v$
2. ${\rm choice}(\emptyset) = {\rm RETREAT}$

要素が順序集合に由来する場合は $V$ の中央要素とする定義もあり得る。

定理 2. 任意の $m$ に対して、裏切り者が最大 $m$ 人であれば ${\rm SM}(m)$ はビザンチン将軍問題を解く。

署名なしのアルゴリズム ${\rm OM}(m)$ は $n \ge 3m+1$ が必要だが、署名ありのアルゴリズム ${\rm SM}(m)$ は $n \ge m+2$ で良い。

Missing Communication Paths

すべてのノードが互いに接続している完全グラフであるという仮定を外す。

定義 1

• (a) ノード $i$ に隣接するノード集合 $I=\{i_1,\ldots,i_p\}$ に含まれる各ノード $j \in I$ が $k \ne i$ である任意のノード $k$ への $i$ を経由しない経路 $\gamma_{j,k}$ を持っており、それらの経路 $\gamma_{j,k}$ がいずれも $k$ 以外に共通するノードを経由しないとき、$I$ は隣接の正規集合である。
• (b) すべてのノードの次数が $p$ であり隣接の正規集合を持つとき、グラフは $p$-正則である。

署名なしのアルゴリズム ${\rm OM}(m)$ を拡張して、$3m$-正則であれば $m$ 人の裏切り者がいてもビザンチン将軍問題を解決できるアルゴリズムにする。

アルゴリズム ${\rm OM}(m,p)$

1. 司令官に隣接する $p$ 人の副官の正則集合を $N$ とする。司令官は $N$ の副司令官それぞれに自身の値 $v$ を送る。
2. $N$ の各副官 $i$ について、$i$ が司令官から受信した値を $v_i$ とし、受信しなかった場合は RETREAT とする。副官 $i$ は $v_i$ を他のすべての副官 $k$ に送信する。
   1. $m=1$ のとき、定義 1 の (a) により存在が保証されている経路 $\gamma_{i,k}$ に沿って値を送信する。
   2. $m \gt 1$ のとき、将軍のグラフ $G$ から元の司令官を除去して得られる部分グラフで ${\rm OM}(m-1,p-1)$ の司令官として動作する。
3. $N$ の $i \ne k$ となる各副官 $i$ と各 $k$ に対して、ステップ 2 で副官 $k$ が副官 $i$ から受信した値を $v_i$ とし、値を受信しなかった場合は RETREAT とする。副官 $k$ は値 ${\rm majority}(v_{i_1},\ldots,v_{i_p})$ を使用する。

$p$-正則グラフから 1 つのノードを削除すると $(p-1)$-正則グラフとなる。$n=3m+1$ 構成のとき $3m$-正則グラフは完全グラフなので ${\rm OM}(m,3m)$ は ${\rm OM}(m)$ に縮退する。

定理 3. 任意の $m \gt 0$ と $p \ge 3m$ に対して、裏切り者が最大でも $m$ 人であればアルゴリズム ${\rm OM}(m,p)$ はビザンチン将軍問題を解く。

署名なしケースの証明は $3m$-正則であることを仮定している。しかもかなり強い接続正仮説である。

署名付きのケースでは、中継する裏切り者はメッセージを変更したり偽造することができないため、メッセージを中継しない動作しか行えない。つまり、忠実な将軍たちによってのみ形成される部分グラフが連結グラフであれば良い。

完全グラフ版のアルゴリズム ${\rm SM}(m)$ からの修正は「すべての副官に送信する」を「隣接するすべての副官に送信する」に変更するだけである。

定理 4. 任意の $m$ と $d$ に対して、裏切り者が最大でも $m$ 人であり、忠実な将軍の部分グラフの直径が $d$ であるとき、${\rm SM}(m+d-1)$ はビザンチン将軍問題を解く。

つまり、忠実な将軍の部分グラフが連結グラフであれば、${\rm SM}(n-2)$ は $n$ 人の将軍のビザンチン将軍問題を解くことができる。

${\rm SM}(m+d-1)$ は次の特徴を持つ。

1. 忠実な将軍のみを経由する最大 $d$ の長さの経路で結ばれた 2 つの忠実な将軍は同じ命令に従う。
2. 司令官が忠実であれば、忠実な将軍のみを経由する最大 $m+d$ の長さの経路で司令官と接続している忠実な副官は司令官の命令に従う。

Reliable Systems

多数決による高信頼システムを構築するためには:

1. 故障していないプロセッサはすべて同じ入力を使用しなければならない (従って同じ出力をする)。
2. 入力ユニットが故障していない場合、すべてのプロセッサはそれが提供する値を入力として使用する (従ってそれらは正しい値を生成する)。

これらは IC1, IC2 と同じである。要件 A1～A4 をメッセージパッシングシステムのケースに置き換えた説明が続く。

Conclusion

完全グラフでは ${\rm OM}(m)$ も ${\rm SM}(m)$ も最大 $m+1$ の長さの経路となり、$p$-正則グラフでは $m+d$ の長さの経路となる。${\rm OM}(m)$ と ${\rm SM}(m)$ は最大で $(n-1)(n-2)\cdots(n-m-1)$ 個のメッセージを使用するが組み合わせることでメッセージ数を削減できるかもしれない。

高コストだが恣意的な不正動作に対して信頼性を達成することは本質的に困難であるため仕方がない。故障の条件を緩和すればコストは削減できるが、スペースシャトルやミサイル防衛システムのような極めて高い信頼性が要求される場合はやはりコストがかかるだろう。