🧭

JavaScriptによる緯度経度と地図のXY(平面直角座標)との変換、および地理学入門

2022/11/11に公開

JavaScript

要約

緯度経度と地図上の平面直角座標(XY)とを変換するJavaScript関数を作成したのですが、そのプログラムの説明と、緯度経度と地図上の座標(XY)といった問題をを扱うのに最低限必要な「平面直角座標系」「世界測地系」「真北方向角」「XとYの向き」等の地理学の入門知識をまとめました。

■作成したJavaScript ( latlonxy.js ) の概要

地図表示用のWebフレームワーク(Leaflet等)のJavaScriptから呼出し可能な関数にして、座標変換計算の計算量の多い部分を事前計算して定数値にすることで軽量化しています。
緯度経度から地図上の平面直角座標(XY)に変換し、真北方位角、縮尺係数を算出します。
平面直角座標(XY)から緯度経度に変換します。

以下の図は、国土地理院「電子国土Web」のサーバーの東京の皇居周辺の地図をLeafletを使って表示し、latlonxy.jsで緯度経度と平面直角座標XYの相互変換をした例です。
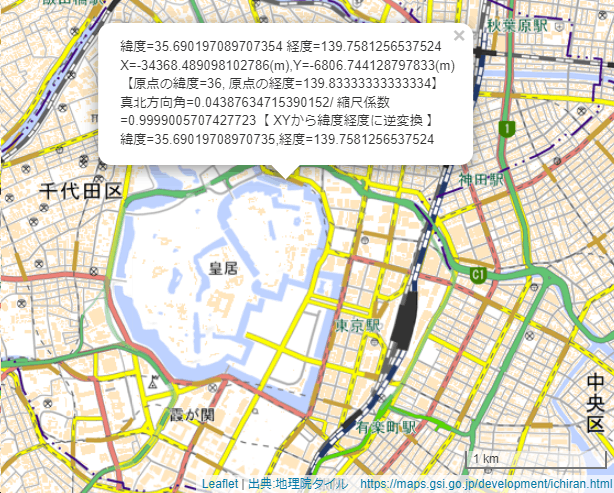
経度緯度をXY座標に変換して表示

地図をクリックした場所について、ポップアップで以下を表示しています。

1行目に緯度経度(Leafletで取得した値)
2行目にJavaScriptで変換した平面直角座標XY(m単位)
3行目に指定した系９の原点座標の緯度経度
４行目以降が、真北方向角、縮尺係数、および2行目のXYの座標値からJavaScriptで逆変換して緯度経度に計算し直した値です。

はじめに

現在は、国土交通省のProject PLATEAU(プラトー)のオープンな3Dの都市モデルや、国土地理院のデジタル地図(基盤地図情報)などの、高精度な日本の地図情報が簡単に使えるようになっています。また、Leaflet、TerriaJSなどのフレームワークを使用して、Webブラウザ上の2D, 3Dの地図上に緯度経度を指定することで簡単に図形や情報を追加表示できる便利な世界になりました。

一方、デジタル地図の位置情報は緯度経度なので、「緯度経度をXY座標で表示したい」「XY座標でメートル単位で作成した図や建物を地図上に表示したい」と思われた事があるかもしれません。

Web画面で入力すると緯度経度と平面直角座標を変換してくれるサイトは、国土地理院をはじめ、個人の方のサイトが幾つかあり、国土地理院の論文の中にもにもHTML画面で使用するJavaScriptの簡単なサンプルがあります。国土地理院の測量計算サイトではREST APIも提供していますが、時間当たりのAPI使用回数等の制限があります。自分のローカルで気兼ねなく地図用Webフレームワークを動作させているJavaScriptから関数呼び出しできて、グローバル変数を使わないで計算できるライブラリがあると便利です。そこで、このJavaScriptの関数プログラム「lanlotxy.js」を作成しました。

こうした緯度経度と地図上の座標(XY)の問題をプログラムで扱おうとすると、地理学の最低限の知識が必要になります。情報はネット上に豊富にあるのですが、情報が沢山の箇所にあるので、最低限の入門知識をまとめました。

座標変換計算式と関連情報

■「Gauss-Krüger 投影における経緯度座標及び平面直角座標相互間の座標換算についてのより簡明な計算方法: 2011 河瀬和重 (国土地理院時報，121，109–124．)」
この変換プログラムの変換計算式と真北方位角、縮尺係数計算式は、国土地理院の以下の論文記事が元になっています。この論文の中に簡単なHTML内で動作するJavaSciptも記載されていいます。

■「緯度経度と平面直角座標の相互変換を実装するための数式 : sw1227’s diary (Hatena blog)」
以下はsw1227さんが上記の論文をわかりやすく解説してくれた記事です。

■「緯度経度と平面直角座標の相互変換をPythonで実装する : sw1227 (Quiita)」
sw1277さんが作られた以下のPyhton版の変換プログラムです。

■　「国土地理院・測量計算サイト」
「平面直角座標への換算」と「緯度、経度への換算」の計算サービスを、Web画面指定、ファイルでの一括変換、REST APIの3通りの方法で提供しています。

座標変換に必要な地理学基礎知識

緯度経度とXY座標との変換を扱うには、最低限の知識として「世界測地系と日本測地系」、「平面直角座標系の１９個の系と原点」や、「XY座標の方向はどちら向きか」などを知らなければなりません。この章では、そうした基礎知識について説明します。こうした基礎をご存じの方は、この章は読み飛ばして『「latlonxy.js」実装』の章をご覧ください。

地理座標系(緯度経度の座標系)

「地理座標系」(Geographic coordinate system)とは、球体(正確には楕円体)である地球上の位置を緯度と経度で表現する座標系です。緯度が南北方向、経度が東西方向を表します。

赤道を緯度0度として、北側が北緯、南側が南緯と呼び、南北に0度～90度の範囲です。
ロンドンにあるグリニッジ天文台跡を通る南北の線を経度0度として、東周りを東経、西回りを西経と呼び、東西に0度～180度の範囲です。
南北の線を「子午線」と呼びます。地図上では子午線を「経線」と呼びます。

日本の位置は、東経122度～154度、北緯20度～46度の範囲になります。
「日本の東西南北端点の経度緯度」

「北」とは？

定義の元となる「北」は、地軸の北端(=北極点)であり「真北」（しんほく）と呼ばれます。これは磁石が指す「磁北」（じほく）とは差があります。場所によって磁北の方向は異なりますが、日本では真北よりも西に振れています。「北」は、これ以外にも平面の地図上では「座標北」もしくは「方眼北」と呼ぶ三番目の北が生まれます。これについては後ほど説明します。

https://www.gsi.go.jp/KIDS/KIDS11.html

参考: 「天の北極」とは地球の地軸を延長した方角にありますが、地球は約2万5800年周期で微妙に首(地軸)を振るため、「天の北極」やその近く(約0.6度ずれた場所)にある北極星はごく僅かづつですが常に動いて見えます。北極星は今は「こぐま座」にありますが、2000年前にはお隣の「りゅう座」にあったそうです。

緯度経度の表記方法

緯度経度の表記方法は複数ありますが、10進数か度分秒形式で表現されることが多いです。

10進法(例: 138.4305146388889)
度分秒形式で「度」「分」「秒」で区切る(例:138度25分49秒8257)
度分秒形式で「°」「'」「"」で区切る(例:138°25'49.8257")

なお、「°'"」形式の度分秒をデータ処理しようとすると、目視上は同じでも文字コードが異なる場合があります。これ以外も同じに見える別な文字があるかもしれませんのでご注意ください。付記している16進数はUTF-16の文字コードです。

分の表記：半角「'」(x27)(single-quotation)/ 全角「′」(x2032) / 全角「’」(x2019)
秒の表記：半角「"」(x22)(double-quotation)/ 全角「″」(x2033) / 全角「”」(x201D)

国土地理院、国交省、Googleなどのデジタル地理データでは緯度経度は10進数で表記されますが、様々な資料で度分秒で表記された場合も多いので、プログラムで値を使用するために10進数への変換方法を覚えておいてください。

度分秒表記「DDD度MM分SS秒XXX」から10進数表記「DEC」への変換

DEC = DDD + ( 1度未満の角度の秒表記 ) ÷ 3600秒
    = DDD + ( 60 × MM +  SS.XXX) ÷ 3600

例えば「138度25分49秒8527」をJavaScriptで変数degreeに設定するコードは以下になります。

let degree = 138 + (60*25 + 49.8527)/3600

「34度50分」を変数latitiudeに設定する場合は以下になります。

let latitude = 34 + 50/60

日本では緯度経度は「東経xx度、北緯yy度」の順番で表記されることが多いですが、世界的な標準や、デジタル地図データは「緯度、経度」の順です。３次元データの場合は「緯度、経度、標高」の順になります。

平面直角座標のXY座標

球形(正確には楕円体)の地球上の位置は緯度経度で表しますが、2次元平面の地図に投影してXYで表す座標系が投影座標系です。

■ 球体を平面に投影するイメージ図
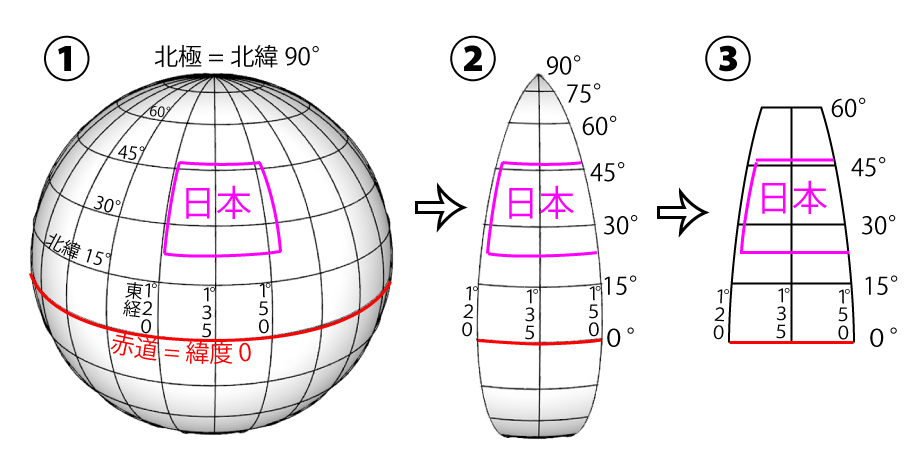
地球を平面に投影
上記は実際の投影法とは異なりますが、球体を平面にする様子を理解するためのイメージ図です。①の地球の表面を子午線(経度の線)に沿って「たまねぎの皮」のようにむいたのが②です。「地球儀表面の世界地図の印刷された紙をむく」と言った方がよいかもしれません。膨らんでいる②の一部を切り取って、押し潰して平らにしたのが③だと思ってください。丸い面を「押し潰して平ら」にすると形が微妙に変わり、その分歪みが出るのがイメージできると思います。

■ 平面直角座標の投影方法
投影方法は複数ありますが、日本で現在使用している平面直角座標は、「ガウス・クリューゲルの等角投影法」によるものです。これは地球の楕円体の扁平率と、楕円の長い方の半径(赤道半径)から数学的に計算できる投影方法です。

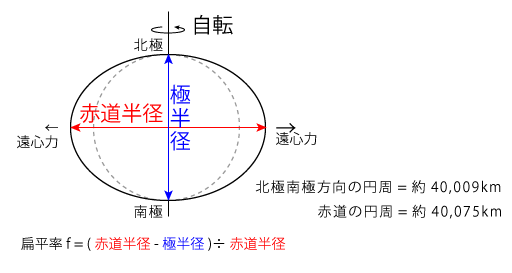
上記の模式図のように、地球は自転の遠心力によって赤道方向に膨らんだ楕円体です。(扁平率は、実際の計算では第三扁平率という、もっと複雑な式での計算値を使います。)

地球は球体ですので、地球上の広い範囲を平面上のXY座標に変換すると歪みがでます。例えば、メルカトル図法の世界地図は正角円筒図法ですが、世界を平面にするとロシア北部や北極近くでは東西方向に極端に拡大されて歪んでいるのが分ります。

経度(東西方向)は、赤道(緯度0度)上の1度は約111km(40,009km(赤道の円周) ÷ 360)ですが、北極点から1km離れた所では、経度1度は約17.4m (3.14km(=2π x 1km) ÷ 360)です。このように、経度(東西方向)の1度の距離は緯度(南北方向の位置)によって異なってきます。
緯度（南北方向）は、地球が完全な球体であれば経度の1度分の距離は地球上どこでも同じですが、実際には地球は楕円体です。そのため、緯度（南北方向）の1度の距離も、緯度によって僅かですが異なります。

日本の平面直角座標系

球体や楕円体を平面に投影する際に、狭い範囲に区切るほど歪みは小さくなります。日本では、平面直角座標のXYに変換した際の誤差が実用範囲でおさまるように、日本を19の系(領域)に分割して、分割した領域それぞれに原点(緯度経度で指定)を設けています。系は基本的に地球表面上の位置で分割されていますが、地図情報活用のために都道府県の境界上に系の境界が設定されています。

■ 日本の平面直角座標の1～19の系　 (原典:「わかりやすい平面直角座標系」 : 国土地理院)
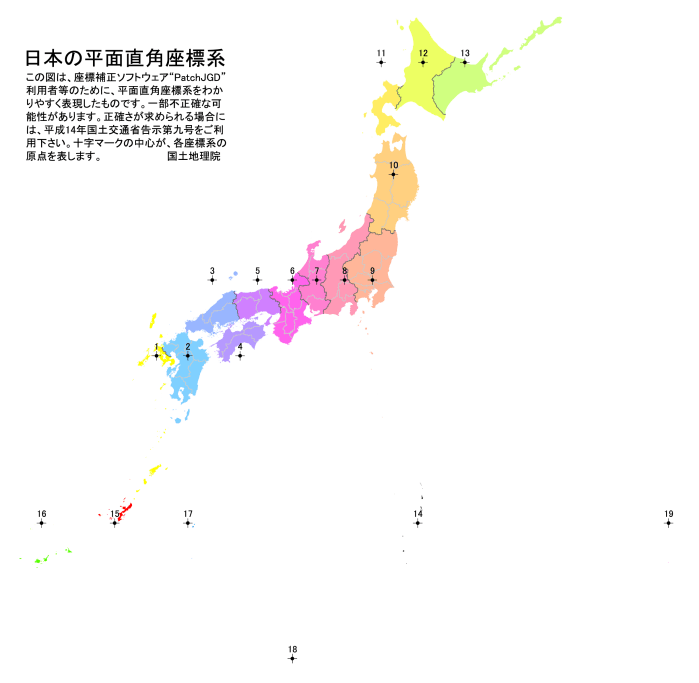
平面直角座標の領域と原点

■以下は上記の図の元資料です。「わかりやすい平面直角座標系」 : 国土地理院

■系1～系19の、該当する都道府県や地域と原点の緯度経度座標が以下に記載されています。「平面直角座標系（平成十四年国土交通省告示第九号）」

XとYの方向

地理学、測量、航海術の標準では、Xが南北方向(縦方向)、Yが東西方向(横方向)になります。
latlonxy.jsも、この標準にしたがっています。数学的なXYとは縦横が逆なので、混乱しないようにご注意ください。

X > 0 : 原点より北 / X = 0 : 原点上 / X < 0 : 原点より南
Y > 0 : 原点より東 / Y = 0 : 原点上 / Y < 0 : 原点より西

以下は具体的なイメージを持って頂くために、平面直角座標系の系９(関東圏)の地図の一部を図にしています。平面直角座標系は原点を中心としたXY座標系です。原点は緯度経度で指定され、この系9の場合は北緯36度0分0秒、東経139度50分50秒になります。
このように平面直角座標系は、19個の系それぞれが原点を持った座標系です。
関東圏のXY座標

上記図の左側にある、緑色をした縦のジグザグ曲線が系９と系８の境界です。これは県の境にそって設定されています。
平面直角座標系を緯度経度でスパッと直線的に切って系を決めてしまうと、一つの市、町や県の中に複数の系が複雑に入り組んでしまう箇所がでてきてしまいます。その状態では地方自治体でデータ活用をする上で不都合が起きるため、都道府県の境界に系の境界が設定されています。

系の境界は緯度経度で直線的に決まるるわけではないので、緯度経度から平面直角座標の変換には、必ず原点を指定してXY座標を計算する必要があります。
XY座標から緯度経度に変換するには、どこを原点としたXの値、Yの値であるか指定しないと計算できませんので、やはり原点を指定する必要があります。

測地系

緯度経度の値は、基準の取り方や測量方法によって異なってきます。それぞれの基準によって測量された緯度経度を「測地系」(Datum データム)と呼びます。現在の日本で使用している測地系は「日本測地系2011」で、世界標準である「世界測地系」に準拠しているので「世界測地系」とも呼ばれます。

日本での測地系は、明治時代の測量技術から進化して人工衛星やレーザーを使った測量技術になり、地震や噴火による地殻変動に対応したため、使用する測地系も進化させてきました。そのため、過去の測地系とは緯度経度の値が異なっています。

【日本測地系】(Tokyo Datum)
明治時代から2002年3月まで使用された測地系です。ベッセル楕円体を地球のモデルとして使用しています。「日本測地系」は、「旧測地系」「旧日本測地系」とも呼ばれます。
【日本測地系2000】(JGD2000)
測量技術向上と地殻変動を反映して改定された測地系で、2002年4月から2011年9月まで使用されました。日本測地系2000は、「ITRF：国際地球基準座標系」が定めた世界で共通に使用できる世界測地系に準拠しています。GS80楕円体を地球のモデルとして使用しています。
【日本測地系 2011 = 世界測地系】(JGD2011)
現在日本で使用している測地系です。測定基準は日本測地系2000と同じですが、20011年の東北大地震による大きな地殻変動後の測量に基づいており、2011年10月から使用されています。日本測地系2000の時点でも世界測地系に準拠していましたが、現在、日本国内の測地系で「世界測地系」と呼ぶ場合は「日本測地系2011」を指します。
ちなみに、東北大地震では牡鹿半島周辺で水平方向で5mを超える地殻変動があり、その後7年間の累積の地殻変動は牡鹿半島周辺で6mを超えています。

日本の測地系の切替えは、測量法の改定によって行われます。

「準拠楕円体」
地球は球形に近い赤道方向に膨らんだ楕円体なので、計算式で平面直角座標系に変換するためには、できるだけ実物の地球の形に近い数学的な楕円体の形状モデルを使用します。これを「準拠楕円体」と呼びます。どのような準拠楕円体に基づいて計算するかということも測地の基準に含まれます。

■日本の測地系の国土地理院の解説が以下にあります。「日本の測地系: 国土地理院」

■日本測地系 2011における、地震の影響による東日本、西日本の測量の違い、測量データの補正に関する説明にご関心があれば、以下がわかりやすいです。「日本測地系2011（JGD2011）とは : 空間情報クラブ」
https://club.informatix.co.jp/?p=998

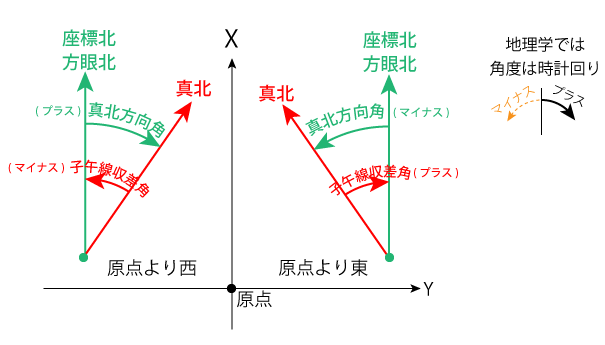
座標北(=方眼北)と真北方向角

地理学では角度は時計回りに表記されます。時計回りの角度はプラスの値、反時計回りの角度はマイナスの値で表記されます。

下記の図の左側は、「平面直角座標のXY座標」の「球体を平面に投影するイメージ図」を拡大したものです。経度の線上に真北(しんほく)がありますが、平面の地図上では真北の方向は地図に方眼を引いた時に、方眼線の真上方向にあるわけではありません。原点を通る地図の方眼の北だけが、真北と一致しています。地図の「方眼北」とは、平面直角座標のX軸方向(縦方向)のことであり「座標北」とも呼ばれます。
真北と座標北

この図では説明の都合上、平面直角座標の原点を東経135°においていますが、使用する平面直角座標の原点毎にこうした「座標北」（=方眼の北）と、真北の差があります。つまり、「北」の定義は「真北」と「磁北」に加えて、「座標北」の３つがあります。

平面直角座標の原点を通る子午線(経度線)上だけが、地図の「方眼の北」と「真北」が一致します。原点の東側では真北は座標北よりも西寄り、原点の西側では真北は座標北よりも東よりになります。

■「真北方向角」　座標北を基準にして、真北の(時計回りの)角度を「真北方向角」と言います。
■「子午線収納角」逆に真北を基準にして、座標北の(時計周りの)との間の角度を「子午線収納角」と言います。「真北方向角」と「子午線収納角」は、同じ意味のことを基準を反対にして見た角度です。角度の値のプラスマイナスが逆になります。

真北方向

■　国土地理院の下記の「平面直角座標への換算」のサイトでは、緯度経度と系を指定すると、XY座標とともに「真北方向角」を表示します。

例えば関東圏は平面直角座標の系番号９ですが、原点は千葉県の一番北の野田市にあります。原点から東西に離れるほど真北方向角の方角が大きくなります。

東京都庁は原点から西に約34.5km離れていますが、真北方向角は約+0.08度です。
富士山近くの三国山は原点から83km西にあり、真北方向角は約+0.53度です。

例えば、デジタル地図上に大きな3Dモデルを斜めに配置する際に、南の隅と北の隅を緯度経度で指定して配置すれば問題ありません。南の隅だけ緯度経度で指定して、建物の向きを地図上のXY方向から回転角度を指定して配置すると、それは方眼北で方向を指定したことになります。建物の向きを真北に対する角度で指定したかったのだとすると、真北方向角だけずれた配置になります。

■　「方向角」「方位角」
地理学の角度では、「方向角」「方位角」という紛らわしい言葉があります。

「方向角」は，座標北から時計回りの角度です。
「方位角」は，真北から時計回りの角度です。

縮尺係数

平面直角座標のXY座標は、原点から東西に離れるほど誤差を生じるので、それを補正するための係数が「縮尺係数」です。

以下は国土地理院の「平面直角座標」の「縮尺係数」の説明の図と文章を引用したものです。

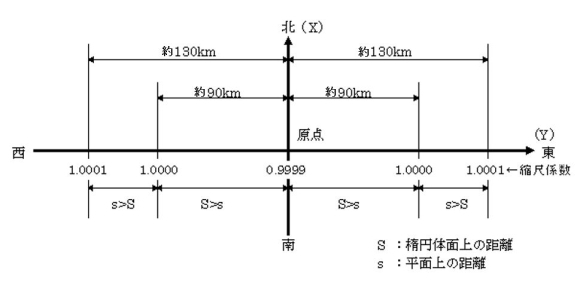
「距離については、原点から東西に離れるに従って平面距離が増大していくため、投影距離の誤差を相対的に1/10000以内に収めるよう座標原点を通る子午線上の縮尺係数を0.9999に設定し、かつ、座標原点から東西約130km以内を適用範囲とした座標系を設けています。」

原典: 「平面直角座標・縮尺係数の説明」：　国土地理院

「縮尺係数」は測量の世界でも奥深い、注意が必要な係数のようです。どういった注意が必要なののかは以下の「縮尺係数とエスバイエス（ｓ／Ｓ）はどう違う？」をご覧ください。「縮尺係数」は精度の高い作業のためには必要な係数ですが、正確に説明するのはかなり難しいようですので、縮尺係数については以上とさせて頂きます。

■　「縮尺係数とエスバイエス（ｓ／Ｓ）はどう違う？」: ATMSパーク

「latlonxy.js」実装

実装の概要

使用する関数は以下の4個です。

関数名	内容
latlon2xy	緯度経度から平面直角座標XYに変換し、真北方向角と縮尺係数を取得する
xy2latlon	平面直角座標XYから緯度経度に変換する
xyzone	任意の原点の緯度経度を指定して、その平面直角座標の座標系情報を取得
xyzonejapan	日本の平面直角座標系1～19の座標系情報を取得する

※　xy2latlon, lanlon2xyの「2」(two)は「to]の意味です。

座標系情報は「原点緯度、原点経度、定数S、定数A」の4つの要素を持つ配列です。定数S,定数Aは、原点位置に対応して計算された値です。

前述の論文の変換計算式は、三角関数、逆三角関数、双曲線関数、逆双曲線関数を多用した計算量が多いので「lanlotxy.js」は、地球の形状や平面直角座標系の19個の原点に依存する計算は事前に行って定数値として設定してしまい、計算量を最小限にしています。

関数の使用順序は以下の通りです。

zyzoneまたは xyzonejapan関数を最初に実行し、座標系情報を取得。
latlon2xy または xy2latlonを実行。

同じ系の座標変換を複数回する場合は、zyzoneまたは xyzonejapanは最初の1回だけ実行し、同じ座標系情報を使って、laton2xy, xy2latlonを使用します。

■ 日本の平面直角座標の系9を指定して、緯度経度から平面直角座標のXY座標に変換する例
zonejapan関数は、日本の平面直角座標の計算済みの定数を取得するだけなので、最も計算量が少なくなります。

//日本の平面直角座標の系9を指定し、原点と計算済みの定数を含む座標系情報を取得する
let zone = xyzonejapan(9);
//緯度35.6902°と経度139.7581°と座標系情報zoneを指定して、
//x,y座標と真北方向角、縮尺係数を取得する
let xy = latlon2xy(35.6902, 139.7581, zone);

let x = xy[0]; // x座標(=北方向。x>0が北、x<0が南)
let y = xy[1]; // y座標(=西方向。y>0が東、y<0が西)
let north = xy[2]; // 真北方向角(度)
let scaleFactor = xy[3]; // 縮尺係数

■　任意の緯度経度を原点に指定して、緯度経度から平面直角座標のXY座標に変換する例
zone関数は、指定された原点に対して、必要な定数を計算し、原点の緯度経度と共に定数を戻り値に設定します。

//緯度35.2°、経度138.0°を原点に設定し、定数を計算して座標系情報を取得する
let zone = xyzone(35.2, 138.0);
//緯度35.6902°と経度139.7581°と座標系情報zoneを指定して、
//x,y座標と真北方向角、縮尺係数を取得する
let xy = latlon2xy(35.6902, 139.7581, zone);

■　日本の平面直角座標の系9を指定して、平面直角座標のXY座標から緯度経度に変換する例

//日本の平面直角座標の系9を指定し、原点と計算済みの定数を含む座標系情報を取得する
let zone = xyzonejapan(9);
//X座標-34638.1とY座標-6806.74と座標系情報zoneを指定して、緯度経度を取得する。
let latlon = xy2latlon(-34638.1, -6806.74, zone);

let latitude  = latlon[0]; // 緯度
let longitude = latlon[1]; // 経度

JavaScriptのコードが変換計算式の資料のどこの実装なのか対応づけができるように、JavaScriptの変数名は、計算式の論文で使用しているギリシャ文字の英語読み、または短かすぎる場合は意味が想像できる変数名にしています。コメントの中に変換計算式中のギリシャ文字の変数名と計算式の一部を記載しています。

JavaScriptのコード

/**
 * latlonxy.js
 * 日本における世界測地系(=日本測地系2011)での、緯度経度と平面直角座標(XY)の双方向変換を行うJavaScript。
 * 以下の計算式に基づいて作成している。
 * Gauss-Krüger 投影における経緯度座標及び平面直角座標相互間の座標換算に
 * ついてのより簡明な計算方法: 2011 河瀬和重 (国土地理院時報，121，109–124．)
 * https://www.gsi.go.jp/common/000061216.pdf
 * 本プログラムは無保証であり、自己責任で使用すること。
 * author: Yuhichi Ishikawa (TonbiWing)
 */

/** 
 * 緯度経度から平面直角座標XYに変換し、真北方向角、縮尺係数と共に、4要素の配列を返す。
 * zone関数またはzoneJapan関数で作成した座標系情報(zone)を指定する必要がある。
 * 結果のx,yは地理学、測量、航海術の標準にしたがってxが南北(x>0が北、x<0が南)、yが東西(y>0が東,y<0が西)。
 * @param {number} latDegree 変換対象の緯度(度) (ϕ=latitude)
 * @param {number} lonDegree 変換対象の経度(度) (λ=longitude)
 * @param {number} zone 座標系情報 [緯度, 経度, 定数S, 定数A]の配列。
 * @return {number[]} [X座標(m単位), Y座標(m単位), 真北方向角、縮尺係数]の4要素の変数
 */
 function latlon2xy(latDegree, lonDegree, zone) {
    const originLat = zone[0]; //原点緯度(度)
    const originLon = zone[1]; //原点経度(度)
    const sOverline = zone[2]; //定数S
    const aOverline = zone[3]; //定数A

    function toRadian(degree) { return degree * Math.PI / 180; }
    function toDegree(radian) { return radian * 180.0 / Math.PI; }

    const coefN = 0.0016792203946287445; // N : 1/ (2F-1)
    const coef0 = 0.08181919104281579; // = 2√n/(1+n)
    const longerRadius = 6378137.0; //
    /** α(i) (i=1...,5) : 経度緯度から平面直角座標の変換(latlon2xy)に使う定数 */
    const alpha= [0.0, 8.377318247285465E-4, 7.608527848379248E-7, 
        1.1976455002315586E-9, 2.4291502606542468E-12, 5.750164384091974E-15 ];

    const lat = toRadian(latDegree);
    const lon = toRadian(lonDegree);
    const diffLon = lon - toRadian(originLon); //λ-λ0 　経度と原点の経度の差分
    const cosDiffLon = Math.cos(diffLon); //λc　= cos( λ - λ0) )
    const sinDiffLon = Math.sin(diffLon); //λs  = sin( λ - λ0) )  
    //t = sinh( atanh(sin((ϕ)　- 2√n/(1+n) * atanh(2√n/(1+n)*sin(ϕ))  )　
    const t = Math.sinh(Math.atanh(
              Math.sin(lat)) - coef0 * Math.atanh(coef0 * Math.sin(lat) ));
    const t_overline = Math.sqrt(1.0 + t*t); //t上線付 
    const xiDash = Math.atan(t / cosDiffLon); // ξ'
    const etaDash = Math.atanh(sinDiffLon / t_overline); // η'

    //平面直角座標XとYを計算するための行列式determinant	
    let determX = 0;
    let determY = 0;
    // tOverline, sigma, tauは子午線収差角γ (= -真北方向角) と 縮尺係数mのための変数
    const tOverline = Math.sqrt(1 + t*t);  	//t上線付 = √(1+t＾2)
    let sigma = 0; 	//σ (sigma) = 1 + Σ{j=1..5} 2jα(j) * cos(2jξ') * cosh(2j η')
    let tau = 0;  	//τ (tau) =  Σ{j=1..5} 2jα(j) * cos(2jξ') * cosh(2j η')

    for (let j = 1; j <= 5; j++) {
        let j2xiDash = 2*j* xiDash; //2j ξ'		
        let j2etaDash = 2*j* etaDash; //// 2j η'
        determX += alpha[j] * Math.sin(j2xiDash) * Math.cosh(j2etaDash);
        determY += alpha[j] * Math.cos(j2xiDash) * Math.sinh(j2etaDash);

        let j2Alpha = 2 *j* alpha[j]; // 2jα(j)
        //σ (sigma) = 1 + Σ{j=1..5}( 2jα(j) * cos(2jξ') * cosh(2j η')
        sigma += j2Alpha * Math.cos(j2xiDash) * Math.cosh(j2etaDash); 
        //τ (tau) =  Σ{j=1..5}( 2jα(j) * cos(2jξ') * cosh(2j η')
        tau += j2Alpha * Math.sin(j2xiDash) * Math.sinh(j2etaDash); 
    }
    sigma = sigma + 1;

    let result = [0,0,0,0]; // [x,y,真北方向角,縮尺係数]
    result[0] = aOverline * (xiDash + determX) -sOverline; //x
    result[1] = aOverline * (etaDash + determY); //y

    //γ (gamma 子午線収差角= -真北方向角)
    const gamma = Math.tanh( ((tau * tOverline * cosDiffLon) + (sigma * t * sinDiffLon)) 
        / ((sigma * tOverline * cosDiffLon) - (tau * t * sinDiffLon)) );
    const coefM = (1 - coefN) / (1 + coefN) * Math.tan(lat);  //m (scaleFactor)
    // m  (scaleFactor) = sOverline / a * √(σ^2 + τ^2)(t^2 + λx^2) {1+(1-n)/(1+n)*tanϕ)}^2 
    const scaleFactor = aOverline / longerRadius
        * Math.sqrt( (sigma*sigma + tau*tau)/(t*t + cosDiffLon*cosDiffLon) * (1 + coefM*coefM) );
    result[2] = toDegree(-gamma); //-γ (-gamma = 真北方向角)
    result[3] = scaleFactor; // m 縮尺係数
    return result;
}

/** 
 * 平面直角座標XYから緯度経度へ、系番号を指定して変換する。
 * 地理学、測量、航海術の標準にしたがってxが南北(x>0が北、x<0が南)、yが東西(y>0が東,y<0が西)。
 * zone関数またはzoneJapan関数で作成した座標系情報(zone)を指定する必要がある。
 * @param {number} x 変換対象のX座標 (原点からの南北の距離 (m単位))
 * @param {number} y 変換対象のY座標 (原点からの東西の距離 (m単位))
 * @param {number} zone 座標系情報 [緯度, 経度, 定数S, 定数A]の配列。
 * @return {number[]} 経度緯度(度単位)を示す1次元配列[緯度,経度]。
 */
function xy2latlon(x, y, zone) {
    const originLat = zone[0]; //原点緯度(度)
    const originLon = zone[1]; //原点経度(度)
    const sOverline = zone[2]; //定数S
    const aOverline = zone[3]; //定数A

    function toRadian(degree) { return degree * Math.PI / 180; }
    function toDegree(radian) { return radian * 180.0 / Math.PI; }

    /** β(i)　(i=1,2,...5) */
    const beta= [0.0, 8.377321681620316E-4, 5.905870211016955E-8, 1.6734826761541112E-10, 2.1648237311010893E-13, 3.79409187887551E-16 ];
    /** δ(i) (i=1,2,...6) */
    const delta= [0.0, 0.003356551485604312, 6.571873263127177E-6, 1.7646404372866207E-8, 5.3877538900094696E-11, 1.7640075159133883E-13, 6.056074055207582E-16 ];

    const xi = (x + sOverline) /aOverline; // ξ
    const eta = y / aOverline; // η
    // ξ'(xiDash)と η'(etaDash)を計算するための行列式determinant
    let determXi = 0;
    let determEta = 0;
    for (let j = 1; j<=5; j++) {
        //Σ{j=1..5}( βj * sin(2jξ)cosh(2jη) )
        determXi += beta[j] * Math.sin(2.0 * j * xi) * Math.cosh(2 * j * eta);
        //Σ(j=1..5){ βjcos(2jξ)sinh(2jη) }
        determEta += beta[j] * Math.cos(2.0 * j * xi) * Math.sinh(2 * j * eta);
    }
    const xiDash = xi - determXi; // ξ' 
    const etaDash = eta - determEta;	// η'
    const chi = Math.asin(  Math.sin(xiDash) / Math.cosh(etaDash) ); // χ= asin( sin ξ' / cosh η') 
		
    let sigmaLat = 0;
    for (let j = 1; j<= 6; j++) {
         sigmaLat += delta[j] * Math.sin(2.0 * j * chi); //Σ{j=1..5}( δjsin(2jχ) )
    }

    let latlon = [0, 0];
    ///緯度(radian単位)  ϕ = χ+ sigmaLat
    let latInRadian = chi + sigmaLat ;
    latlon[0] = toDegree(latInRadian) ;
		
    //経度(radian単位) λ = λ0+tan−1(sinh(η′)/cos(ξ′))
    let lonInRadian =  toRadian(originLon)
        + ( Math.atan(Math.sinh(etaDash) / Math.cos(xiDash)) );
    latlon[1] = toDegree(lonInRadian);
    return latlon;
}

/**
 * 任意の原点の経度緯度を指定して、平面直角座標系情報の配列(原点緯度、原点経度、定数S、 定数A)返す
 * @param {number} orgLat 原点の緯度
 * @param {number} orgLon 原点の経度
 * @return {number[]} 座標系情報 [緯度, 経度, 定数S, 定数A]の4要素の配列
 */
 function xyzone(orgLat, orgLon) {

    function toRadian(degree) { return degree * Math.PI / 180; }

    const orgLatRadian = toRadian(orgLat); // 経度をRadianに変換する 

    const scaleFm0 = 0.9999; // mo : 原点における縮尺係数
    const longerRadius = 6378137.0; //a: GRS80楕円体の長半径。
    const coefN = 0.0016792203946287445; // N : 1/ (2-楕円扁平率の逆数)
    const coef0=0.08181919104281579; //coef0 = 2√n/(1+n)
    /** A(i) (i=0,1...,5) : 経度緯度から平面直角座標と、その逆変換の両方に使う定数 */
    const largeA = [1.0000007049454078, -0.0025188297041239312, 2.6435429493240994E-6, 
        -3.4526259073074147E-9, 4.891830424387949E-12, -7.228726045813916E-15 ];

    //定数sOverLIneのための行列式 Σ(j=1..5)(Aj*sin(2*j*ϕ0) 
    let determS = 0;
    for (let j = 1; j <= 5; j++) {
        determS += largeA[j] * Math.sin(2.0 * j *  orgLatRadian);
    }
    // (m0*a)/(1+n)
    const originCoef = (scaleFm0 * longerRadius)  / (1.0 + coefN);
    // Sの上線付(ϕ0) = (m0*a)/(1+n) * ( A0 * ϕ0 + Σ(j=1..5)(Aj*sin(2*j*ϕ0) ) 
    const sOverline = originCoef * (largeA[0] * orgLatRadian + determS);
    // Aの上線付  = (m0*a)/(1+n) * A0
    const aOverline = originCoef * largeA[0];

    const result = [orgLat, orgLon, sOverline, aOverline];
    return result;
}

/**
 * 日本の平面直角座標系1～19の系番号を指定して座標系情報の配列 [緯度, 経度, 定数S, 定数A] を取得する。
 * 日本の系1～19の原点に対応した内部定数値を、事前計算済みの定数S,定数Aを取得することで、
 * 逆三角関数、双曲線関数などの計算を省略し、実行を軽量化する。
 * @param {number} sysno 系番号(1～19)
 * @return {number[]} [緯度, 経度, 定数S, 定数A]の4要素の配列
 */
 function xyzonejapan(sysno) {
    const origins = [
        [0.0,  0.0],    // 添字0は使用しない
        [33.0, 129.5],  // 座標系1: 長崎県 鹿児島県の後間、岩礁
        [33.0, 131.0],  // 座標系2: 福岡県　佐賀県　熊本県　大分県　宮崎県　鹿児島県（1系区域以外)
        [36.0, 132.16666666666667], // 座標系3:山口県　島根県　広島県
        [33.0, 133.5],  // 座標系4: 香川県　愛媛県　徳島県　高知県
        [36.0, 134.33333333333333], // 座標系5: 兵庫県　鳥取県　岡山県
        [36.0, 136.0],  // 座標系6: 京都府　大阪府　福井県　滋賀県　三重県　奈良県 和歌山県
        [36.0, 137.16666666666667], // 座標系7: 石川県　富山県　岐阜県　愛知県
        [36.0, 138.5],  // 座標系8: 新潟県　長野県　山梨県　静岡県
        [36.0, 139.83333333333333], // 座標系9: 東京都（14,18,19系以外)　福島県　栃木県　茨城県　埼玉県 千葉県　群馬県　神奈川県
        [40.0, 140.83333333333333], // 座標系10: 青森県　秋田県　山形県　岩手県　宮城県
        [44.0, 140.25], // 座標系11: 小樽市　函館市　伊達市　北斗市　北海道後志総合振興局の所管区域　豊浦町　壮瞥町　洞爺湖町
                        //          北海道渡島総合振興局の所管区域　北海道檜山振興局の所管区域
        [44.0, 142.25], // 座標系12: 北海道（11,13系以外)
        [44.0, 144.25], // 座標系13: 北見市　帯広市　釧路市　網走市　根室市　美幌町、津別町、斜里町、清里町、小清水町、訓子府町、
                        //           置戸町、佐呂間町、大空町　北海道十勝総合振興局の所管区域　北海道釧路総合振興局の所管区域　北海道根室振興局の所管区域
        [26.0, 142.0],  // 座標系14: 東京都のうち北緯28度から南であり、かつ東経140度30分から東であり東経143度から西である区域
        [26.0, 127.5],  // 座標系15: 沖縄県のうち東経126度から東であり、かつ東経130度から西である区域
        [26.0, 124.0],  // 座標系16: 沖縄県のうち東経126度から西である区域
        [26.0, 131.0],  // 座標系17: 沖縄県のうち東経130度から東である区域
        [26.0, 136.0],  // 座標系18: 東京都のうち北緯28度から南であり、かつ東経140度30分から西である区域
        [26.0, 154.0]   // 座標系19: 太平洋側最東端 南鳥島付近(東京都のうち北緯28度から南であり、かつ東経143度から東である区域)
        ];
    /**  参照論文の変数「Sの上付線」の平面直角座標系1～19毎の原点に対応した定数。latlon2xyとxy2latlonで共通 */
    const sOverline = [0 , 3652382.768270788, 3652382.768270788, 3985144.116029223, 3652382.768270788, 
        3985144.116029223, 3985144.116029223, 3985144.116029223, 3985144.116029223, 3985144.116029223, 
        4429086.077333566, 4873334.987359202, 4873334.987359202, 4873334.987359202, 2876546.889061122, 
        2876546.889061122, 2876546.889061122, 2876546.889061122, 2212145.0174775715, 2876546.889061122 ];
    /** 参照論文の変数「Aの上付線」の平面直角座標系1～19毎の原点に対応した定数。latlon2xyとxy2latlonで共通 */
    const aOverline = [0 , 6366812.400856472, 6366812.400856472, 6366812.400856472, 6366812.400856472, 
        6366812.400856472, 6366812.400856472, 6366812.400856472, 6366812.400856472, 6366812.400856472, 
        6366812.400856472, 6366812.400856472, 6366812.400856472, 6366812.400856472, 6366812.400856472, 
        6366812.400856472, 6366812.400856472, 6366812.400856472, 6366812.400856472, 6366812.400856472 ];

    const result = [ origins[sysno][0], origins[sysno][1], sOverline[sysno], aOverline[sysno] ];
    return result;
}

Leafletと共にlatlonxy.jsを使用した例

以下は本記事の冒頭の、東京の地図をクリックした場所の緯度経度、XY座標、原点の緯度経度、真北方向角、縮尺係数、をWebブラザーウエデポップアップ表示した画面を以下に掲載します。

経度緯度をXY座標に変換して表示

この地図表示にはフレームワークとしてLeafLetを使い、地図データは国土地理院の「地理院タイル」のサーバーから取得しています。以下に、表示用のHTMLを掲載します。

<!DOCTYPE html>
<html>
<head>
  <meta charset="UTF-8">
  <title>緯度経度と平面直角座標系XYとの変換デモ</title>
  <!-----Learletを使用して国土地理院の地理院タイルの地図データ上の緯度経度と平面直角座標の座標を表示するデモ----->
  <link rel="stylesheet" href="https://unpkg.com/leaflet@1.3.0/dist/leaflet.css" />
  <script src="https://unpkg.com/leaflet@1.3.0/dist/leaflet.js"></script>
  <!-- *********** latlonx.js を配置したPathを以下に指定する ***********************-->
  <script src="file:///D:/MyProgramData/GmlStudy/leaflet/latlonxy.js"></script>
  <script>
    function init() {

      //Leafletの初期化
      var map = L.map('mapcontainer', { zoomControl: false });
      map.setView([35.64, 139.7], 10);
      //Leafletの地図タイルのレイヤーに、国土地理院の地理院タイルの地図データのサーバーを指定
      L.tileLayer('https://cyberjapandata.gsi.go.jp/xyz/std/{z}/{x}/{y}.png', {
        attribution: "<a href='https://maps.gsi.go.jp/development/ichiran.html' target='_blank'>出典:地理院タイル　https://maps.gsi.go.jp/development/ichiran.html</a>"
      }).addTo(map);
      L.control.scale({ maxWidth: 200, position: 'bottomright', imperial: false }).addTo(map);
      L.control.zoom({ position: 'bottomleft' }).addTo(map);

    let popup = L.popup();
    map.on("click", (e)=>{
        //Leafletでクリックした地図の緯度と経度を取得
        let str = "緯度="+e.latlng.lat + " 経度=" + e.latlng.lng;

        //任意の緯度経度を原点として指定し、原点と原点に応じて計算した定数を含む座標系情報を取得する 
        let zone = xyzone(36.0, 139.83333333333333);
        //日本の平面直角座標の系9を指定し、原点と計算済みの定数を含む座標系情報を取得する
        zone = xyzonejapan(9);
        
        //緯度経度から平面直角座標系のxyに変換（xyの配列に[x,y,真北方向角,縮尺係数]が設定される。
        //xが南北、yが東西であることに要注意）
        let xy = latlon2xy(e.latlng.lat, e.latlng.lng, zone)

        str = str + " X=" + xy[0] + "(m),Y=" + xy[1]+"(m)"
        str = str + "【原点の緯度="+zone[0]+",  原点の経度="+zone[1]+"】"
        str = str + " 真北方向角="+xy[2]+"/ 縮尺係数="+xy[3]

        //変換したxyから再度、緯度経度の逆変換して元の緯度緯度に許容誤差内で確認する。
        //invLatLngの配列に[緯度,経度]が設定される。
        let invLatLng = xy2latlon(xy[0], xy[1], zone)
        str = str + "【 XYから緯度経度に逆変換 】緯度="+invLatLng[0]+",経度="+invLatLng[1]

        popup.setLatLng(e.latlng).setContent(str).openOn(map);
    });

    }
  </script>
</head>
<body onload="init()">
  <div id="mapcontainer" style="position:absolute;top:0;left:0;right:0;bottom:0;"></div>
</body>
</html>

画面右下には、「国土地理院コンテンツ利用規約」と地理院タイルの利用条件に従い、出典を明示し、地理院タイル一覧ページへのリンクをつけています。

Leafletについては「埼玉大学教育学部人文地理学・谷謙二研究室」の以下の「Leafletの使い方」の情報を参考にしています。

変換計算精度、データ精度と考察

本JavaScriptの変換プログラムにどの程度の計算精度があるのか、国土地理院の測量計算サイトの座標計算サービスが正しいものして、比較検証しました。

緯度経度から平面直角座標のXYに変換した結果でいうと、国土地理院の計算サービスではXY座標の表示する桁の最小単位は 0.1mmですが、比較テストの結果、1%の割合で最大0.2mm誤差がある場合がありました。
一つの系の任意の1点の緯度経度から平面直角座標のXYへの変換では、2倍の安全率をとると最大0.4mmの誤差があると考えます。これが許容される誤差範囲か否かは使用目的によります。

詳細は以下をご覧ください。XY座標の計算精度が1メートル単位で合っていれば問題無いという方や、緯度経度はGoogle Mapと同様に小数点以下6桁あれば十分という方は、この章は読み飛ばしてください。

変換結果の比較検証結果

国土地理院の測量計算サイトの座標計算サービスの変換結果が正しいものとすると、本JavaScript版の結果との誤差は以下の通りです。比較した点は1つの系について102地点で、原点から10Km、30Km、60Km、90Km、130Km離れた地点を選択しています。系2、系5、系9、系10、系12、系15の6か所の系で同様に比較テストをしました(合計612点の比較)が、系による誤差の差異はありませんでした。原点の東側と西側で対称な点を比較すると変換結果も対象なので、原点の東西間での誤差の差異はありませんでした。

■　データの種類別、小数点以下の表示桁数と、小数点以下の値の誤差
※1 国土地理院の座標変換サービスの、小数点以下の表示桁数
※2 国土地理院の値を正として、本プログラムの計算値が小数点以下の何桁目に差異があったかを示す
※3 緯度経度から変換した平面直角座標のXY座標の値
※4 平面直角座標のXY座標から変換した緯度経度の値
※5 原点を通る経線上(縦軸上)の３点のみ
※ 値の表記は、例えば小数点以下4桁目の値が1異なる(つまり0.0001の誤差がある)場合、「4桁目の誤差1」と表記します。
※　測量計算サイトのWeb画面上の表示桁数と、REST APIを使った場合の桁数は同じです。

値の種類	表示桁数※1	本プログラムの誤差※2
XY座標※3	4	97%が誤差0 / 2%が4桁目の誤差1=0.1mmの誤差 / 1%が4桁目の誤差2=0.2mmの誤差
緯度経度※4	9	1%が9桁目の誤差2 / 34%が9桁目の誤差1 / 65%が誤差 0
真北方位角	9	3%(※5)が9桁目の誤差0 / 61%が7桁目が1の誤差※5 / 35%が6桁目の誤差1 / 1%が6桁目の誤差2
縮尺経緯数	8	全て誤差0

※注1 : 実際のテストは6個の系で合計612点行いましたが、系が違っても原点からの相対位置が同じだとほぼ同じ結果になるので、結果からすると１つの系だけのテストでも同じでした。

誤差の原因と変換計算式

「国土地理院の測量計算サイトの座標計算サービス」の計算結果はどの程度の精度なのか、とその値と誤差が出る原因は何なのか考察しました。

■　変換計算式
本JavaScriptプログラムは国土地理院の論文記事「Gauss-Krüger 投影における経緯度座標及び平面直角座標相互間の座標換算についてのより簡明な計算方法」に基づいています。これは本来は無限個数の多項式の展開を、実用範囲の5項までで止めています。

一方、国土地理院の測量計算サイトの計算は、おそらくより複雑で精度の高い「精密測地網一次基準点測量計算式」に基づくものではないかと推測します。そう考える理由は、国土地理院が配布する座標変換のVBプログラムTKY2GDのソースコードの計算式が「精密測地網一次基準点測量計算式」で書かれており、多くのユーザーが利用する測量計算サイトは同等かそれ以上の精度で計算サービスを提供するため、同じ「精密測地網一次基準点測量計算式」か、更に精度の高い計算式を使用しているものと推測します。

■　誤差の原因
論文の計算式に基づいて著者が作成したJavaScript版とJava版とでは計算誤差は同程度でした。他の方が個人で作られた同じ計算式で作られたPython版、JavaScript版のプログラムで四つ試してみても計算誤差は同程度でしたので、OSや言語と逆双曲線関数計算ライブラリーの違い、多少の計算順序の違いによる誤差が原因ではないと考えます。
そうだとすると、範囲の原因としては、変換計算式の違いによって誤差が生じているのではないかと推測します。機会があれば国土地理院の方にこの点についてお聞きしてみたいところです。

参考：緯度経度データの精度

参考情報として、データの緯度経度情報の精度として、国土地理院の基盤地図情報と、国土交通省(Project PLATEAU)に記載された緯度経度データの精度をまとめてみました。日本の緯度は北緯20～46度の2桁、経度は東経122～154度の3桁ですので、緯度経度の小数部の桁数だけまとめました。

データソース	緯度経度の小数部桁数
基盤地図情報※1	9
City GML・bldg(建物)※2	13
City GML・tran(道路) ※2	14
City GML・DEM(地形)※2	15

※1 国土地理院・基盤地図情報
https://fgd.gsi.go.jp/download/menu.php

※2 国土交通省　Project PLATEAU オープンデータポータルサイト (City GML)

前出の論文による平面直角座標のXYと双方向変換の変換計算式を実装したプログラムは小数点以下9桁までが有効数字と考えられます。Project PLATEAU のCity GMLの桁数の多いデータは、これが本当ならば1ミクロン単位よりずっと高精度なので、実際の所どこまでがデータの有効数字なのかわかりませんが、いづれにしても非常に高精度です。

おわりに

Project PLATEAUの対談で、ハッカソン参加者の方々が平面直角座標系と緯度経度変換に苦労されたという記事を読んだのがきっかけで、このJavaScript版の変換プログラムを公開することにしました。個人で作られている変換プログラムは色々あるのですが、Web画面で入力するものや真北方位角や縮尺係数が無い場合が多かったので、ライブラリとして使えるようにしました。
本プログラムは無保証ですので、自己責任で自由にお使いください。もしもデジタル地図情報を活用する方々のお役に立てれば幸いです。

精度問題

計算精度の考察で書きましたように、XY座標の変換誤差は、テスト結果の2倍の安全率をとると最大0.4mmと考えます。例えば都市モデルに3Dの建物などの構造物を配置して、位置をすり合わせながら配置するように非常に高い精度が求められる場合、この精度で足りるのかはご確認ください。

複数の構造物のオブジェクト間の位置に精度を求められる場合は、外部の3Dツール上でのXYZ座標上で複数オブジェクトをくみ上げて配置してから、一つの大きな塊のモデルとして緯度経度に変換して配置するといった工夫が必要になるかもしれません。

「真北方向角」と精度の問題

基礎知識で説明した「真北」と「座標北」との角度差(真北方向角)も、大きな構造物を地図上に配置する場合などで高い精度を求める場合は気になる点です。例えば建物の一か所だけを、XY座標から緯度経度に変換し、2Dまはた3Dツール上で配置し、建物の向きをツール上で角度指定して回転させると、それは座標北に対する回転になります。回転させた建物は、真北方向角だけ向きに誤差を生じることになります。
真北方向角が問題になる精度を求めるのであれば、配置する構造物の２隅のXY座標を計算するなどといった工夫が必要でしょう。

今後の平面直角座標の系の変更への対応

現在の日本の平面直角座標の系は1～19ですが、以前は今よりも少なく、2010年に最終改定されて現在に至ります。今後、太平洋上の海底火山の噴火などで新しい島ができると、平面直角座標系の系が増えたり変更されるかもしれません。
本プログラムはJavaScriptの軽量化のために、2022年時点の平面直角座標の19個の原点に依存する計算を事前に行って定数にしていますが、原点の緯度経度を指定して計算する関数も用意しています。それでも計算の大部分を占める楕円体計算の定数化はされていて既に軽量化されていますので、系の原点が追加変更になってもlatlonxy.jsの変更なしに対応することができます。