Open2023/04/15にコメント追加2

Python controlで試す制御（主に状態制御）

0次ホールドと双一次変換の比較

【目的】
離散時間の制御器設計として，(1)連続時間の制御器を離散時間に変換する，(2)離散時間にした制御対象を用いて制御器を設計する，のアプローチがある．
(1)の変換としていくつかある中の 0次ホールド，双一次変換したブロックの応答を連続時間と比較，Python controlでの実現

【ref】制御系設計論 14章

１次遅れな制御器を考える．

K_c = \frac{1}{s+1}

状態方程式だと

\begin{aligned} \dot{x}(t) &= -x(t) + u(t) \\ y(t) &= x(t) \end{aligned}

つまり $A=-1,B=1,C=1,D=0$

0次ホールドで離散時間(サンプリング $t_s$ )にすると

\begin{aligned} A_d &= e^{At_s} = e^{-t_s} \\ B_d &= \int^{t_s}_0 e^{At} dt B = 1-e^{-t_s} \\ C_d &= C = 1 \\ D_d &= D = 0\\ \end{aligned}

双一次変換だと

\begin{aligned} A_d &= (I+\frac{t_s}{2}A)(I-\frac{t_s}{2}A)^{-1} = \frac{1}{3} \\ B_d &= \frac{t_s}{2}(I-\frac{t_s}{2}A)^{-1} = \frac{1}{3} \\ C_d &= C(A+I) = \frac{4}{3} \\ D_d &= CB+D = \frac{1}{3} \\ \end{aligned}

Python controlの場合

from control.matlab import *
import numpy as np
import matplotlib.pyplot as plt

# 0次ホールド
ad = np.exp(-dt)
bd = 1-np.exp(-dt)
cd = 1
dd = 0
dt = 1
sys0 = ss(ad,bd,cd,dd,dt)

# 双一次
ad = 1/3
bd = 1/3
cd = 4/3
dd = 1/3
dt = 1
sys1 = ss(ad,bd,cd,dd,dt)

# プロット
n = 10
t = np.arange(n)*dt
x0 = 0
y1,t = step(sys1,t,x0)
y0,t = step(sys0,t,x0)

# 連続時間
sysid = tf([1],[1,1])
tid = np.arange(100)*0.1
yid,tid = step(sysid,tid,x0)

## whereを入れないと後の値を前に引き伸ばすのでホールドっぽくならない
plt.step(t,y0,where='post',label="zero-hold") 
plt.step(t,y1,where='post',label="bilinear")
plt.plot(tid,yid,label="continuous")
plt.legend()

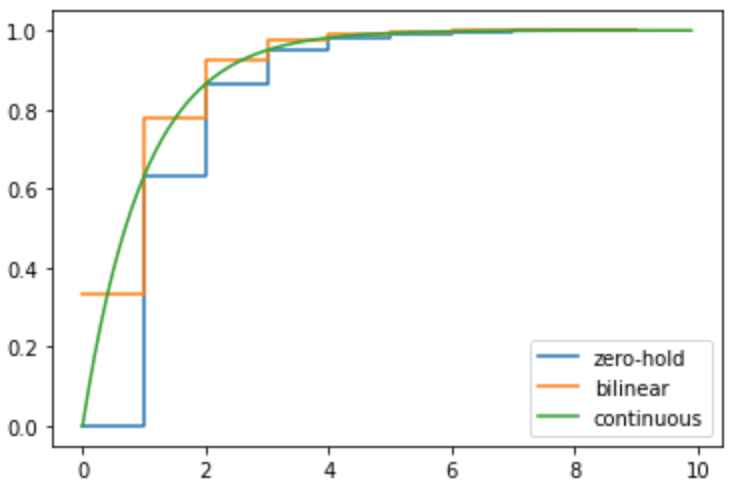
graph

0次ホールドは連続時間の応答のサンプリングタイミングの値をホールドする（定義のまま）
双一次は平均的に近い値になる．遅れない = 位相の周波数特性が連続時間に近くなるのに対応しているっぽい．

連続時間のsysをc2dで離散化してももちろん同じ結果になる．

tomkim

離散時間のフィードバック制御器により安定化

【目的】
極配置で設計したフィードバック制御器でどのように安定化されるかのチェック

【ref】制御系設計論 14章演習14-7

{\bf x}[k+1] = A_d {\bf x}[k] + B_d u[k] \\ {\rm where} \ A_d = \begin{bmatrix} \frac{1}{2} & 1 \\ 0 & 1 \end{bmatrix} , \ B_d = \begin{bmatrix} 0 \\ 1 \end{bmatrix}

安定性は $A_d$ の固有値が $0.5, 1$ と絶対値1未満ではないため安定ではない(0に収束しない)

# もとの制御対象
ad = np.array([[0.5,1],[0,1]])
bd = np.array([[0],[1]])
cd = np.array([[1,0],[0,1]])
dd = np.array([[0],[0]])
dt = 0.1
sysdef = ss(ad, np.zeros([2,1]), cd, dd, dt) # uに入力したいわけではないため zeros
n = 50
t = np.arange(n)*dt
x0 = [0.3,0.2]
y0,t = step(sysdef,t,x0)
plt.step(t,y0[:,0,0],where='post',label="x1")
plt.step(t,y0[:,1,0],where='post',label="x2")
plt.legend()

安定化前

$F=[f_1 f_2]$ を用いて状態フィードバックする場合，固有方程式は

\left| \lambda I - (A_d + B_d F ) \right| = \lambda^2 - \left(f_2+\frac{3}{2}\right)\lambda + \left(\frac{1+f_2}{2} - f_1 \right) = 0

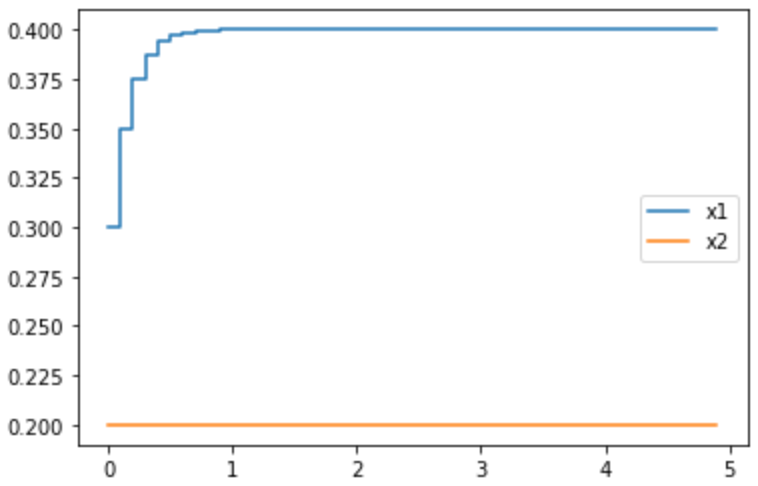
極配置を $\{0,0\}$ とすると， $f_1 = -\frac{1}{4}$ , $f_2 = -\frac{3}{2}$ と求まる．

f = np.array([[-1/4, -3/2]])
sysfb = ss(ad+bd@f, np.zeros([2,1]), cd, dd, dt)
y1,t = step(sysfb,t,x0)
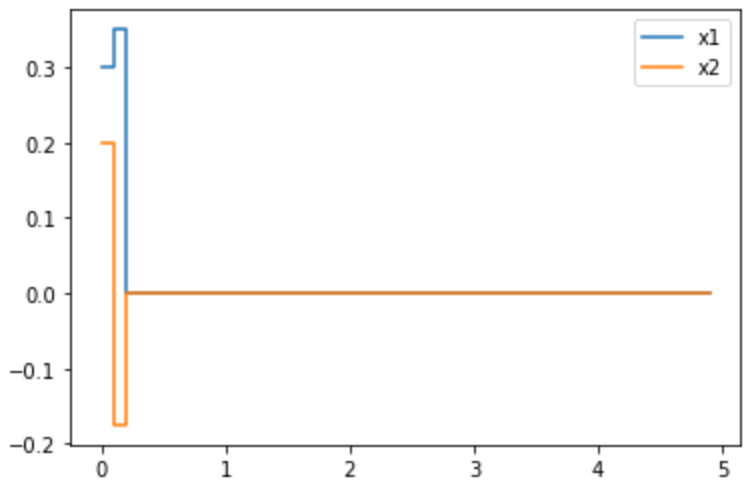
plt.step(t,y1[:,0,0],where='post',label="x1")
plt.step(t,y1[:,1,0],where='post',label="x2")
plt.legend()

安定化後