Pythonで試す偏微分方程式

例えば2次元の熱の伝達は次のような拡散方程式で記述できる．

\frac{\partial T}{\partial t} = \alpha \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} \right)

こういった物理モデルを強化学習のシミュレーション環境に取り込むべく，まずはPythonで数値解析できるところまで取り組んでみた．パッと探した限りでは拡散方程式（偏微分方程式）をPythonで数値解求めるようなライブラリは見つからず，大体直接書き下していたため，ここではライブラリを使わず求める方法について記載する．

陰解法とヤコビ法、ガウス=ザイデル法 | 科学技術計算講座3-6 | 科学技術計算ツール
こちらのページによると， 解の出し方として大きく2つに分かれる．

• 前期を右辺に入れて次の期の差分が出てくる陽解法
• 連立させ，1期ごとに何度も計算して収束させながら求める陰解法

陽解法は早く求まるが，CFL(Courant-Friedrichs-Lewy)条件 \Delta t \le \frac{\Delta x^2}{2\alpha}を満たさないと計算更新が伝わるより早く時間が過ぎてしまい安定解が出せない問題がある．刻み時間を大きくしたい，メッシュを細かくしたい場合には陰解法を使う．
陰解法にも種類があるようだが，ページに記載されている，更新された値を次々使う「ガウス=ザイデル法」で求める．

２次元熱伝導方程式のシミュレーション | 科学技術計算講座3-10 | 科学技術計算ツール
こちらにガウス=ザイデル法で求めるコード例が記載されており，もう少し一般化させたクラスを作成してみた．

上部に温度一定領域があり，二次元の熱拡散をシミュレーションしてみた．x方向の温度プロファイルの時間変化は次のようになる

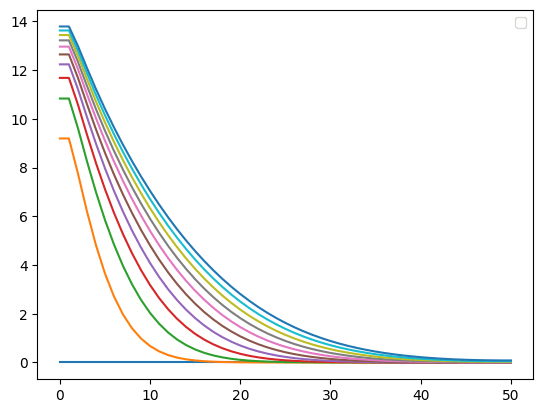
また温度分布をアニメーションにするとこんな感じ

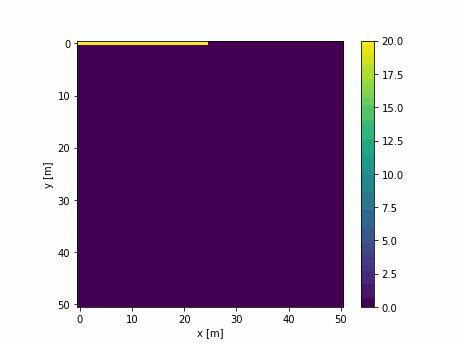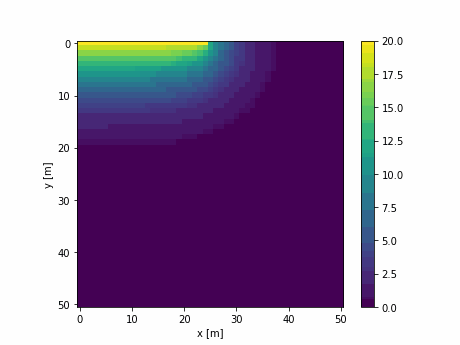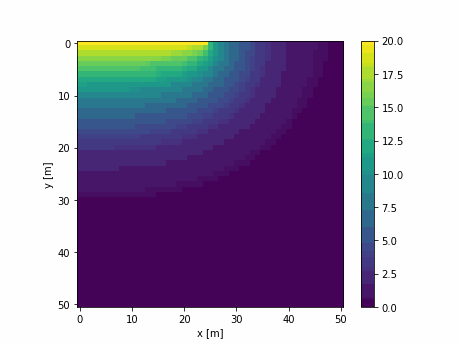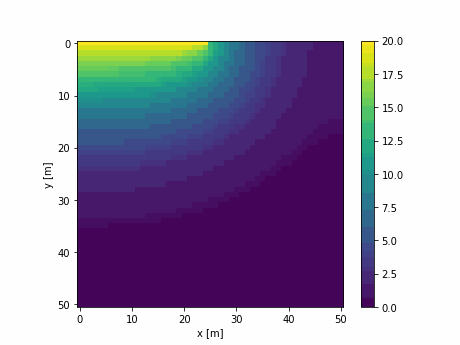
y方向の拡散係数を0として，y方向のサイズを3以上にすれば1次元の拡散もシミュレーション可能．
alpha[2]の比例項に負の値を入れれば熱の逃げが表現できる．