Python Controlを用いたVRFTによるPID制御器設計

はじめに

VRFT (Virtual Reference Feedback Tuning) は，制御対象のモデルが不明であっても，制御対象の入出力データから直接制御器を設計できる手法です．
本ノートは，参考記事を下敷きに，規範モデルの違いや制御器側が違う場合にPython Controlを用いてVRFTを構成する例を示します．

参考記事

1. Pythonによるデータ駆動制御VRFTによるPID制御器オートチューニング #データサイエンス - Qiita

備考

• 私は制御の基礎知識はありますがVRFTは初学です．説明で曖昧な点・不正確な点があるかもしれませんがご容赦ください．
• VRFT自体の実装については記事1記載の内容を使わせていただきました．著者に感謝いたします．
• 制御系が線形の場合のみを扱っています．非線形の場合は最適化を使う必要があり，本ノートでは扱いません．

VRFTの概要

    +
r --> ○ --> [C] --> u --> [P] ┯-> y
    - ^                       |
      └-----------------------┘ 

上図のような制御系を考えます．$r$が目標値，$y$が制御対象$P$の出力，$u$が制御入力，$C({\bf \theta})$が制御器，$\bf \theta$は制御器のパラメータとします．
$P$が未知な状態で，$C$と$P$からなる閉ループ系で$T_d$という規範モデルを実現したいとします．

なんらかの$r$(例えばステップ信号)を入れた場合に，制御機出力が$u_0$，制御対象出力が$y_0$となったとします．

プレフィルタを$L$とおくと，次の評価関数を最小化する$\bf \theta$を求めることがVRFTの目的です．

$$J({\bf \theta}) = \left\|Lu_0 - C({\bf \theta})\frac{1-T_d}{T_d}Ly_0\right\|^2$$

参考記事1.では，制御器$C$が以下のようなPID制御器の場合を考えています．

$$C = K_i\frac{1}{s} + K_p + K_d\frac{s}{\eta s+1}$$

ただし，微分器は不完全微分を用いています．

$J$の第2項を展開すると，

$$\begin{align} C\frac{1-T_d}{T_d}Ly_0 &= \left(K_i\frac{1}{s} + K_p + K_d\frac{s}{\eta s+1}\right)\frac{1-T_d}{T_d}Ly_0 \\ &= K_i\left(\frac{1-T_d}{sT_d}Ly_0\right) + K_p\left(\frac{1-T_d}{T_d}Ly_0\right) + K_d\left(\frac{s}{\eta s+1}\frac{1-T_d}{T_d}Ly_0\right) \\ &= K_i\phi_1 + K_p\phi_2 + K_d\phi_3 \end{align}$$

${\bf K}=[K_i, K_p, K_d]$，${\bf \phi}=[\phi_1, \phi_2, \phi_3]^T$とおくと，

$$J=\|Lu_0 - {\bf K}{\bf \phi}\|^2$$

と表せるため，$\bf \phi$の擬似逆行列$\bf \phi^+$を使えば，

$${\bf K} = Lu_0{\bf \phi}^+$$

のとき，$J$が最小(理想的には0)となります．

Pが1次遅れ系の場合 (参考記事通り)

共通部分

import numpy as np
import control as ct
from control.matlab import step, lsim
import pandas as pd
import matplotlib.pyplot as plt

# プラントがP，通常FB部がC1，先行部(後で使う)がC2として，tの時間系列に対してシミュレーションを行う
def sim(P,C1,C2,t):
  sys = ct.feedback(P,C1+C2) * C1
  y, _ = step(sys,t)
  u1, _, _ = lsim(C1,1-y,t)
  u2, _, _ = lsim(C2,-y,t)
  return u1+u2,y

def plot(t,u,y,m):
  fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(8, 8))
  ax1.plot(t,y,label='y')
  if m is not None:
    ax1.plot(t,m,"--",label='model')
  ax1.legend()

  ax2.plot(t,u,label='u')
  ax2.legend()

  plt.show()
  
# 標準のpid要素
def pidsys(kp, ki, kd, delta=0.05):
  C = ct.tf([kd+delta*kp,kp+delta*ki,ki],[delta,1,0])
  return C

# 何も通さないシステム
zerosys = ct.tf([0],[1])

調整前の特性

P = ct.tf([1],[3,1])
C = pidsys(1,1,0)
t0 = np.arange(100)*0.1
u0,y0 = sim(P,C,zerosys,t0)
plot(t0,u0,y0,None)

VRFTの実装

def vrft(u,y,t,Td,L=None,pid=False,delta=0.05):
  """
  Args:
    u: 制御器出力
    y: プラント出力
    t: 時間系列
    Td: 規範モデル
    L: プレフィルタ(指定しなければTdを使用)
  """
  if L is None:
    L=Td

  intg=ct.tf([1],[1,0]) # 積分
  dif=ct.tf([1,0],[delta,1])# 微分

  (y1p, T1p, x1p )=lsim(L*(1-Td)/Td,y,t)# P制御擬似誤差
  (y1i, T1i, x1i )=lsim(L*intg*(1-Td)/Td,y,t) # I制御擬似誤差
  (y1d, T1d, x1d )=lsim(L*dif*(1-Td)/Td,y,t) # D制御擬似誤差
  (y2a, T2a, x2a )=lsim(L,u,t)

  if pid:
    A=[y1p,y1i,y1d] # PID制御の場合   
  else:
    A=[y1p,y1i] # PI制御の場合

  invA=np.linalg.pinv(A) #擬似逆行列
  rho=y2a@invA #最適パラメータの求解
  return rho

時定数T=0.5の1次遅れ系を規範モデルとしてVRFTでパラメータを推定します

Ts = 0.5
Td = ct.tf([1],[Ts, 1])
[kp,ki,kd] = vrft(u0,y0,t0,Td,pid=True)
print(kp, ki, kd)
# 出力: 5.996377353160479 2.000370577548334 0.0019507285251812029

調整後の特性

C = pidsys(kp,ki,kd)
t = np.arange(100)*0.1
u,y = sim(P,C,zerosys,t)
m,_ = step(Td,t)
plot(t,u,y,m)

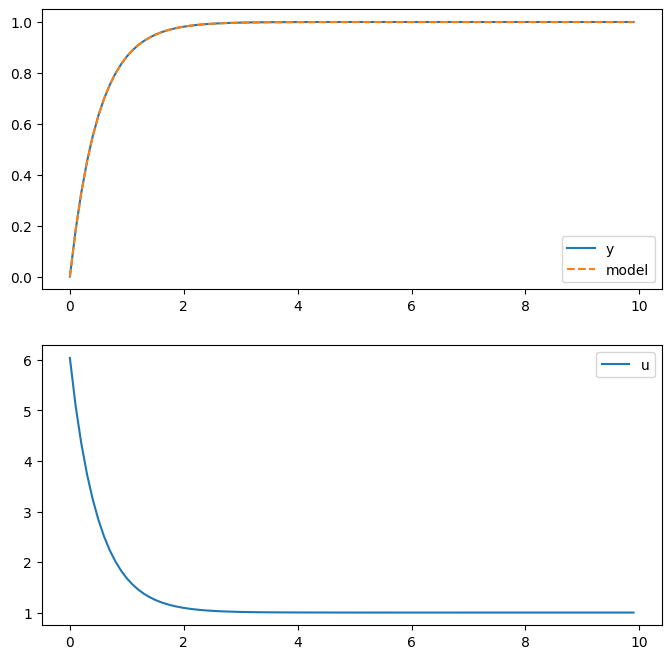
モデル通りの特性になっています

Pが2次遅れ系の場合

$$P=\frac{1}{s^2+s+1}$$

調整前

P = ct.tf([1],[1,1,1])
C = pidsys(1,1,0)
t0 = np.arange(100)*0.1
u0,y0 = sim(P,C,zerosys,t0)
plot(t0,u0,y0,None)

調整後

Ts = 0.5
Td = ct.tf([1],[Ts, 1])
[kp,ki,kd] = vrft(u0,y0,t0,Td,pid=True)
print(kp, ki, kd)
C = pidsys(kp,ki,kd)
t = np.arange(100)*0.1
u,y = sim(P,C,zerosys,t)
m,_ = step(Td,t)
plot(t,u,y,m)
# 出力: 1.8242034986971774 2.011911776796819 2.083319701519799

1次遅れにはならないのでズレるが，概ね規範モデルに近い特性になっています．ただし微分キックの影響で制御器出力がかなり高いです．

外乱に対する応答

外乱dがuに加わる場合，dからyの閉ループ伝達関数を考えれば良い．

$$G_{yd} = \frac{P}{1+P(C_1+C_2)}$$

def sim_disturb(P,C1,C2,t,amp=1):
  # 外乱はampの高さで矩形波的な特性とする
  sys = ct.feedback(P,C1+C2,-1) # Gydと同じものが得られる
  # 外乱系列を作成
  d = np.zeros_like(t)
  n = len(t)
  d[1:n//2] += amp
  y, _, _ = lsim(sys,d,t)
  u, _, _ = lsim(C1+C2,-y,t)
  return u,y,d

P = ct.tf([1],[1,1,1])
C = pidsys(kp,ki,kd) # 先ほどのVRFTで得た制御器
t = np.arange(200)*0.1
u,y,d = sim_disturb(P,C,zerosys,t)
plot(t,u,y,d)

少しオーバーシュート，アンダーシュートはあるものの，問題なく抑制できている．時定数も規範モデルに近い．

先行型PIDの場合

通常のFB側を$C_1$，先行側を$C_2$とします．

    +              +
r --> ○ --> [C1] --> ○ --> u --> [P] ┬-> y
    - ^            - ^               |
      |---> [C2] ----┘               |
      |                              |
      └------------------------------┘

評価関数は

$$J({\bf \theta}) = \left\|Lu_0 - \left( C_1\frac{1-T_d}{T_d} - C_2 \right) Ly_0\right\|^2$$

より ${\bf \phi}=[\phi_1, \phi_2, \phi_3]^T$ で

$$\begin{align} \phi_1 &= \frac{1-T_d}{sT_d}Ly_0 \\ \phi_2 &= \frac{1-T_d}{T_d}Ly_0 \\ \phi_3 &= -\frac{s}{\eta s+1}Ly_0 \\ \end{align}$$

と計算すれば同様にパラメータを算出できます．

D先行型(PI-D)でPが2次遅れ系の場合

def vrft_pi_d(u,y,t,Td,L=None,pid=False,delta=0.05):
  """
  Args:
    u: 制御器出力
    y: プラント出力
    t: 時間系列
    Td: 規範モデル
    L: プレフィルタ
  """
  if L is None:
    L=Td

  intg=ct.tf([1],[1,0]) # 積分
  dif=ct.tf([1,0],[delta,1])# 微分

  (y1p, T1p, x1p )=lsim(L*(1-Td)/Td,y,t)# P制御擬似誤差
  (y1i, T1i, x1i )=lsim(L*intg*(1-Td)/Td,y,t) # I制御擬似誤差 
  (y1d, T1d, x1d )=lsim(-L*dif,y,t) # D制御擬似誤差
  (y2a, T2a, x2a )=lsim(L,u,t) #

  if pid:
    A=[y1p,y1i,y1d] # PID制御の場合   
  else:
    A=[y1p,y1i] # PI制御の場合

  invA=np.linalg.pinv(A) #擬似逆行列
  rho=y2a@invA #最適パラメータの求解
  return rho

P = ct.tf([1],[1,1,1])

kp = 1
ki = 1
kd = 0
C1 = c_p(kp) + c_i(ki)
C2 = c_d(kd)

t0 = np.arange(100)*0.1
u0,y0 = sim(P,C1,C2,t0)
plot(t0,u0,y0,None)

調整後

Ts = 0.5
Td = ct.tf([1],[Ts, 1])
[kp,ki,kd] = vrft_pi_d(u0,y0,t0,Td,pid=True)
print(kp, ki, kd)
C1 = c_p(kp) + c_i(ki)
C2 = c_d(kd)
t = np.arange(100)*0.1
u,y = sim(P,C1,C2,t)
m,_ = step(Td,t)
plot(t,u,y,m)
# 出力: 43.490597529093534 2.0119117767967767 20.833197015198152

同様に規範モデルに近い特性となっています．微分キックがない代わりにPゲインが非常に大きいようです．

P = ct.tf([1],[1,1,1])
C1 = c_p(kp) + c_i(ki)
C2 = c_d(kd)
t = np.arange(200)*0.1
u,y,d = sim_disturb(P,C1,C2,t)
plot(t,u,y,d)

$C_1$に微分要素が入っていなかったことで，PIDで最適化した場合と外乱応答がかなり異なっています．

制御器出力に制限がある場合

加熱だけできる温度調整など，制御器出力に制限がある場合を考えます．ただ，制御器が非線形だと最小二乗法での最適化計算ができないため，制御器の最終段にある飽和器をプラント側の入力段にあるとみなすことで，擬似的に線形系として扱います．

    +              +
r --> ○ --> [C1] --> ○ --> u --> [Psat] --> [P] ┬-> y
    - ^            - ^                          |
      |---> [C2] ----┘                          |
      |                                         |
      └-----------------------------------------┘

$$P' = P \circ P_{sat} \\ P_{sat} = \text{saturation}(u_{min}, u_{max})$$

Controlライブラリでは*が直列接続に対応しており，非線形要素でも扱えます．

def sat_upd(t, x, u, params):
    return 1

def sat_out(t, x, u, params):
    return np.clip(u, params['u_min'], params['u_max'])

# 出力範囲が0~10の制御器の飽和要素
params = {'u_min': 0, 'u_max': 10}
P_sat = ct.nlsys(sat_upd, sat_out, states=1, inputs=1, outputs=1, params=params, name="SaturatedPlant")
print(P_sat)

P = ct.tf([1],[1,1,1])
C = pidsys(1,1,0)
t0 = np.arange(100)*0.1
u0,y0 = sim(P*P_sat,C,zerosys,t0)
plot(t0,u0,y0,None)

def sim(P,C1,C2,t):
  sys = ct.feedback(P,C1+C2) * C1
  y, _ = step(sys,t)
  u1, _, _ = lsim(C1,1-y,t)
  u2, _, _ = lsim(C2,-y,t)
  return u1+u2,y

Ts = 0.5
Td = ct.tf([1],[Ts, 1])
[kp,ki,kd] = vrft(u0,y0,t0,Td,pid=True)
print(kp, ki, kd)
C = pidsys(kp,ki,kd)
t = np.arange(100)*0.1
u,y = sim(P*P_sat,C,zerosys,t)
m,_ = step(Td,t)
plot(t,u,y,m)
# 出力: 1.824204210081015 2.0119118016594393 2.083319504953099

出力が10に制限されているので，本来最初期に40近くまで上がる制御器出力が抑えられ，規範モデルよりも遅い特性になっていることがわかります．

us, _, _ = lsim(P_sat,u,t)
plt.plot(t,u, label='u')
plt.plot(t,us, label='us')
plt.legend()
plt.ylim(-1,11)
plt.show()