🐧

MCP-Mod法の説明とRのDoseFindingパッケージの使い方

2024/04/07に公開

MCP-Mod法とは

ある変数 $X$ と $Y$ がどのような関係にあるか（ $X$ について $Y$ の平均がどのように変わるかの曲線）を知りたいとします。例えば、アンケートの報酬額 $X$ とアンケートの回答数 $Y$ 、薬の用量 $X$ と効果 $Y$ 、Webページのレスポンス速度 $X$ と離脱した人数 $Y$ などです。

MCP-Mod法はこれから実験をして $X$ と $Y$ のデータを取得し、用量反応関係（ $X$ が変われば $Y$ の平均も変わる関係）があるかどうかを多重検定し、その後で有意だったモデルたち（曲線たち）のどれに従いそうかモデル選択まで行う手法です。MCPはMultiple Conparison Procedureの略で、ModはModelingの略です。

モデルの候補たちは実験前に用意します。比較的シンプルな曲線を想定しています（例えば、一次関数、二次関数、指数関数、ロジスティック関数など）。

2005年に基本的な枠組みがFrank Bretzら[1]によって提案されて以来、拡張され続けてします。サンプルサイズ設計[2]、非常によくできているRのDoseFindingパッケージ(以前はMCPModパッケージという名前)の開発[3]、 $Y$ が二値など正規分布以外の場合への適用[4]などの発展があります。今後も使用が広がっていくと思われます。

Rの`DoseFinding`パッケージの使い方

医療統計の分野で開発されたため、 $X$ がdose（用量）、 $Y$ がresp（レスポンス）やeff（効果）という名前になっていますが、そこはあまり気にせずに先に進みます。

モデルの準備

library(DoseFinding)

doses <- seq(from = 0, to = 8, by = 2)
models <- Mods(doses = doses, maxEff = 1.65,
               linear = NULL, emax = 0.79, sigEmax = rbind(c(4, 5), c(3, 4)),
               exponential = 1, quadratic = - 1/12)

Mods関数でモデルたちを準備します。モデルとは用量 $X$ と効果 $Y$ の平均（ここでは $\mu$ と呼ぶことにします）を表す曲線のことを指します。引数dosesは実験で使用するdosesです。引数maxEffはそのdosesの範囲での $\mu$ の最大値です。

以降の引数はモデルの定義です。想定するモデルの形状パラメータの値まで与える必要があります。それが各引数で与えている数値になります。事前に用意するのはかなりハードルが高そうに思えますが、検定が厳密であるため仕方ありません。形状パラメータの推定は検定後に改めてModelingステップで行われるので、そこまで頑張らないで雰囲気で決めます。モデルの選択肢と数値の意味はmanualを参照してください。なおモデルは最低用量における $\mu$ からの差分を表します。例えば、linearモデルは（最低用量における） $\mu$ が0で、（最高用量における） $\mu$ が1.65であることから、切片と傾きが決まるので何も数値を与える必要がなくNULLを指定しています。上記のsigEmaxのようにrbindで複数の引数を渡すと、式は同じだけど形状パラメータの値が異なるモデルが2つ作られます。

準備したモデルの候補について、 $\mu$ の値を取得するにはgetResp関数を使います。

resps <- getResp(models, doses = doses)

準備したモデルを可視化するには、plot関数を使います。

plot(models)

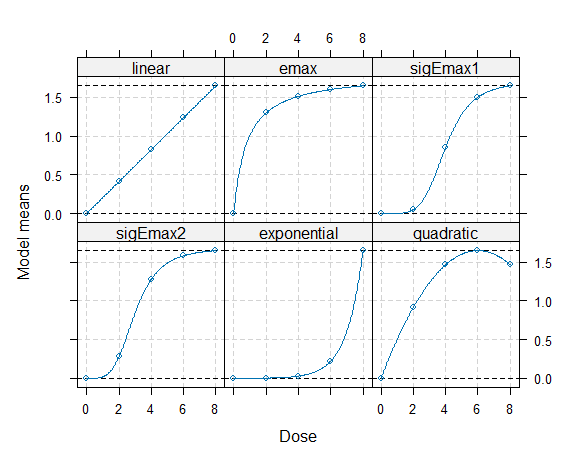
データを得たあとの適用

ここでは例として0,2,4,6,8の5つのdosesのそれぞれについて、30人ずつ割り付けてデータを取得したとします。また、真のモデルを仮にemaxとし、真の観測誤差の分散を4.5としています。

set.seed(123)

resps_true <- resps[, 'emax']
sim_doses_idx <- rep(1:5, each = 30)
sim_doses <- doses[sim_doses_idx]
sim_resps <- rnorm(n = length(sim_doses), mean = resps_true[sim_doses_idx], sd = sqrt(4.5))

resmm <- MCPMod(sim_doses, sim_resps, models = models, 
                Delta = 1.3, alpha = 0.025, selModel = 'AIC')

MCPMod関数の一行で多重検定とモデル選択とおすすめの用量の計算を行っています。引数Deltaはおすすめの用量の計算で使われています。 $\mu$ がDeltaとなるようなdoseの値がおすすめの用量になります。引数alphaは片側有意水準です。帰無仮説はどの用量でも値が変わらない平らな直線に相当します。引数selModelはモデル選択を行うときの基準です。デフォルトではAICが使われます^[1]。有意だったモデルたちすべてについてデータへあてはめを行い、その中で最もAICが小さいモデルが選ばれて後述するselModになります。

結果の取り出しなど

選択されたモデルを取り出すには以下のようにします。どれも有意でない場合はNULLになります。

selmod <- resmm$selMod

各曲線のp値は以下で取り出します。

pvals <- attr(resmm$MCTtest$tStat, 'pVal')

おすすめの用量の値は以下で取り出します（medはMinimum Effective Doseの略です）。

med <- unname(resmm$doseEst[selmod])

選択されたモデルの $\mu$ の推定値は以下で求めます。

resps_est <- predict(resmm$mods[[selmod]], predType = 'ls-means', doseSeq = doses)

漸近論ベースの最適な割り付け比率

DoseFindingパッケージでは、D-optimal法[5]を使って推定する形状パラメータの分散が最小になるという意味で最適な割り付け比率を求めることができます。具体的には、 $N\rightarrow \infty$ のときに次の式を最小化する割り付け比率を求めます。

-\sum_{m}\frac{p_m}{k_m}\operatorname{log}\left(\operatorname{det}M_m\right)

ここで $m$ はモデルのインデックス、 $p_m$ はモデル $m$ の事前の確率、 $k_m$ はモデル $m$ の形状パラメータの数、 $M_m$ はモデル $m$ のもとでのフィッシャー情報行列になります。例えば、上で定義した $6$ つのモデルの事前の確率が $1/6$ ずつだった場合に最適な割り付け比率を求めるRコードは次になります（Rsolnpパッケージのインストールが必要になるかもしれません）。

optDesign(models, probs = rep(1/6, 6))

参考文献

[1] Bretz, F., Pinheiro, J. C., & Branson, M. (2005). Combining multiple comparisons and modeling techniques in dose-response studies. Biometrics, 61(3), 738-748.
[2] Pinheiro, J., Bornkamp, B., & Bretz, F. (2006). Design and analysis of dose-finding studies combining multiple comparisons and modeling procedures. Journal of biopharmaceutical statistics, 16(5), 639-656.
[3] Bornkamp, B., Pinheiro, J., & Bretz, F. (2009). MCPMod: An R package for the design and analysis of dose-finding studies. Journal of Statistical Software, 29, 1-23.
[4] Pinheiro, J., Bornkamp, B., Glimm, E., & Bretz, F. (2014). Model‐based dose finding under model uncertainty using general parametric models. Statistics in medicine, 33(10), 1646-1661.
[5] Dragalin, V., Hsuan, F., & Padmanabhan, S. K. (2007). Adaptive designs for dose-finding studies based on sigmoid e max model. Journal of Biopharmaceutical Statistics, 17(6), 1051-1070.

脚注

AICだとパラメータ数の少ないlinearやemaxが選ばれる確率が増える傾向があります。あてはまり重視ならば、検定を行ったときのT統計量であるmaxTを使うと良いでしょう。 ↩︎