『Pythonではじめる数理最適化』の7章「商品推薦のための興味のスコアリング」をStanで解く

この記事は確率的プログラミング言語 Advent Calendar 2023の12/8の記事です。

概要

『Pythonではじめる数理最適化』はいい本ですよね。親しみやすい実例、分かりやすい数式、きれいなPythonコードと三拍子そろっています (今年のアドカレで改訂版が近いうちに出ることを知りました)。
https://amzn.to/40Zuer1
7章「商品推薦のための興味のスコアリング」では、「何日前に直近の閲覧があったか」と「閲覧回数」の二つの軸で興味のスコアを考えます。興味のスコアが単調減少であるという制約のもと、再閲覧の割合と推定値の二乗誤差を最小化するという凸二次計画問題として解いています。この記事ではStanで解くとこんな感じですというのを示します。メリットとしてベイズ信頼区間も推定されます。

データ

公式のリポジトリの7章のipynbファイルを途中まで実行して得られるデータフレームrf_dfを使用します。他の人の扱いやすいさのため、csvで出力して保存しておきました。以下になります。

各列の説明は以下の通りです。

• rcen:何日前に直近の閲覧があったか
• freq:それまでに閲覧した回数
• N:rcenとfreqのペアに対する総件数
• pv:rcenとfreqのペアに対する再閲覧の件数
• prob:再閲覧の割合 (pv/N)

目的

rcen(以降$r$)とfreq(以降$f$)で定まる関数として再閲覧確率$q(r,f)$を推定することです。ただし、同じ$r$の値ならば$f$が大きいほど$q(r,f)$の値は高く、同じ$f$の値ならば$r$が大きいほど$q(r,f)$の値は小さくなるという制約を入れたいです。

以下では分かりやすさのため、$q(r,f)$は$r$,$f$の両方について単調減少としたいので、データ内の$f$の最大値+1である8から引いて、$f$を$8-f$に置き換えて考えることにします。

確率的プログラミング言語におけるモデル

確率的プログラミング言語では、割合の値をそのまま使わない方が良いケースがほとんどです。代わりに、（分母の）総件数と（分子の）再閲覧の件数を二項分布と組み合わせて使います。そうすることで分母・分子の値が小さいときの不確実性をモデルに取り込むことができるからです。

2次元の単調減少(厳密には非増加)の関数を表現するのは少し工夫が必要です。構成方法の一例を挙げます。$q(1,1)$から順番に構成していくことを考えます。はじめに$r=1$について

$$q(1,f) = q(1,f-1) - \delta(1,f) \qquad f=2,\ldots,F$$

（ただし$\delta(1,f) \ge 0$）と表現します。同様に$f=1$について

$$q(r,1) = q(r-1,1) - \delta(r,1) \qquad r=2,\ldots,R$$

（ただし$\delta(r,1) \ge 0$）と表現します。次に、$r \ge 2$と$f \ge 2$のケースですが、以下のように構成すれば単調減少を満たします（ただし$\delta(r,f) \ge 0$）。

$$q(r,f) = \operatorname{min}(q(r-1,f), q(r,f-1)) - \delta(r,f)$$

コード

$q(r,f)$は確率なので$[0, 1]$の値を持ちます。そこで$(-\infty, \infty)$の値域をもつlogitの空間で単調減少の$x(r,f)$を構成しておいて、最後にinv_logit関数で確率にします。そして$\delta(r,f)$をdx[r,f]と書きます。ここではdx[r,f]については特に制限つけないで推定します。

• 2行目：縦持ちのデータのままStanに渡します。Iはその縦持ちのデータ数（行数）になります。
• 18行目：x[1,1]は制約なしの別パラメータとして宣言してもよいのですが、コードをすっきりするために、dx[1,1]を使っています。5 - dx[1,1]とすることでq[1,1]の最大値をinv_logit(5) = 0.9933に設定していることに相当します。

上記のモデルを実行するPythonコードは以下の通りです。10秒ほどで推定結果が得られました。

推定結果

公式のリポジトリから可視化の部分のコードを転用しまして、qのMCMCサンプルの中央値をプロットすると以下になりました。数理最適化の結果と微妙に異なる部分がありますかね。

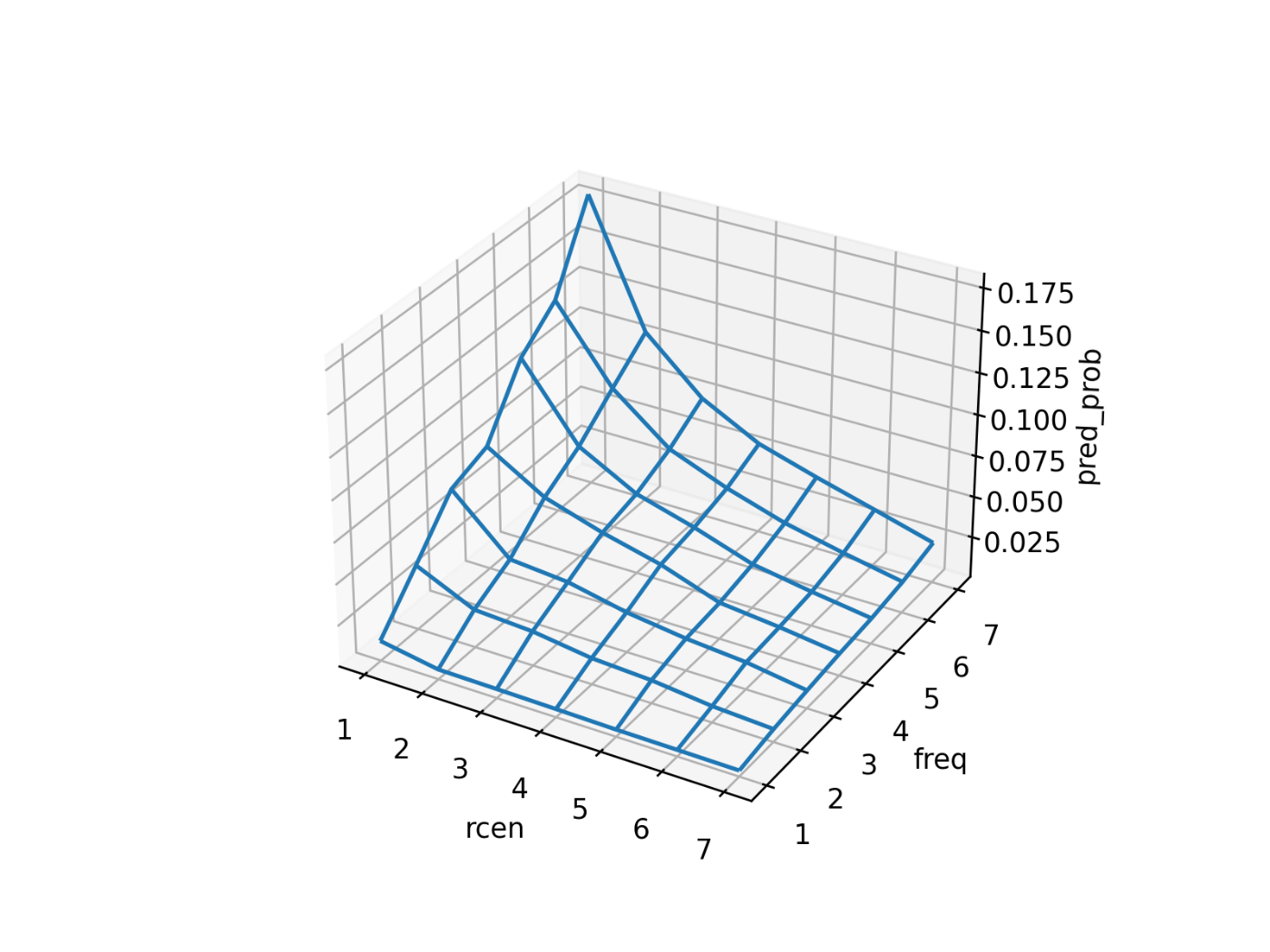
MCMCサンプルが得られているので、ベイズ信頼区間やベイズ予測区間も算出できます。例えば、$f=5$に沿ったqの断面図をベイズ信頼区間つきでプロットすると以下になります(青帯は95%ベイズ信頼区間と50%ベイズ信頼区間、青折れ線は中央値、黒点はデータのprob)。

Enjoy!