APR vs. APY in DeFi：初学者のための単利と複利の再整理

導入

APRを使用して収益を概算したり、

APYをAPRに換算して比較したり、

DefiプロジェクトのAPR・ APYの表示の実装を分析したりする機会があったため、
 
 
Defiの世界で頻繁に使用されるAPR、および、APYについて整理してまとめました。

今回は、「Defi」におけるAPR・APYについてまとめていきます。
 
 
自身の備忘録的意味合いが強いため、かなり冗長となっております。ご了承ください。
 
 

まとめ

下記を全て読んでる時間がない方へ

- 連続単利？-

連続的に進行する時間$t$で都度利子が発生する前提の単利計算

-単利合計-

$$P \times r \times \frac{t}{T}$$

• $P$：元本（初期投資額）
• $r$：金利
• $t$：経過時間
• $T$：基準時間

-元利合計-

$$P(1+ r \frac{t}{T})$$

• $P$：元本（初期投資額）
• $r$：金利
• $t$：経過時間
• $T$：基準時間

-連続複利-

連続的に進行する時間で都度利子が発生する前提での単位期間数$t$経過した際の複利計算

-複利合計-

$$I_t =P ( e ^{rT} -1)$$

• $P$：元本（初期投資額）
• $r$：金利
• $T$：経過期間数

-複利利回り-

$$R_t =e ^{rt} -1$$

• $r$：金利
• $t$：単位期間の経過期間数

-元利合計-

$$V_t =P \times e ^{rt}$$

• $P$：元本（初期投資額）
• $r$：金利
• $t$：単位期間の経過期間数

-APR-

$$\text{APR} = \left( \left( \frac{F + I}{P} \right) \times \frac{365}{n} \right) \times 100$$

• $I$： ローン期間全体で支払われた総利子
• $P$ ： 元金（借入金額）
• $F$： 手数料
• $n$ ： ローン期間の日数

-DefiにおけるAPR-

１年単位での「単利」の「利率」

年間金利を$r$とすると、

$$\text{APR}=100\times r$$

-APY-

$$\text{APY}=100\times\left\{ (1 + \frac{r}{m})^m - 1 \right\}$$

• $m$：単位期間あたりの複利計算回数
• $r$：金利

-DefiにおけるAPY-

１年単位での「複利」の「利率」

年間金利を$r$とすると、

$$\text{APY}=100\times\left( e ^{r} -1 \right)$$

- DefiにおけるAPYのAPR換算式-

年間金利を$r$とすると、任意のDefiプロジェクトにおけるAPYのAPRへの換算式

$$\text{APR}=100\times\ln\left(\frac{\text{APY}}{100} + 1\right)$$

 
 

概観

まずは用語を整理した上で、単利、複利の理解を深め、

そののちに、APR・APYの詳細を整理していきます。

 
 

用語の整理

本記事においては以下で統一させていただきます。

元本：
最初に貸し借りしたトークンの「量」。

利子（利息）：
貸し借りの際、元本とは別に発生する対価のトークンの「量」。

金利：
「元本」に対する「利子」の「比」。$\text{金利}=\frac{\text{利子}}{\text{元本}}$

単利計算：
後述。

複利計算：
後述。

単利：
「元本」に対して、「単利計算」で計算した「利子」。

複利：
「元本」に対して、「複利計算」で計算した「利子」。

利率：
「元本」に対する「利子」の「百分率」。$\text{利率}=100\times\frac{\text{利子}}{\text{元本}}$

元利（元利合計）：
元金と利子。また、その合計「量」。$\text{元利}=\text{元本}+\text{利子}$

APR：
年単位での「単利」の「利率」。

APY：
年単位での「複利」の「利率」。
 
 

本題

APR（Annual percentage rate）とAPY（Annual percentage yield）

単利（計算）と複利（計算）

「単利計算」「複利計算」の計算方法を数式を用いて丁寧に確認し、

その後、「APR」「APY」を確認していきます。
 
 
まず、

「単利計算」「複利計算」とは「利子」の計算方法であり、

その結果得られる「利子」を「単利」「複利」といいます。
 
 
以下のグラフをご覧ください。

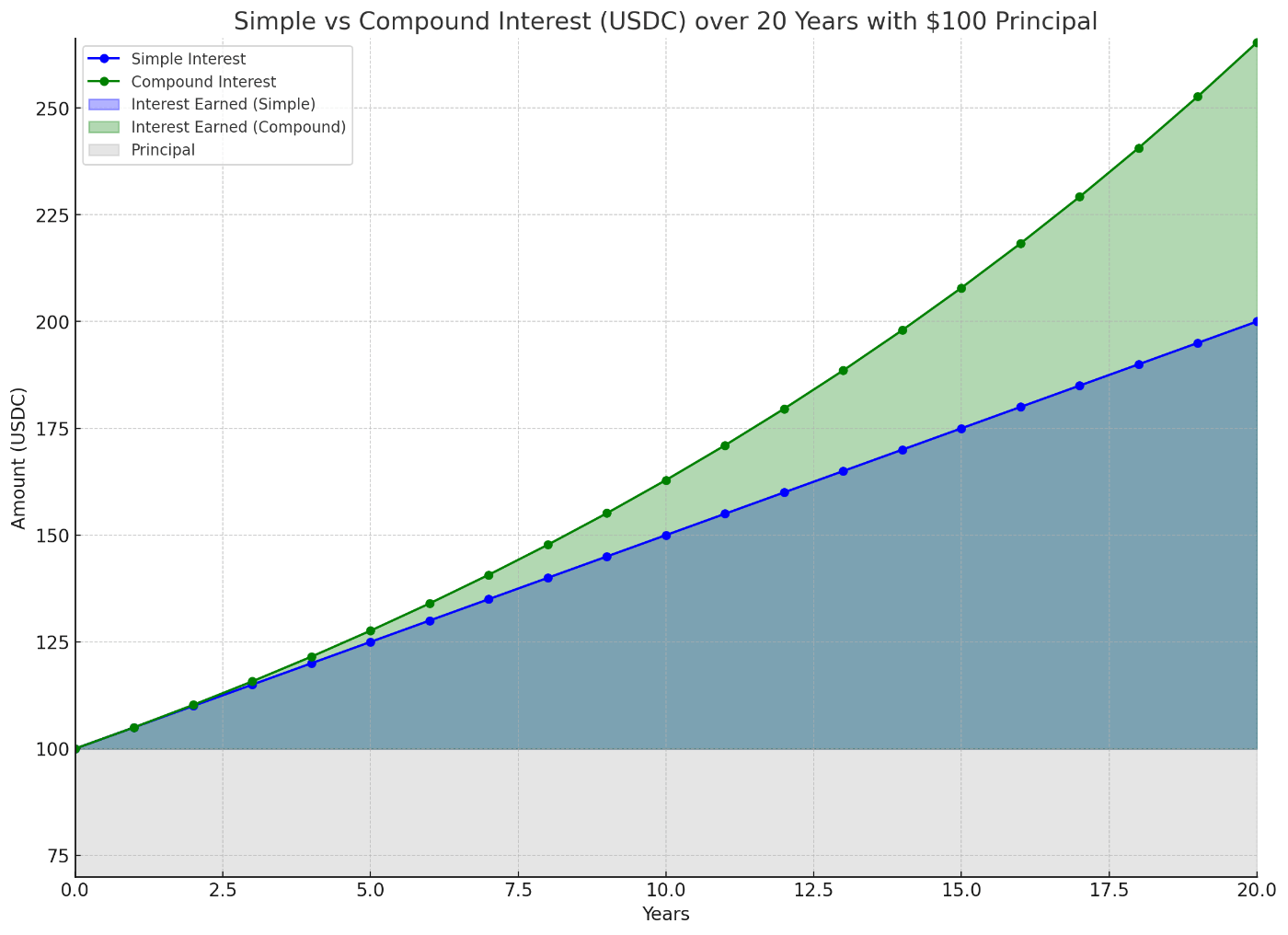
これは、金利が一定であると仮定した場合の、単利計算、複利計算による元利合計のグラフです。

 
 
灰色が、元本。

青色（重なっているため正確には紫色）が、単利で、

緑色が、複利です。

 
 
ここでなんとなく、

単利が線形的な増加、複利が指数関数的な増加をしていると感じていただければ幸いです。
 
 

単利計算

大まかにイメージできたところで個々の計算方法を見ていきます。

 
 
単利計算の場合、シンプルにいうと、利子を再活用しない計算方法です。
 
 

例えば、得られた利子を元本として再投資しません。

したがって、期間ごとに得られた利子には、金利がつきません。
 
 

金利が一定であると仮定すると、元本は一定ですから、

元利合計の増加は線形的になります。

 
 
将来の元利合計の計算式は以下となります。

$$V_t = P + P \times r \times t$$

$$V_t = P(1+ r t)$$

• $V_t$：$ t $期間における元利合計
• $P$：元本（初期投資額）
• $r$：金利
• $t$：期間数

また、グラフは以下のようになります。

 
 

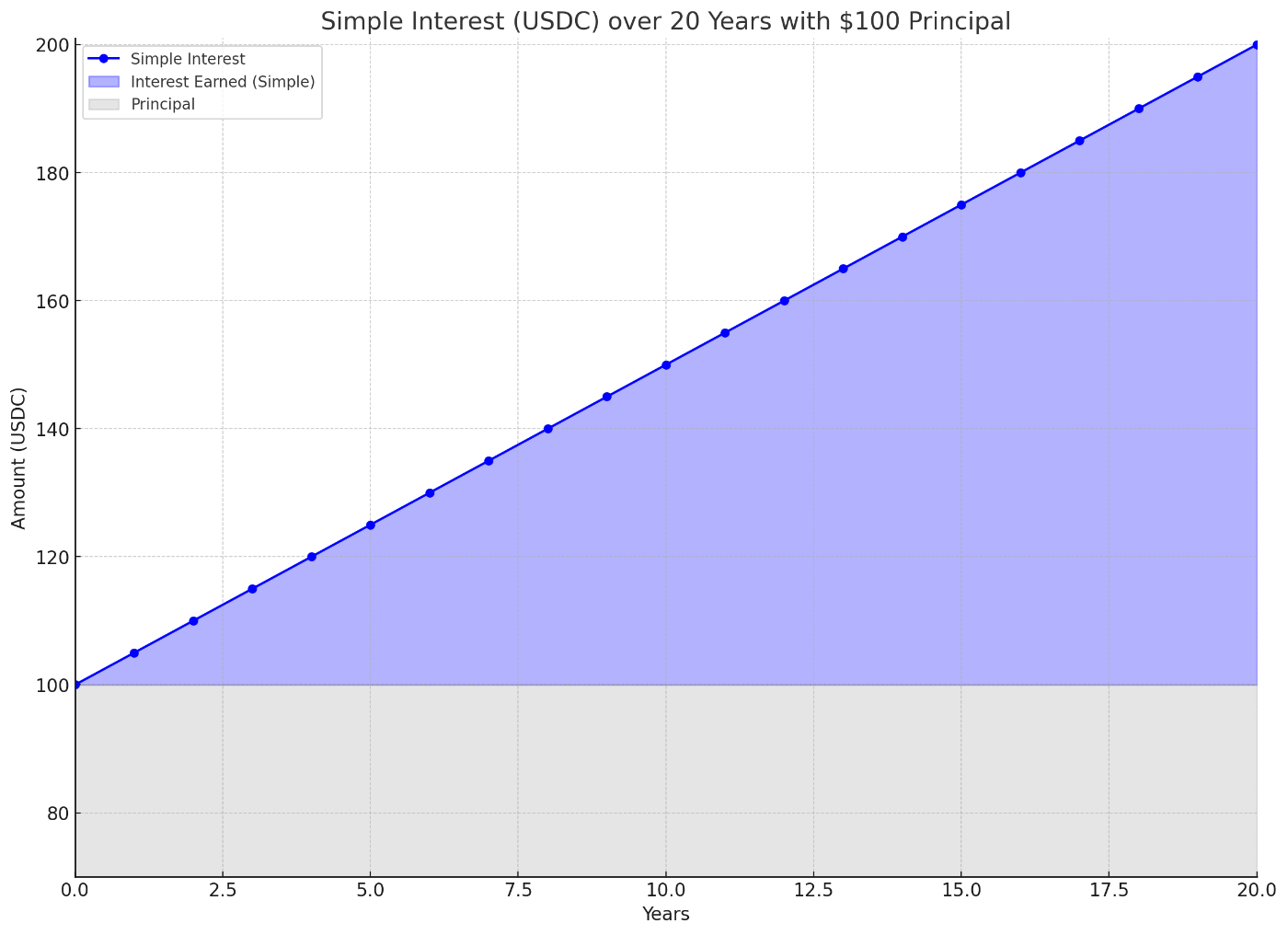
どうしてこのような式になるのか、順を追って見ていきます。

まずは、利子に着目します。つまり、単利に着目します。
 
 

単利の算出

元本$P$に金利$r$を掛けることで１期間の利子（単利）が求められ、

これを期間$t$に渡って計算し、その結果得られた利子を元本に加えることで、

元利合計を求めることができます。
 
 

１期間の利子（単利）

１期間におけるの利子$I_1$は次のように計算されます。

$$I_1 = P \times r$$

$$I_1= P \times r \times 1$$

 
 
２期間の利子（単利）

２期間におけるの利子$I_2$は次のように計算されます。

$$I_2= P \times r + P \times r$$

$$I_2= P \times r \times 2$$

 
 

この流れから、$t$期間後の利子は自ずと以下になります。
 
 

t 期間後の利子（単利）

期間が$t$に渡る場合、利子は毎期間同じ金額が元本に対して発生するため、

総利子、つまり、単利の合計$ I_t $は次のように計算されます。

$$I_t = P \times r \times t$$

• $I_t$：$ t $期間における単利合計
• $P$：元本（初期投資額）
• $r$：金利
• $t$：期間数
   
   

元利合計：元本と単利の合計

では、あとは簡単です。
 
 

元本と単利の合計額、

つまり、元利合計$V_t$は、元本に先ほど算出した利子$I_t$を加えたものになります。

$$V_t = P + I_t$$

 
 

では、先ほど導出した$I_t = P \times r \times t$を代入すると、

$$V_t = P + P \times r \times t$$

$$V_t = P(1+ r t)$$

単利計算における元利合計を表す式となります。
 
 

連続単利？：単利計算における期間数$t$の拡張

単利合計、単利計算における元利合計の式を以下でした。

$$I_t = P \times r \times t$$

$$V_t = P(1+ r t)$$

 
 

しかし、まだ不十分であるといえます。

現状、期間数$t$が離散的で（飛び飛びで）連続的に考えられる土台ができていません。
 
 

つまり、年間金利を$r$とした場合、

$I_t = P \times r \times t$$V_t = P(1+ r t)$のままでは、

１年間を前提にした場合の、１ヶ月経過時点の単利合計、元利合計を算出することができません。
 
 

これの何が問題かというところですが、今、私たちは、「Defi」におけるAPRを知りたいと考えています。
 
 

Defiは、数秒単位で利益が発生します。

そのため、APR、つまり、年間の単利の利率は、１年間で考えつつも、数秒レベルでの話をしているわけです。
 
 

そうすると、繰り返しとなりますが、

$I_t = P \times r \times t$$V_t = P(1+ r t)$のままでは、問題となるわけです。
 
 

したがって、１年、１日のような、１単位となる期間を考えた場合、

その期間より短い期間にも対応可能な数理モデルに修正する必要があります。

 
 
まず、期間の基準を$T$を導入します。

 
 
仮に、この$T$を１年と考え、１年間の単利計算における金利を$r$とすると、

$T$は日ベースであれば$365$と考えられ、また、時間ベースであれば、$365\times24$と置けます。
 
 

そして、その$T$基準でどれほどの時間進行したかを$t$で表すと、

$I_t = P \times r \times t$$V_t = P(1+ r t)$は、以下のように捉え直されます。

$$I_t = P \times r \times \frac{t}{T}$$

$$V_t = P(1+ r \frac{t}{T})$$

 
 

ここで、疑問に持つ人もいるかもしれません。

「何で単純に単利の合計が$T$基準での時間進行$t$の掛け算で計算できるのか？」と。
 
 

これは、以下の図を見れば明確かと思いますが、

飛び飛びの期間、例えば、１年毎の単利計算における金利$r$の変化を考えると、
 
 

１年目は、$r$

２年目も、$r$

３年目も、$r$

と変化しないので、
 
 

０．５年目も、$r$

１．３年目も、$r$

２．７年目も、$r$

と考えられます。
 
 

つまり、金利の変化は０です。

なので、単純に、変化しない金利$r$に時間$t$を掛け算してよく、

基準となる単位が$T$なのであれば、$t/T$をかければ良いという話です。

もっと本格的に書くと、これは微積の話です。
 
 

金利の変化に関しては、

これはまさに、単利計算における金利$r(t)=r$を時間$t$で微分しています。

$$r(t) = r \Rightarrow \frac{d}{dt} r(t) = 0$$

 
 

また、単利計算における金利$r(t)=r$を時間$t$で積分すると、

$$\int r \, dt = rt + C$$

となり、単利が、単に掛け算で表されることが明確にわかります。
 
 

DefiにおけるAPR（Annual percentage rate）

この段階で、ようやくAPRについて考える準備が整いました。
 
 

１年単位での「単利」の「利率」がAPRなわけですから、

まず、連続単利？を再確認します。

$$I_t = P \times r \times \frac{t}{T}$$

 
 

ここで、$T$を年単位とするのであれば、

１年単位での「単利」の「利率」がAPRであるという条件を満たせます。
 
 

単利計算における金利$r$を百分率にすると、「Defiにおける」APRが以下のように導かれます。

$$\text{APR}=100\times r$$

 
 
つまり、

$$I_t = P \times \frac{\text{APR}}{100} \times \frac{t}{T}$$

 
 

「Defiにおける」とわざわざ付け足したのは、

 
 
DefiにおけるAPRと一般に使用されるAPRが別のものに感じたのでこのように表現しております。

 
 
どうやらAPRは、

米国におけるローンの総コストを年ベースで表したもので、以下のように表すようです。

$$\text{APR} = \left( \left( \frac{F + I}{P} \right) \times \frac{365}{n} \right) \times 100$$

• $I$： ローン期間全体で支払われた総利子
• $P$ ： 元金（借入金額）
• $F$： 手数料
• $n$ ： ローン期間の日数
   
   

こちらのAPRについては、本記事ではこれ以上触れないでおきます。

関心がある方は、参考資料のセクションを確認してみてください。
 
 

複利計算

では、対して、複利計算はどうでしょうか。
 
 

複利計算の場合、利子を再活用する計算方法です。
 
 

例えば、得られた利子を元本として再投資します。
 
 

単利計算では、「金利」は「元本」だけを対象にしていましたが、

複利計算においては、「元本＋前タイミング発生した利子の合計」を対象にします。
 
 

したがって、

金利が一定であっても、元本が増加していくため、

増えたものに金利をかける、さらに増えたものに金利をかけるという形で、

元利合計は増えていき、指数関数的に増加します。
 
 

計算式は以下の通りです。

$$V_t = P \times (1 + r)^t$$

• $V_t$：将来の元利合計
• $P$：元本（初期投資額）
• $r$：年利率
• $t$：経過年数
   
   

また、グラフは以下のようになります。

 
 

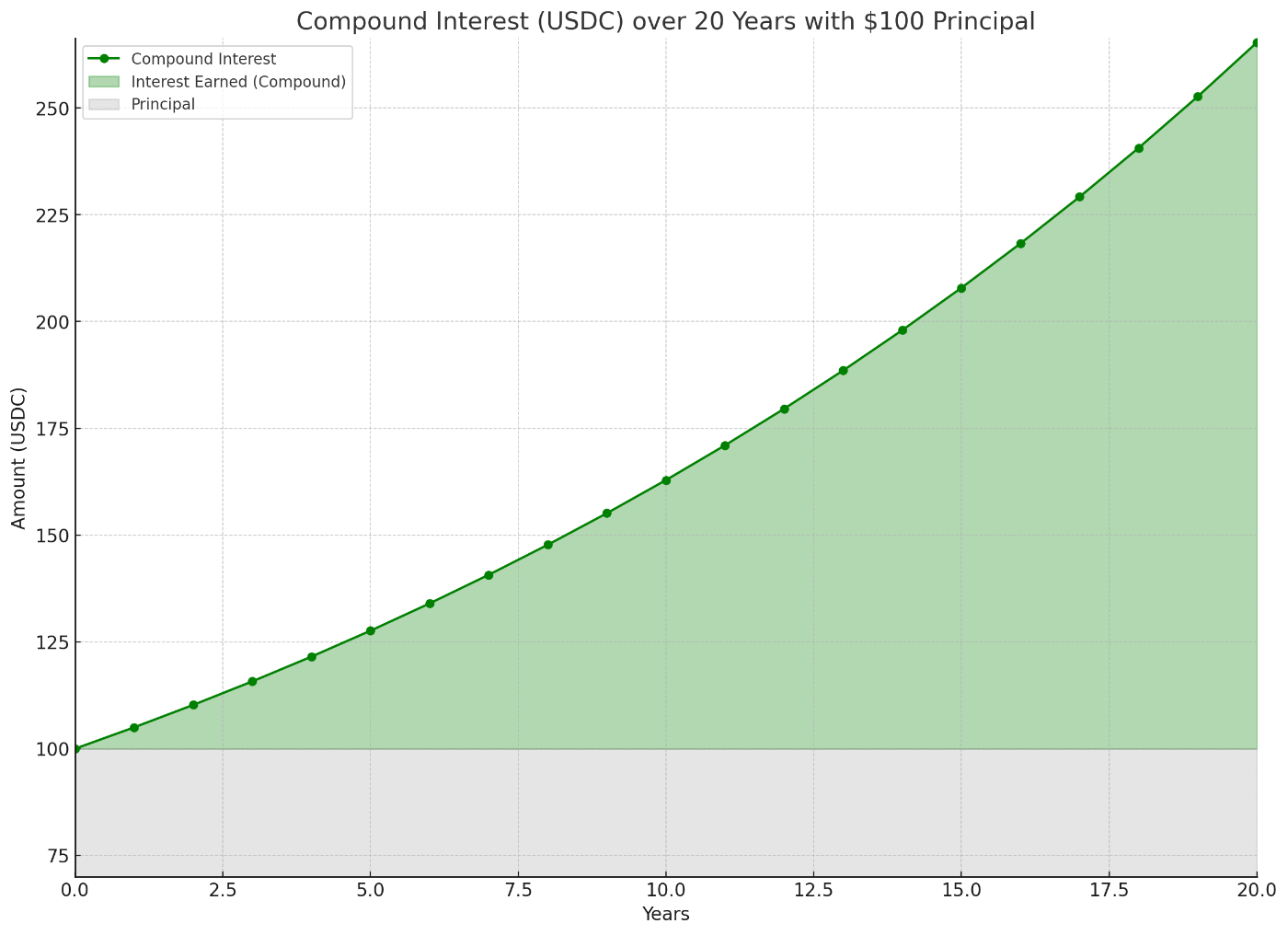
では、どのようにこの式を導くのか、

複利は、単利とは違って元本が変化していきますので、

元本に注目して、順を追って見ていきましょう。
 
 

元利合計でもある元本の算出

初期値（０期間）

元本$P$のみ所持しています。
 
 

１期間後の元本

１期間後の元本（であり元利）$V_1$ は、

元本$P$に金利$r$の利子を加えたものになります。

$$V_1 = P+P \times r$$

$$V_1 = P \times (1 + r)$$

 
 
２期間後の元本

２期間後の元本（であり元利）$V_2$ は、

1期間後の元本$V_1$ に金利$r$の利子を加えたものになります。

$$V_2 = V_1 +V_1\times r$$

$$V_2 = V_1 \times (1 + r)$$

$$V_2= P \times (1 + r) \times (1 + r)$$

$$V_2= P \times (1 + r)^2$$

 
 

３期間後の元本

同様に、3期間後の元本（であり元利）$V_3$は、

$$V_3 = V_2 +V_2\times r$$

$$V_3 = V_2 \times (1 + r)$$

$$V_3= P \times (1 + r)^2 \times (1 + r)$$

$$V_3= P \times (1 + r)^3$$

 
 

t 期間後の元本

このように、

複利計算では、元本に金利$r$を掛けたものが繰り返し元本に加えられていくので、

$t$期間後の元本$V_t$は次のように表されます。

$$V_t = P \times (1 + r)^t$$

• $V_t$：$ t $期間における元本、元利合計
• $P$：初期元本（初期投資額）
• $r$：金利
• $t$：期間数（複利の計算回数）

 
 

では、複利計算による利子にも着目して見てみましょう。つまり、複利に着目します。

 
 

複利の算出

$t$期間後の複利計算による利子の総額 $ I_t$ は、次のように計算されます。

単に、初期元本を元利合計から引き算して導きます。

$$I_t = V_t - P$$

$$I_t = P \times (1 + r)^t - P$$

$$I_t = P \left\{ (1 + r)^t - 1 \right\}$$

• $V_t$：$ t $期間における元本、元利合計
• $P$：初期元本（初期投資額）
• $r$：金利
• $t$：期間数（複利の計算回数）
   
   

複利計算における期間数$t$の拡張

ここで、

複利における、元利合計に関する式と複利の算出に関する式を再度確認します。

$$V_t = P \times (1 + r)^t$$

$$I_t = P \left\{ (1 + r)^t - 1 \right\}$$

この式は、期間数$t$の内、１期間に１回だけ複利計算されるという制限されたモデルです。
 
 

現状、

DefiにおいてのAPR・APYを考えているわけですが、これらは１年間の金利をもとに考えています。
 
 

しかし、Defiの世界で１年間に１回だけ複利計算される実装はほぼありません。

秒レベルの単位で複利計算されています。
 
 

したがって、期間数$t$の１期間に、

任意の回数複利計算が行われた場合の計算に、対応できるよう拡張します。
 
 

ここでは、その１期間内に複利計算が行われる回数を $m $とし、

まず、元本を $P $として、初回複利計算後の元本をみてみましょう。
 
 

ここで一旦復讐しておきます。

初回の複利計算は以下のようになりました。

$$V_1 = P+P \times r$$

$$V_1 = P \times (1 + r)$$

 
 

また、2回目の複利計算は以下で表されました。

$$V_2 = V_1 +V_1\times r$$

$$V_2 = V_1 \times (1 + r)$$

$$V_2= P \times (1 + r) \times (1 + r)$$

$$V_2= P \times (1 + r)^2$$

 
 

その結果

$$V_t = P \times (1 + r)^t$$

が導かれました。
 
 

この全期間$t$の「１期間」内に複利計算が行われる回数を $m $として、拡張を進めていきます。
 
 

イメージを掴むため、以下の画像を見てください。

「一定期間毎」に、「一定の金利」を、

元本にかけて、再利用するというのが複利計算の基本的な考え方です。
 
 

この考えをもとにして、

「１期間」を$m$で等分した場合、対応する「一定の金利」も$m$等分されると考えます。
 
 

したがって、期間$t$後の、

つまり、最終的なゴールの元本（元利合計）が、$V_t = P \times (1 + r)^t$であったことから、
 
 

１期間を$m$で等分した場合の、

最終的なゴールの元本（元利合計）は、$V_t = P \times (1 + \frac{r}{m})^m$となります。
 
 

^$m$となるのは、全期間$t$の「１期間」内に複利計算が行われる回数を $m $と考えているからです。
 
 

以上から「１期間」内に複利計算が$m$回行われる元利合計、複利合計は以下となります。

$$V = P \times (1 + \frac{r}{m})^m$$

$$I = P \left\{ (1 + \frac{r}{m})^m - 1 \right\}$$

 
 

最終的にはこのようなイメージとなります。

 
 

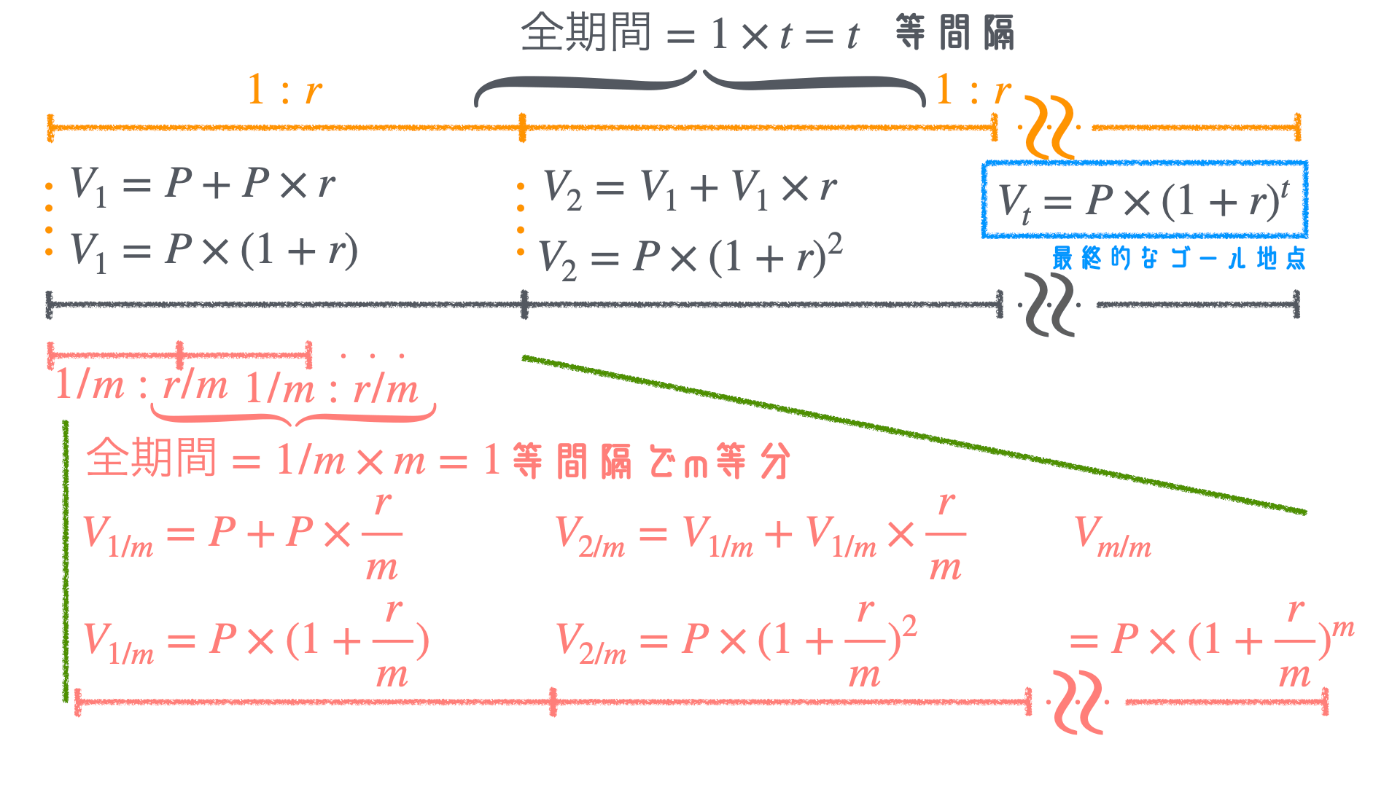
複利計算における基準となる期間$T$の拡張

これらをさらに一般化します。

$$V = P \times (1 + \frac{r}{m})^m$$

$$I = P \left\{ (1 + \frac{r}{m})^m - 1 \right\}$$

基準となる期間（年、日etc.）を$T$として、

その$T$期間において、$n$回複利計算が行われると仮定すると、
 
 

$T$期間内１回目の複利計算による元利合計

$$V_{1/T} = P+P \times \frac{r}{n}$$

$$V_{1/T} = P \times (1 + \frac{r}{n})$$

 
 

$T$期間内２回目の複利計算による元利合計

$$V_{2/T} = V_1 +V_1\times \frac{r}{n}$$

$$V_{2/T} = V_1 \times (1 + \frac{r}{n})$$

$$V_{2/T} = P \times (1 + \frac{r}{n}) \times (1 + \frac{r}{n})$$

$$V_{2/T} = P \times (1 + \frac{r}{n})^2$$

 
 

$T$期間内n回目の複利計算による元利合計

$$V_{n/T} = P \times (1 + \frac{r}{n})^n$$

 
 

$2T$におけるの複利計算による元利合計

$$V_{2 \times \frac {n}{T}} = P \times (1 + \frac{r}{n})^{2 \times n}$$

 
 

$t \times T$におけるの複利計算による元利合計

$$V_{t \times \frac {n}{T}} = P \times (1 + \frac{r}{n})^{t \times n}$$

 
 

以上で基準となる期間を跨ぐ場合にも、本モデルが取り扱えるようになりました。
 
 

連続複利

では、

$$V_{t \times \frac {n}{T}} = P \times (1 + \frac{r}{n})^{t \times n}$$

における$n$を無限に大きくするとどうなるでしょう。

今までは、拡張してもまだ離散的、つまり、飛び飛びの値の世界でした。

しかし、図のように、無限に$n$を大きくすることで、

飛び飛びの分割点が連続になっているかのような世界に持ち込めます。
 
 

このような連続的な複利計算を「連続複利」といいます。

 
 
では、連続複利をベースとした、元利合計の拡張モデルを導きましょう。

 
 
まず、

$$V_{t \times \frac {n}{T}} = P \times (1 + \frac{r}{n})^{t \times n}$$

における、$n$を無限に大きくすると、以下のような数式のイメージになります。

$$V_{t \times \frac {\infty }{T}} = P \times (1 + \frac{r}{\infty })^{t \times \infty }$$

正確には、以下のように記述します。

$$\lim_{n \to \infty} V_{t \times \frac {n}{T}} = \lim_{n \to \infty} \left[P \times (1 + \frac{r}{n})^{t \times n} \right]$$

$$\lim_{n \to \infty} V_{t \times \frac {n}{T}} =P \times \lim_{n \to \infty} \left[(1 + \frac{r}{n})^{t \times n} \right]$$

 
 

ここで、指数法則を用いて式変形します。

$(a^m)^n=a^{m \cdot n}$より

$$\lim_{n \to \infty} V_{t \times \frac {n}{T}} =P \times \lim_{n \to \infty} \left[ \left\{ \left(1 + \frac{r}{n}\right)^{\frac{n}{r}} \right\}^{rt} \right]$$

ここで、

$$l=\frac{n}{r}$$

とおくと

$$\frac{r}{n}=\frac{1}{l}$$

また、

$n \to \infty$のとき$ l=\frac{n}{r}$から$l \to \infty$であることに加えて、

$$\lim_{l \to \infty} (1 + \frac{1}{l})^{l} =e$$

であることから

$$\lim_{n \to \infty} V_{t \times \frac {n}{T}} =P \times \lim_{n \to \infty} \left[ \left\{ \left(1 + \frac{r}{n}\right)^{\frac{n}{r}} \right\}^{rt} \right]$$

は、

$$\lim_{l \to \infty} V_{t \times \frac {n}{T}} =P \times \lim_{n \to \infty} \left[ \left\{ (1 + \frac{1}{l})^{l} \right\}^{rt} \right]$$

$$\lim_{l \to \infty} V_{t \times \frac {n}{T}} =P \times \left\{ \lim_{n \to \infty} (1 + \frac{1}{l})^{l} \right\}^{rt}$$

$$\lim_{l \to \infty} V_{t \times \frac {n}{T}} =P \times \left\{ e \right\}^{rt}$$

$$\lim_{l \to \infty} V_{t \times \frac {n}{T}} =P \times e ^{rt}$$

となります。
 
 

したがって、無限に分割した場合の元利合計は、以下となります。

$$V_t =P \times e ^{rt}$$

 
 
ここでの$t$は、先ほど導いた

$t \times T$におけるの複利計算による元利合計

$$V_{t \times \frac {n}{T}} = P \times (1 + \frac{r}{n})^{t \times n}$$

における$t$であり、$r$は金利です。
 
 

また、連続複利による複利$I_t$は、

$$I_t =P \times e ^{rt} -P$$

$$I_t =P ( e ^{rt} -1)$$

と導けます。
 
 

APY（Annual percentage yield）

大変長くなりましたが、ここでようやくAPYの言及ができます。
 
 

これまでの話から、１年間の複利計算の回数を$m$回とすると、

元利合計、複利合計は以下のように表せました。

$$V = P \times (1 + \frac{r}{m})^m$$

$$I = P \left\{ (1 + \frac{r}{m})^m - 1 \right\}$$

 
 

特に、$I = P \left\{ (1 + \frac{r}{m})^m - 1 \right\}$における、

$\left\{ (1 + \frac{r}{m})^m - 1 \right\}$が複利計算における金利なわけですから、
 
 

年単位での「複利」の「利率」であるAPYは以下のようになります。

$$\text{APY}=100\times\left\{ (1 + \frac{r}{m})^m - 1 \right\}$$

DefiにおけるAPY（Annual percentage yield）

さて、ここで、１年間の複利計算の回数を$m$回に着目します。

Defiにおいて、この$m$は莫大な数になりうることを確認しましょう。
 
 

例えば、ブロック単位で複利計算を行うDefiがあったとします。

Ethereumのブロックタイムは、およそ15秒と仮定すると
（参考：Ethereum Average Block Time Chart）

$$m=\frac{365 \times 60 \times 60}{15} = 31,536,015$$

約3000万回複利計算が行われます。
 
 

したがって、連続複利（連続的な複利計算）であると仮定し、

$$I_t =P ( e ^{rt} -1)$$

を前提に考えると、
 
 

DefiにおけるAPYは、１年間という前提から$t=1$となり、

$$\text{APY}=100\times\left( e ^{r} -1 \right)$$

 
 

APYのAPR換算式

再度APRとAPYを確認してみます。

$$\text{APR}=100\times r$$

$$\text{APY}=100\times\left( e ^{r} -1 \right)$$

 
 

ここで、APYを$r$について解くと

$$\text{APY}=100\times\left( e ^{r} -1 \right)$$

$$\frac{\text{APY}}{100} = e^r - 1$$

$$\frac{\text{APY}}{100} + 1 = e^r$$

$$\log_e\left(\frac{\text{APY}}{100} + 1\right) = \log_e\left(e^r\right)$$

$$\ln\left(\frac{\text{APY}}{100} + 1\right) = \ln\left(e^r\right)$$

$$r = \ln\left(\frac{\text{APY}}{100} + 1\right)$$

 
 

さらに、

$$r = \ln\left(\frac{\text{APY}}{100} + 1\right)$$

$$100\times r = 100\times\ln\left(\frac{\text{APY}}{100} + 1\right)$$

$$\text{APR}=100\times\ln\left(\frac{\text{APY}}{100} + 1\right)$$

 
 

以上のように、

DefiにおけるAPYを、連続複利計算と仮定した場合、

APYをAPRとして捉え直した場合の値を導ける。

$$\text{APR}=100\times\ln\left(\frac{\text{APY}}{100} + 1\right)$$

 
 

では、この式を利用して、実際のAPYをAPRに換算してみましょう。

あるレンディングプロトコルで、$\text{APY}=89.1％$だったものを計算すると、

$$\text{APR}=100\times\ln\left(\frac{\text{89.1}}{100} + 1\right)$$

$$\text{APR} \approx 63.7$$

 
 

このように計算できます。

手元のGoogleSpreadSheetで

= 100  * LN(("APYの書かれたセルを指定" / 100) + 1)

と入力すると、計算できますので試してみてください。
 
 

補足

補足１：名目金利（Nominal Interest）と実効金利（Effective Interest）

金利には、名目金利と実効金利の 2 つの形式があります。
 
 

文脈によって意味が違ってきますが、

名目金利は、コストやリターンなど加味しない目安となるような金利のことをいい、

実行金利は、コストやリターンなど細かい要素を加味したより正確に実態を表した金利のことをいいます。
 
 

では、より詳しく、複利の文脈で見てみましょう。
 
 

例えば、「年間の利率が 10% である」という記述は、１年間ごとに10% で複利計算されることを意味します。

この場合、名目年利は 10% で実効年利も 10% です。
 
 

ただし、複利計算が年に 1 回よりも多く行われる場合、実効金利は 10% より大きくなります。

これは、元本に複利分が追加される回数が多くなるためで、

複利計算の頻度が高ければ高いほど、実効金利は高くなります。
 
 

複利計算の文脈において、実効金利 $i$ は、次の式で表されます。

$$i = \left( 1 + \frac{r}{m} \right)^m - 1$$

• $r$： 名目金利（任意の期間における金利）
• $m$：複利計算の回数（その期間内で何回複利計算が行われるか）
• $i$：実効金利（その期間における実質的な利率）
   
   

すでにこの式は、ここまでの解説で既出であるため、詳細な解説は省きます。
 
 

補足２：複利計算における「7-10ルール」

ここまで見てきた複利ですが、いまいち具体的にどのように利益が増えていくのかイメージができません。

しかし、実は、「7-10ルール」という、

複利計算での元利合計の増え方をイメージする際に役立つルールがあるので見ていきましょう。
 
 

7-10ルールとは、

年利率７％で複利で運用すると大体１０年で２倍になり、

年利率１０％で複利で運用すると大体７年で２倍になりというものです。
 
 

グラフにするとこんな感じでしょうか。

実際に計算してみましょう。
 
 

100USDCを元本で運用した場合を計算してみました。

$$V_{10}=100 \times(1+0.07)^{10}=196.7151357\approx100 \times2$$

$$V_7=100 \times(1+0.10)^7=194.87171\approx100 \times2$$

 
 

確かにほぼ２倍になりますね😊
 
 

補足３：単利と複利の関係性：短期の複利はほぼ単利

では、これまで見てきた複利計算による元利合計をもとに複利と単利の関係を考察していきます。
 
 

ある期間$t$の間に、$n$回複利計算が行われるとします。

まず、複利計算による元利合計は以下です。

$$V_t = P \times (1 + r \times \frac{t}{n})^n$$

 
 

また、単利計算による元利合計は以下です。

$$V_t = P(1+ r t)$$

 
 

ここで、マクローリン展開という便利なものを使います。
 
 

これは、x=0周りに限定して、どんな関数でも多項式に近似できるという優れものです。

微分を重ねる度、精度を向上されます。

$$f(x) = f(0) + f'(0)x + \frac{f''(0)}{2!}x^2 + \frac{f^{(3)}(0)}{3!}x^3 + \dots + \frac{f^{(n)}(0)}{n!}x^n + \dots$$

 
 

今回は、マクローリン展開を用いて、１回分までの荒目の精度を用いて、

$V_t = P \times (1 + r \times \frac{t}{n})^n$の外観を見てみます。
 
 

では、$V_t = P \times (1 + r \times \frac{t}{n})^n$を$t$で微分します。

$$\frac{dV_t}{dt} = P \times \frac{d}{dt} \left\{ (1 + r \times \frac{t}{n})^n \right\}$$

 
 

まず、$u =1 + r \times \frac{t}{n} $とおきます。
 
 

$$\frac{dV_t}{dt} = P \times \frac{d}{dt} \left( u^n \right)$$

$$\frac{d}{dt} \left( u^n \right) = n \times u^{n-1} \times \frac{du}{dt}$$

 
 

次に、$ u = 1 + \frac{r}{n} \times t $ について微分を行います。

$$\frac{du}{dt} = \frac{r}{n}$$

 
 

したがって、全体の微分は次のようになります。

$$\frac{dV_t}{dt} = P \times \frac{d}{dt} \left( u^n \right)$$

$$\frac{dV_t}{dt} = P \times n \times u^{n-1} \times \frac{r}{n}$$

$$\frac{dV_t}{dt} = P \times r \times \left(1 + \frac{r}{n} \times t\right)^{n-1}$$

 
 

この結果から

$$V_t = P \times (1 + r \times \frac{t}{n})^n$$

$$V_t \approx V_0 + \frac{dV_0}{dt}$$

$$V_t \approx P \times (1 + r \times \frac{0}{n})^n+ P \times r \times \left(1 + \frac{r}{n} \times 0\right)^{n-1}$$

$$V_t \approx P + P \times r = P(1+ r t)$$

 
 

したがって、単利計算における元利合計が以下であったことを思い出すと、

$$V_t = P(1+ r t)$$

 
 

開始直後の微小時間経過時の複利計算においては、

単利計算とみなせるという非常に面白い結果が得られました。
 
 

しかし、直感的には当たり前かも...
 
 

締め

非常に長くなってしましましたが、

APR・APYを切り口に、私の中で曖昧だった単利・複利の詳細を整理することができました。
 
 

私の最近の関心事のひとつに、Defi運用における利益をどのように正確に計上するかというものがあります。
 
 

今後、実際にスプレッドシートを叩いて試行錯誤をすると思いますが、

その際得られた知見などは、本ページに都度加筆修正していく予定です。
 
 

完全に素人ですので、本ページの記載に不正確な理解などあれば、ご指摘いただけるとありがたいです。
 
 

これからもよろしくお願いします。
 
 

参考文献

• 金融工学入門 第2版
• Annual Percentage Rate (APR): What It Means and How It Works
• What is an Annual Percentage Rate (APR)?
• ＡＰＲ(年百分率)の概念について
• 利率計算の罠
• APR ⇔ APY 変換公式
• Nominal and Effective Interest
• APR/APY In-Depth Guide For DeFi
• Annual Percentage Rate (APR): What It Means and How It Works
• What Is APY and How Is It Calculated?
• APR vs. APY: What’s the Difference?
• 一瞬の利息ー金利の方程式と連続複利ー
• 一瞬の利息 連続複利と極限値
• 単利は複利の近似 ～１次の近似式