【3部作】これであなたもUniswapV2チョットデキル【前編】:流動性を基軸にUniswapV2モデルとその実装を整理する
導入
経緯
私は、UniswapV2やその派生プロジェクトのコントラクトに対して、
ABI経由で操作するプログラムをプライベートで実装してます。
しかし、安定稼働後の改修に入るタイミングで、
いつもUniswapV2の実装や構成がどうなっていたか細かいところの記憶が曖昧になってしまいます。
そこで、自分のためにも、UniswapV2がそもそもどのようなコンセプトであり、
そのコンセプトをどのように実装しているのか、整理して記録しておくことにしました。
公開した後もより詳しく調べたところは都度追記していきます。
※ コードのコメントはChatGPTの4oモデルで翻訳しています。
理解の道筋
UniswapV2は、美しいコンセプトの集合体のようなものです。
個々のコンセプトはシンプルでありつつも、
そのコンセプトを実現するための全体のシステムはかなり複雑で、
「スワップとは?」「流動性提供とは?」などと個別に確認して行ったところで、
このUniswapV2というシステムの全体像が見えてきません。
少なくとも私には今までずっと見えてこず、
いつもモヤモヤとした曖昧な理解を抱えながら、
UniswapV2やそのフォークのプロジェクトと向き合ってきました。
しかし、このままでは、半端なものしか作れないと感じ、
一貫した切り取り方で全体像の把握を今回試みます。
流動性を基軸に全体を俯瞰する
UniswapV2は、UniswapV1から継承されてきた
2つのトークンの交換を前提とした場合のリザーブ(用語の詳細は後述)と
その量的な制限に関しての数理モデル
というコンセプトをベースに実装されており、
一般的に、UniswapV2の解説と言えば、
このモデルをベースにスワップの説明がなされる記事が多いです。
しかし、スワップの仕組みを理解しても、
「UniswapV2チョットデキルヨウニナッテキタ」と全然なりません。
実際、UniswapV2の実装コードにおいて、
スワップの記述はほんの少しで、
多くは流動性をどう管理するかに中心にあるように思われます。
Defiは、ファイナンスです。
Defiを理解する、Uniswapチョットデキルというのは、
自身の資産管理に役立てるようになることだと思います。
本記事では、その足がかりになるところまでの全体像の理解の助けになることを願っています。
準備
UniswapV2は何が難しいのか
右も左もわからなかった1年前を振り返ってみる
およそ1年ほど前に、某ブロックチェーンゲームのギルドコミュニティにて、
Defiを話題にコミュニティに貢献しようとしたことがありました。

その初期テーマの1つにUniswapV1〜V4を理解するというものがあったのですが、
私の理解力が無さすぎて頓挫しました。
というのも素人がいきなり理解するには難しすぎました。
まず難解だったのは、
UniswapV2の有名な数理モデル
結局どこのコントラクトに実装されているのかというところでした。
このモデルが、何をして、結局どこで実現されているのか全然わからなかったわけです。
また、モデルを仮に理解できたとして、
各基礎トークン(後述)を供給したり(Supply)、引出したり(Withdraw)した場合、
その変化はモデルにどのように還元されるのかというところもわかりませんでした。
ただ、これを成り立たせるには、様々な実装上の工夫が不可欠です。
UniswapV2は、トークンの量を丁寧に管理することでシステムを成立させています。
本記事では、
UniswapV2のモデルに関する理解も深めつつも、
モデルを適切に実現するための実装周りも
トークン量、つまり、流動性sに着目した切り口で丁寧に理解していきます。
UniswapV2の概観
大まかな実装構成
まず、UniswapV2の実装は以下のように2つに分かれています。
(出典:https://github.com/adshao/publications/blob/master/uniswap/dive-into-uniswap-v2-contracts/README.md)
v2-coreにおいて、
UniswapV2に必要な最小限の機能の実装が行われており、
v2-peripheryにおいて、
実際にUniswapV2のアプリケーションで使用する際に必要な機能が実装されています。
先ほど、
v2-coreにはUniswapV2Pairコントラクトという、
UniswapV2の本体とも呼べるコントラクトがあります。
ここで、トークンの量を「実際に」管理しています。
「実際に」とは、このコントラクトは、
管理するトークンをコントラクト内に所有しています。
このトークンを管理しているUniswapV2Pairコントラクトには、
swapメソッドという
-
x \cdot y = k - トークンの転送ロジック
しか存在しません。
つまり、
以下が具体的なswapメソッドです。気になる方は確認してみてください。
後ほどより詳しくみていきますし、基本的にコードの理解はしなくていいと思います。
v2-periphery/contracts /UniswapV2Router02.sol > swapExactTokensForTokens etc.
// this low-level function should be called from a contract which performs important safety checks
// この低レベル関数は、重要な安全性チェックを実行するコントラクトから呼び出されるべきです
function swap(uint amount0Out, uint amount1Out, address to, bytes calldata data) external lock {
require(amount0Out > 0 || amount1Out > 0, 'UniswapV2: INSUFFICIENT_OUTPUT_AMOUNT');
(uint112 _reserve0, uint112 _reserve1,) = getReserves(); // gas savings
// ガスの節約
require(amount0Out < _reserve0 && amount1Out < _reserve1, 'UniswapV2: INSUFFICIENT_LIQUIDITY');
// 流動性が不足している場合のエラーチェック
uint balance0;
uint balance1;
{ // scope for _token{0,1}, avoids stack too deep errors
// _token{0,1}のスコープを限定してスタックが深すぎるエラーを回避
address _token0 = token0;
address _token1 = token1;
require(to != _token0 && to != _token1, 'UniswapV2: INVALID_TO');
// 送信先アドレスが不正な場合のエラーチェック
if (amount0Out > 0) _safeTransfer(_token0, to, amount0Out); // optimistically transfer tokens
// トークンを楽観的に送信
if (amount1Out > 0) _safeTransfer(_token1, to, amount1Out); // optimistically transfer tokens
// トークンを楽観的に送信
if (data.length > 0) IUniswapV2Callee(to).uniswapV2Call(msg.sender, amount0Out, amount1Out, data);
// dataがある場合はコールバックを実行
balance0 = IERC20(_token0).balanceOf(address(this));
balance1 = IERC20(_token1).balanceOf(address(this));
}
uint amount0In = balance0 > _reserve0 - amount0Out ? balance0 - (_reserve0 - amount0Out) : 0;
uint amount1In = balance1 > _reserve1 - amount1Out ? balance1 - (_reserve1 - amount1Out) : 0;
require(amount0In > 0 || amount1In > 0, 'UniswapV2: INSUFFICIENT_INPUT_AMOUNT');
// 入力トークン量が不足している場合のエラーチェック
{ // scope for reserve{0,1}Adjusted, avoids stack too deep errors
// reserve{0,1}Adjustedのスコープを限定してスタックが深すぎるエラーを回避
uint balance0Adjusted = balance0.mul(1000).sub(amount0In.mul(3));
uint balance1Adjusted = balance1.mul(1000).sub(amount1In.mul(3));
require(balance0Adjusted.mul(balance1Adjusted) >= uint(_reserve0).mul(_reserve1).mul(1000**2), 'UniswapV2: K');
// Kのチェック
}
_update(balance0, balance1, _reserve0, _reserve1);
// リザーブを更新
emit Swap(msg.sender, amount0In, amount1In, amount0Out, amount1Out, to);
// スワップイベントを発行
}
では、swapといういかにも
一体どこにあるのかという話になりますが、
具体的には、
v2-peripheryのUniswapV2Router02コントラクトに記述された、
例えば、swapExactTokensForTokensメソッド内から呼び出される、
UniswapV2LibraryコントラクトのgetAmountOutメソッドなどに実装されてます。
以下にそれぞれのコントラクトの該当箇所を紹介しておきます。
v2-periphery/contracts /UniswapV2Router02.sol > swapExactTokensForTokens etc.
// **** SWAP ****
// requires the initial amount to have already been sent to the first pair
// **** スワップ ****
// 最初のペアに初期の金額が既に送信されている必要があります
function _swap(uint[] memory amounts, address[] memory path, address _to) internal virtual {
for (uint i; i < path.length - 1; i++) {
(address input, address output) = (path[i], path[i + 1]);
(address token0,) = UniswapV2Library.sortTokens(input, output);
uint amountOut = amounts[i + 1];
(uint amount0Out, uint amount1Out) = input == token0 ? (uint(0), amountOut) : (amountOut, uint(0));
address to = i < path.length - 2 ? UniswapV2Library.pairFor(factory, output, path[i + 2]) : _to;
IUniswapV2Pair(UniswapV2Library.pairFor(factory, input, output)).swap(
amount0Out, amount1Out, to, new bytes(0)
);
}
}
// swapExactTokensForTokens
// swaps an exact amount of input tokens for as many output tokens as possible
// swapExactTokensForTokens
// 正確な量の入力トークンをできるだけ多くの出力トークンに交換します
function swapExactTokensForTokens(
uint amountIn,
uint amountOutMin,
address[] calldata path,
address to,
uint deadline
) external virtual override ensure(deadline) returns (uint[] memory amounts) {
amounts = UniswapV2Library.getAmountsOut(factory, amountIn, path);
require(amounts[amounts.length - 1] >= amountOutMin, 'UniswapV2Router: INSUFFICIENT_OUTPUT_AMOUNT');
TransferHelper.safeTransferFrom(
path[0], msg.sender, UniswapV2Library.pairFor(factory, path[0], path[1]), amounts[0]
);
_swap(amounts, path, to);
}
v2-periphery/contracts/libraries /UniswapV2Library.sol > getAmountOut, getAmountIn
// given an input amount of an asset and pair reserves, returns the maximum output amount of the other asset
// ある資産の入力額とペアのリザーブを与えられた場合、他の資産の最大出力額を返します
function getAmountOut(uint amountIn, uint reserveIn, uint reserveOut) internal pure returns (uint amountOut) {
require(amountIn > 0, 'UniswapV2Library: INSUFFICIENT_INPUT_AMOUNT');
require(reserveIn > 0 && reserveOut > 0, 'UniswapV2Library: INSUFFICIENT_LIQUIDITY');
uint amountInWithFee = amountIn.mul(997);
uint numerator = amountInWithFee.mul(reserveOut);
uint denominator = reserveIn.mul(1000).add(amountInWithFee);
amountOut = numerator / denominator;
}
// given an output amount of an asset and pair reserves, returns a required input amount of the other asset
// ある資産の出力額とペアのリザーブを与えられた場合、他の資産の必要な入力額を返します
function getAmountIn(uint amountOut, uint reserveIn, uint reserveOut) internal pure returns (uint amountIn) {
require(amountOut > 0, 'UniswapV2Library: INSUFFICIENT_OUTPUT_AMOUNT');
require(reserveIn > 0 && reserveOut > 0, 'UniswapV2Library: INSUFFICIENT_LIQUIDITY');
uint numerator = reserveIn.mul(amountOut).mul(1000);
uint denominator = reserveOut.sub(amountOut).mul(997);
amountIn = (numerator / denominator).add(1);
}
結論として、以下が
v2-periphery/contracts/libraries /UniswapV2Library.sol > getAmountOut, getAmountIn
uint amountInWithFee = amountIn.mul(997);
uint numerator = amountInWithFee.mul(reserveOut);
uint denominator = reserveIn.mul(1000).add(amountInWithFee);
amountOut = numerator / denominator;
初心者は、全くなぜこれが
ほんと、こんなのわかるわけないです😂
このように
プログラミングの素養がない人にとっては迷路のようになっています。
Defiユーザーの大半は、コードが読めないと思いますし、
さらには、初心者となるとわかるわけがありません。
UniswapV2は、やはり初心者にはかなり難しいと思います。
かつての私も全く理解できませんでした。
初心者向けの解説記事では、
その詳細が不明であり、結局、運用やヘッジに利用するまでの理解を得られません。
なので、この記事は、当時の私でも理解できるような、
コードのソースを記載しながらも、
コードを読めなくても何となくUniswapV2が理解できるような、
また、現在では、
UniswapV2やその系列単体で運用することはあまりないと思いますが、
LPを利用したプロジェクトを少し理解して運用検討の一歩目の直前までは
整理して提供できればと考えています。
用語の整理
では、前置きが長くなってしまいましたが、
具体的な話に移っていきます。
あらかじめ、混乱を避けるため、あらかじめ本記事で使用する用語は整えておきます。
明確な間違いがあるかもしれませんので、その際はご指摘いただけますとありがたいです。
まず、よくクリプト界隈、Web3界隈で
「スマコン」という言葉がよく使われますが、
これを「コントラクト」と捉え、
『
「特定のアドレス」を持っている、
「状態」と「状態を操作するもの」をセットで持っている情報の構造、
または、その構造を有するもの
』
という意味で使用させていただきます。
先ほど使用していた、メソッドというのは、「状態を操作するもの」のことを言います。
プログラミングにおける「関数」という言葉を知っている方は、
「関数」と理解していただいて構いません。
また、「トークン」という言葉もありますが、これは、
『
ERC20という規格に準拠した誰でも作成可能な貨幣のようなもの
』
としておきます。
UniswapV2では、
2つのトークン量の情報をコントラクトの「状態」に記録し、
「状態を操作するもの」を使用してスワップを実現しています。
言い換えると、トークンの交換を実現しています。
UniswapV2がトークンの交換を実現しているコントラクトにおいて、
このコントラクトの状態に記録された2つの各トークンの量を「リザーブ」、
このコントラクト自体を抽象的に「ペア」と呼びますし、「プール」ともいいます。
後者の場合は、トークンが貯まっている、リザーブが貯まっているという
意味合いが強いと思います。
また、2つのトークンを合わせて「ペア」ともいいます。
「リザーブ」について、補足しますと、
「リザーブ」は、
UniswapV2Pairコントラクトにおける2つのトークンの「残高、バランス(balance)」とほぼ同じです。
UniswapV2Pairコントラクトが持っているお財布の中の残高というイメージです。
より正確にいうと、「残高、バランス(balance)」の方が、敏感に変動します。
後述しますが、「リザーブ」「残高、バランス(balance)」はコードで明確に区別され、
UniswapV2のシステムの弱点とならないように配慮されています。
ここまでの用語を、抽象的に言い換えると、
「ペア」は「リザーブ」として「プール」に預けられているというイメージです。
また、このトークンの交換を実現しているUniswapV2Pairコントラクトである、
「ペア」「プール」自身もトークンです。
つまり、
2つのトークンを管理しているトークンが存在し、
そのトークンはコントラクト(UniswapV2Pairコントラクト)であり、
そのコントラクトがUniswapV2の機能を実現しています。
ややこしい...
以下にまとめておきます。
-
コントラクト:
- 「特定のアドレス」を持っている、「状態」と「状態を操作するもの」をセットで持っている情報の構造、または、その構造を有するもの。
-
トークン:
- ERC20という規格に準拠した誰でも作成可能な貨幣のようなもの。
- ERC20という規格をもとにトークンが作成されることで、各Defiプロジェクトは、各トークンの規格をいちいち意識しないで、トークンを絡めたアプリケーションを実装できます。
- 規格とは具体的にいうと、コントラクトで説明した「状態」と「状態を操作するもの」をあらかじめ決定しておき、その実現ルールを決めたものと理解すればいいと思います。
-
プール(流動性プール):
- UniswapV2 Pairコントラクトのことを抽象的にいっている気がしています。
- より正確には、UniswapV2 Pairコントラクトのインスタンスです。
- リザーブの言い換えのこともある気がします。
- いずれにせよ、2つのトークンが何らかの入れ物に貯まっているイメージです。
-
ペア:
- UniswapV2 Pairコントラクトのこと。
- これも正確には、UniswapV2 Pairコントラクトのインスタンスだと思います。
- プールを構成する2つのトークンのこと。
-
リザーブ:
- プールを構成している、コントラクトの状態に記録されている各トークンの量。
- もっと具体的にいうと、UniswapV2Pairコントラクトで記録されている「状態」。
- 「プールに預けられているトークンの量」とも抽象的に言い換えられる。
- UniswapV2Pairコントラクトが保持している残高とほぼ同じ。
-
(特定のプールにおける)価格:
- リザーブの比
- 正の値。
-
流動性:
- UniswapV3において明確になってきますが、
x \cdot y = k k - より正確には、
k \sqrt{k}
- UniswapV3において明確になってきますが、
-
流動性提供者(liquidity provider, LP):
- UniswapV2は、AMMですが(後述)、流動性を提供するユーザーが存在して初めて機能します。この流動性を提供するユーザーを、流動性提供者、liquidity provider、略して、LPといいます。
-
基礎トークン(underlying token):
- 基礎トークンという訳が適切かわかりませんが、本記事ではこの表現を使わせていただきます。
- プールを構成するトークンであり、underlying asset という表現で記述されています。
- underlyingという言葉は、そもそもデリバティブ(原資産から派生した商品、金融派生商品)の文脈で使われるのではないかと思います。(詳しい方教えて下さい。)
- 後述のLPトークンは、基礎トークンを原資産とするデリバティブでしょう。
理解する上で抑えるべきポイント
以下の点を押さえておけば、理解の助けになるかと思います。

(出典:https://github.com/adshao/publications/blob/master/uniswap/dive-into-uniswap-v2-contracts/README.md)
- v2-peripheryのコントラクトからv2-coreのコントラクトの「状態を操作するもの」(関数、メソッド)を実行するという流れがある
- 流動性&\sqrt{k}&が一定である場合に、数理モデル
x \cdot y = k - 流動性が変動する場合に、
\sqrt{k} - 流動性の変動、つまり、&\sqrt{k}&の変化と
x \cdot y = k - コントラクトが持っているトークン残高を前提とするロジックは見落としやすい
では、そろそろ本題に入っていきましょう。
本題
UniswapV2のシステムは、AMMというカテゴリに分類されます。
まずは、AMMをざっくりと理解して、Uniswapの全体像を掴む足掛かりとします。
AMM(Automated Market Maker)
トークンの交換:オーダーブック(板)とAMM
Uniswapとは、その名の通り、任意のトークンのスワップ、
つまり、交換を実現したDefiプロジェクトです。
さらに、正確に表現すると、
Uniswapは、分散的な交換を実現したDEX(Decentralized Exchange, 分散型取引所)で、
板取引をベースとしたものではない、
AMM(Automated Market Maker)という設計での交換を実現したものです。
特定のアルゴリズム(ロジック、ルール)で自動的に価格を決定し、
いつでも基礎トークンを取引可能にしたシステムがAMMです。
AMMという設計では、
オーダーブックを用いて(板取引)トークンを提供する他の「人」と交換するわけではなく、
(Uniswapのような)システムのルールに従い、
トークンが集められているプールを取り扱う「システム」を相手に交換します。
-
AMM補足1:オーダーブックベースとAMMベースの関係性の補足資料
The History of dYdX (so far)
オーダーブックをベースとしたdYdXが、AMMベースのUniswapV2に、一時、取って代わられた話はとても興味深いです。Defi分野におけるAMMの影響が垣間見えるかと思います。 -
AMM補足2:マーケットメイカーとはそもそも何か?
以下のポッドキャストを聴くとイメージできるかと思います。
https://podcasters.spotify.com/pod/show/miharablt/episodes/25--12-e2apd46/a-aageokj
https://podcasters.spotify.com/pod/show/miharablt/episodes/26---22-e2auc5p/a-aaguk7p -
AMM補足3:AMMの文脈でのマーケットメイカー・メイキングに関する整理
以下の資料が非常に参考になります。
マーケットメイカー・メイキングに関しては、私自身言及できるほど詳しくないので、
資料にて整理願います。
https://nightlycrypto.medium.com/what-the-heck-is-an-automated-market-maker-amm-3adb753ea5c7
UniswapV2をAMMという表現で括るのは大雑把過ぎますので、より詳細に定義しておくと、
DEX
-> Automated Market Maker(AMM)
->> Constant Function Market Maker (CFMM)
->>> Constant Product Market Maker (CPMM)
->>>> UniswapV2
という位置付けにあります。
-
DEX補足:DEX発展の流れ
- 過去に、A Brief History of Decentralized Exchangeの記事内の画像を編集し、以下の発展の流れの図を作成しました。(原本は先日HDDを落下させ天に召されました。)

- 過去に、A Brief History of Decentralized Exchangeの記事内の画像を編集し、以下の発展の流れの図を作成しました。(原本は先日HDDを落下させ天に召されました。)
では、より理解を深めるため、AMMにおけるトークン価格について見ていきましょう。
AMMのトークン価格の捉え方
AMMにおけるトークンの価格とはなんでしょうか。
そもそも価格とは何でしょうか。
例えば、1 USD = 144.37 YEN(8月25日 3:19 UTC)
は1ドルで買える日本円の量と捉えられます。
つまり、価格は交換における、
1単位となるもの(今回だとUSD、これが、リンゴとかでもいい)で取得できる
ペアとなる相手方の量を決めたルールです。
さらにいうと、どちらかを1としたときの量の比です。
話を戻します。
AMMにおけるトークン価格について整理する上で、
比較的わかりやすいオーダーブックを参考に比較しながら考えていくが良さそうです。
まず、オーダーブックでは、この量の比の値を提示しあって、
売りと買いの参加者が提示する価格がマッチするポイントが、
決定された量の比、
つまり、トークンの価格といえそうです。
そして、
「売りと買いの参加者が提示する量の比がマッチするポイントで取引を確定する」
といった取引における取り決めがあります。
では、AMMの場合は、どのような取り決めがあり、どのように価格が決定されるのでしょうか。
まず、AMMにおける取引の取り決めですが、相手が人間ではなく、システムである以上、
取引を確定する際のルールを前もって決めておいて、
そのルールをもとに自動的に動くようにしておく必要がありそうです。
そのルールを自動的に実行していき、その実行時の交換量の比が価格といえるでしょう。
ここで、具体例を用いながらこの前提ルールを考えていきましょう。
仮に、MyToken(MTK)というオリジナルのトークンがあったとして、
このトークンの価格を考えてみることにします。
交換を前提とするため、
ひとまずは、USDCとの比較において、MTKの価格を考えます。
例えばですが、
MTKとUSDCが物理的なコインだとして、適当な量がボトルに入っていたとしましょう。
あなたは、このボトルの管理者であり、
人々がこのボトルの中を交換する際は、あなたを介して行います。
この前提のもと、
ボトル中の量でのみ(前提とする系でのみ)MTKとUSDCの交換が可能だとして、
あなたは、ひとまず、MTKとUSDCの価値がよくわからないので、
ボトルの中の量の比で、なんとなくの交換比を決定することにしました。
そして、人々が、そのボトルの中のMTKとUSDCを
「1MTKは大体10USDCぐらいのものを買えそうだ!」とか、
「いやいや、20USDCは下らないだろ!」とか、
考えながら交換を続けるとします。
もっと抽象的に言えば、
自身の考えよりもMTKを割安で買えるなら、その人はMTKを購入するでしょうし、
自身の考えよりもMTKを割高で売れるなら、その人はMTKを売却するでしょう。
上記のように交換が続けられると、
短い期間では、MTKとUSDCの量は、およそ一定の範囲内で固定されていきそうです。
このように考えてみると、
固定された量の比がAMMのトークンの「価格」と言えそうではないでしょうか?
数理モデルx \cdot y = k
さて、ここで具体的なルールが必要となってきます。
先ほどの考察では、重要な前提が明言されていませんでした。
それは、「ボトルの中が空にならない」
つまり、ボトルの中の基礎トークンは有限であるはずなのに、
どちらのトークンも失われない前提で話をしていたということです。
有限であるという前提を加味した場合、
交換によって、基礎トークンのどちらか増えると、相方のトークンは減るわけですから、
MTKというわけのわからないトークンは、誰も価値を感じずに、
すぐにUSDCに交換するでしょう。
そして、ひたすら交換され続けたUSDCは減っていき、
最終的には、ボトルのUSDCは枯渇してしまうでしょう。
そうなるとMTKとUSDCは交換できなくなるため、この交換ボトルは死を迎えます。
あなたは管理者として失格となりますね。
このように、死んでしまう前提で交換の場を作ってしまうと、
この仕組み(AMM)はそもそも成り立ちません。
したがって、どうにかして枯渇しない仕組み、ルールを導入しなければなりません。
つまり、どちらかの量が増えると、
相方のトークンの取得難易度が動的に変更されるようなルールが必要になりそうです。
まとめると、
取得難易度である価格が、売り手の思考をベースとするオーダーブックとは違い、
システムであるAMMは、
アルゴリズム、ルール、数式で動的に変化するよう決めておく必要があります。
ここまで、具体的な量を決めずに、定性的に話を進めて来ましたが、
ここからは、具体的な数字を扱った定量的な議論をするために、
ボトルの中のMTKの量を
では、先ほど言及した、
アルゴリズム、ルール、数式といったところを具体的に数値が導いていける形で考えてみましょう。
つまり、トークンの取得難易度を考慮した、
ボトル内のトークン量を決定する数理モデルを考えます。
まずは、価格が常に1:1の関係である、
つまり、取得難易度に動的な変更がない
最も簡単な数理モデルを考えてみましょう。
この最も簡単な数理モデルは、
の数式をもとに考えられます。
ボトルの中のトークンの量を
ボトルの中身だけで見ると
となるルールを満たすため、
ここで、
ボトルの中の
ボトルの中の
となることから
この条件から
となります。
整えると、以下のようになります。
具体的に確認してみると、
例えば
25USDCが排出され、ボトル内は、75USDCになります。
もちろんこのときの
以上をグラフにすると以下のようになります。
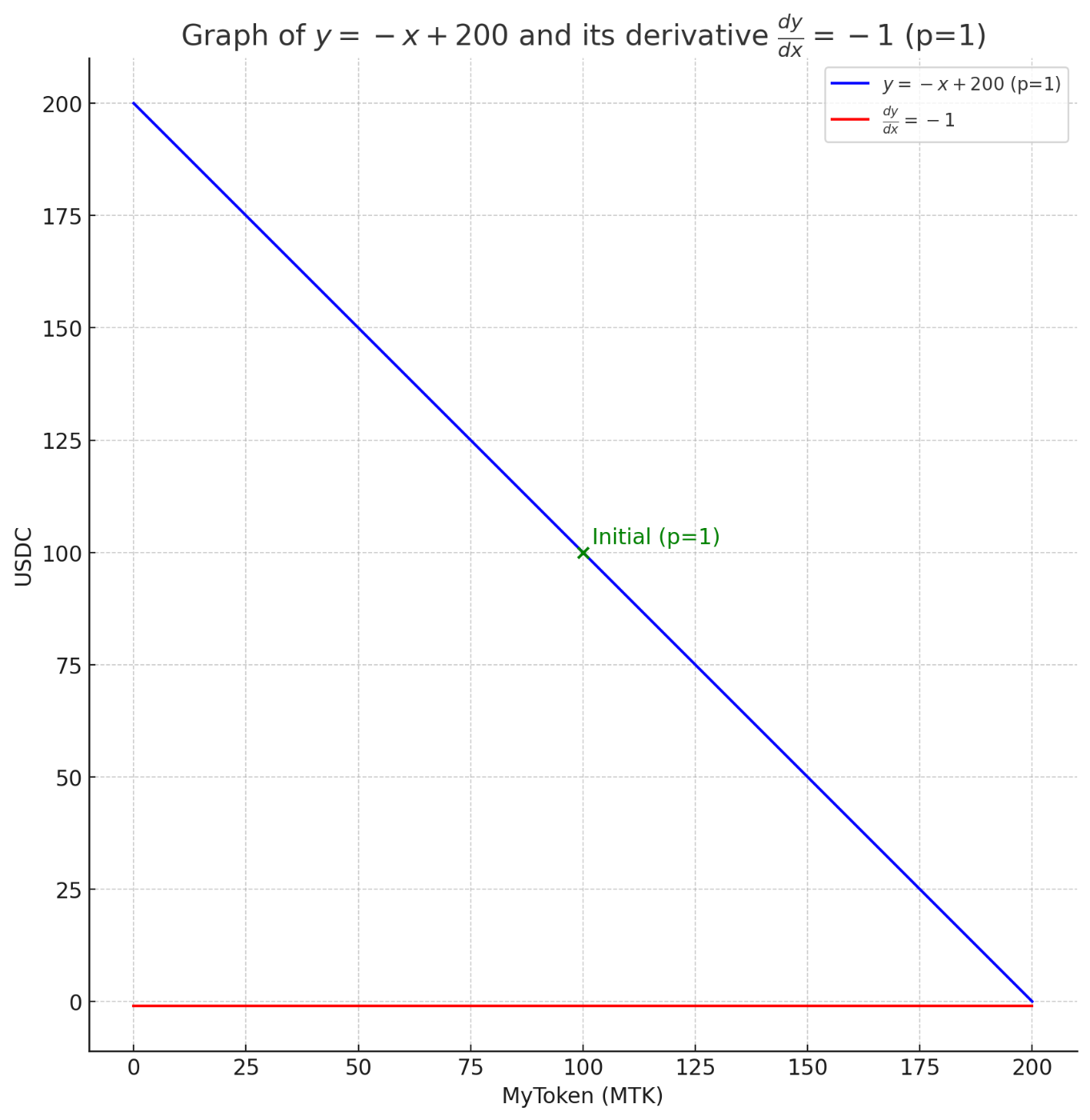
青線はボトルの中のトークンの量が
赤線はトークン同士の取得難易度(交換比、価格)を表しています。
今回は常にその難易度(交換比)は-1である様子を赤線で示しています。
まあ、これは、正にすると価格と同じ意味です。
また、この難易度が動的に変わらない、静的なものとして、
1:1ではない、1:5である場合のグラフが以下になります。
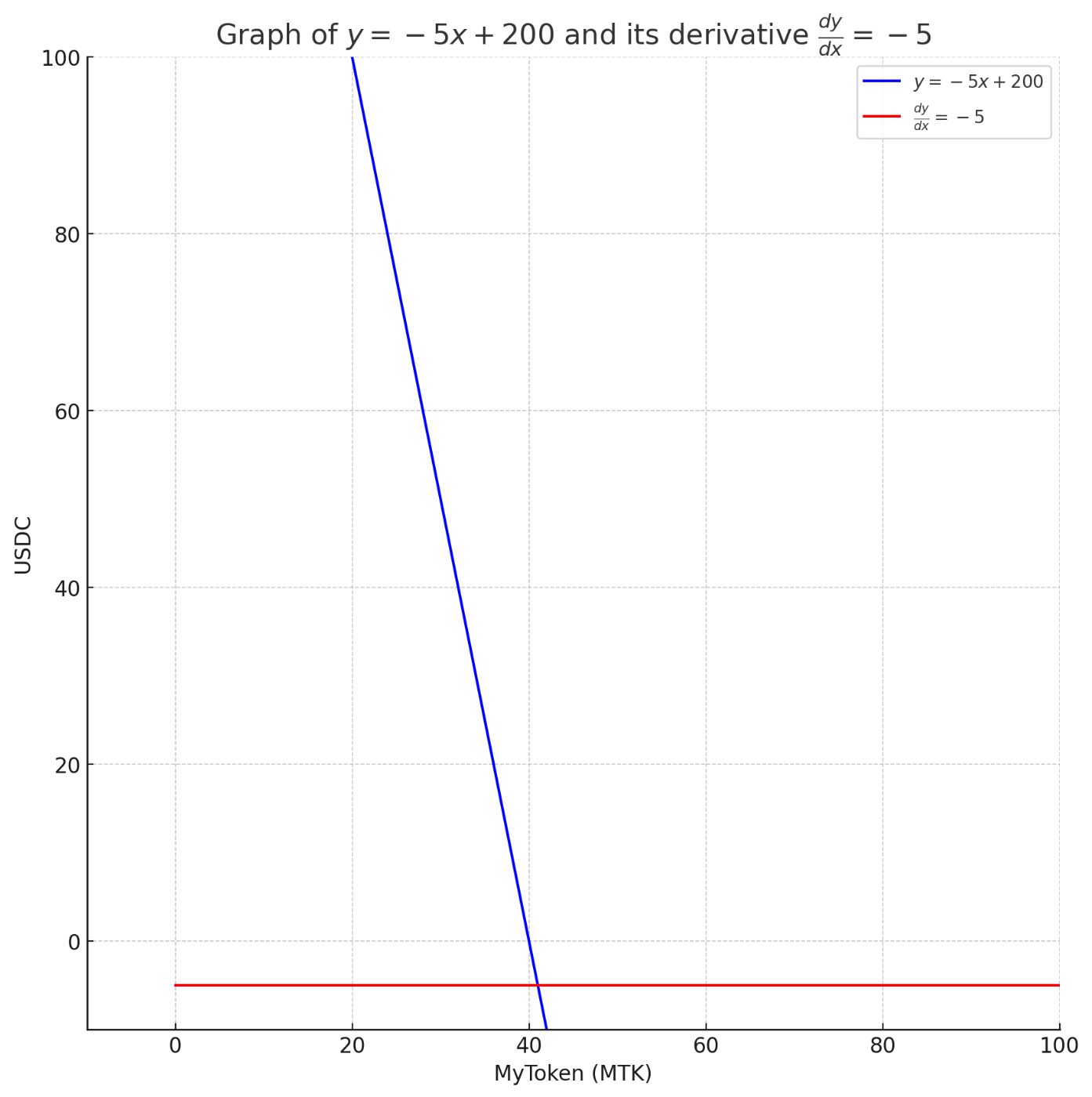
さて、これらのグラフは、
価格の変化なし、取得難易度の変化なしでスワップを続けると、
ボトル内のどちらかのトークンの量が
では、
AMMの取引のルール、価格決定のルールを決めようとしている今、
枯渇しないようなモデルはどうすれば作れそうでしょうか?
その前に、まず、先ほどの価格を固定した場合の数理モデルをより丁寧に噛み砕いてみてみましょう。
こちらが先ほどの数理モデルを一般化したものです。
このモデルの傾きは、
これにマイナスを乗じると、
つまり、
xを1つ獲得するために、どれだけyをマイナスする必要があるかを表しています。
より専門的に記載すると以下のようになります。
先ほどの具体例で言えば、
$p = 1 $ですので、結果は次の通りです、
はい。では、忘れそうでしたので、今何してたかと言いますと
AMMにおける、
「取引を確定する際のルールを前もって決めておく」
「そのルールをもとに自動的に動くようにしておく必要がある」
「ルールを自動的に実行していき、その実行時の交換量の比が価格といえる」
「枯渇しないようなモデルはどうすれば作れそうか?」
という話でした。
つまり、
青のグラフが0にならないものを作りたいですし、
今言及した、
つまり、赤線の
この2つの条件の時点で何となく、
青グラフは、曲線を使いたくなってきます。
しかも、
さらに、
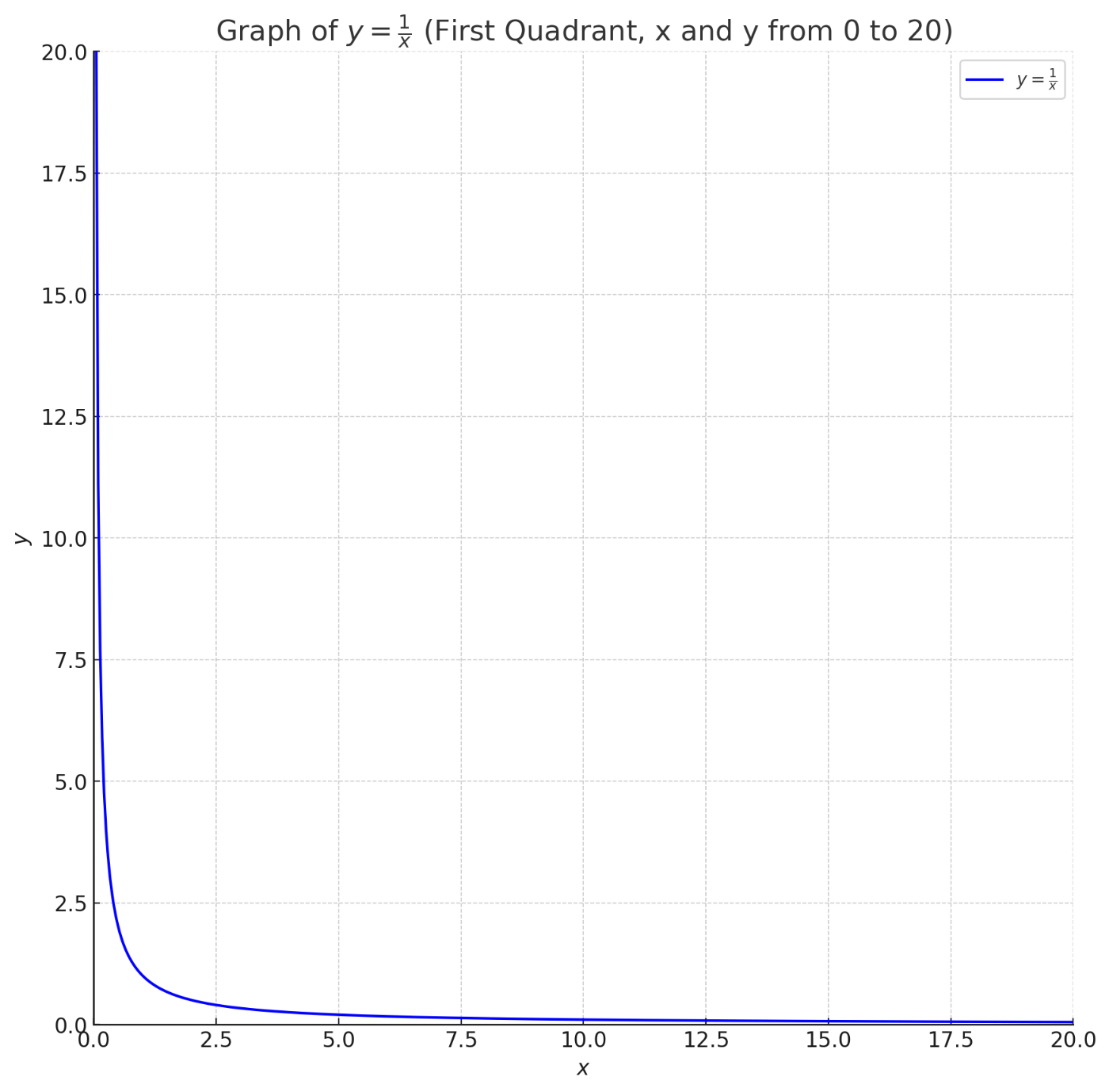
第一象限(
とすると
という曲線が候補にあがりそうに思いませんか?
グラフを見るとまさに、ピッタリ。
また、
において、分子の値の平方根の値(幾何平均)が、
凸部分の
つまり、この座標
こちらもイメージを助けてくれそうです。
したがって、以下のようなイメージでしょうか。
ということで、かなり強引ではありますが、
このような流れを経て、UniswapV1, V2は、
の採用に至ったのではと考察することもできます。
さらに、深堀ります。
本当に、
しかも、トークンが少なくなるほどそのトークンの取得が難しくなっているのか
確認してみましょう。
イメージとしては、以下でしょうか?
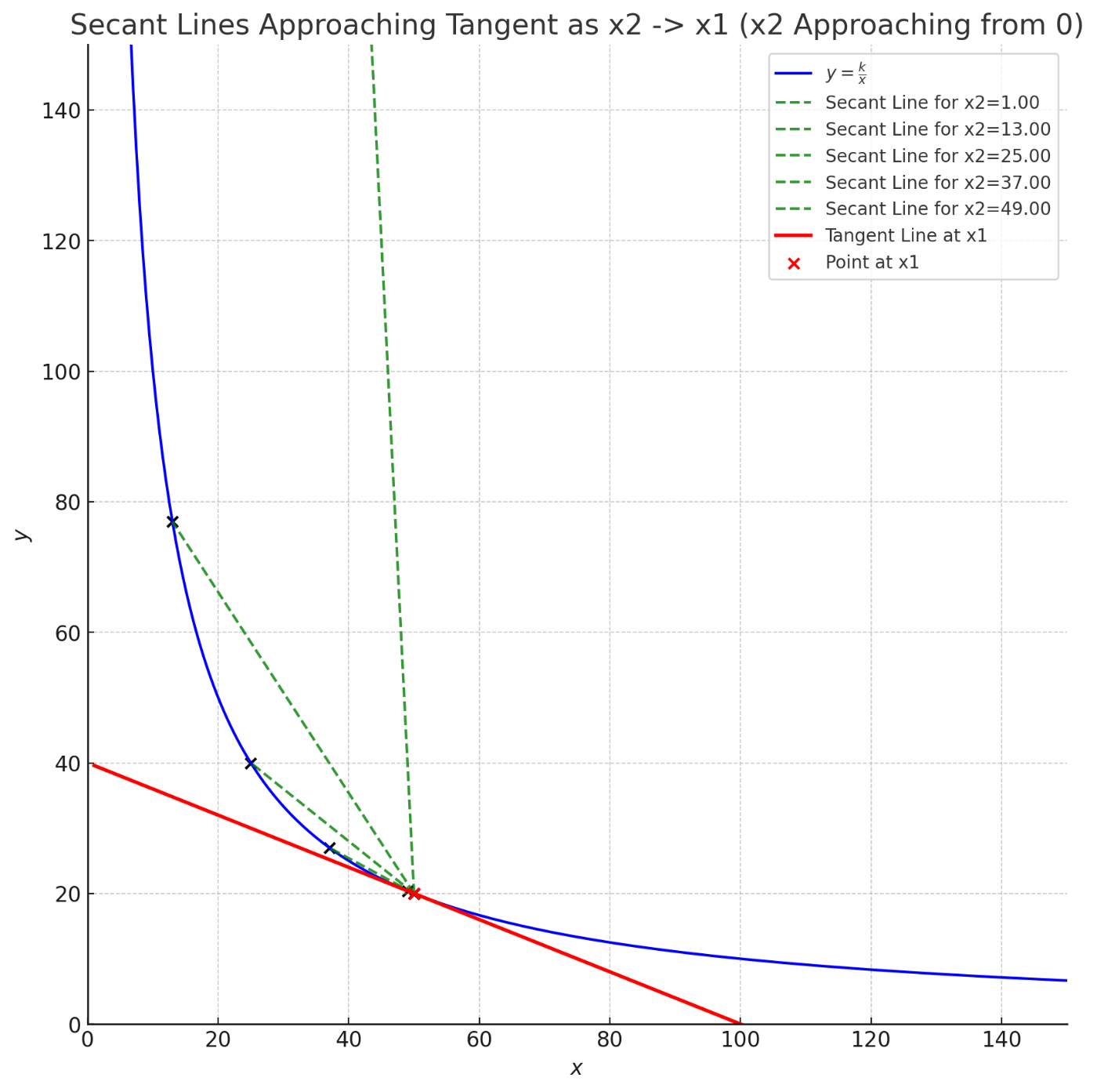
赤と緑の直線です。
赤❌の地点から黒✖️の地点に移動するとみます。
最初、赤❌にMTKとUSDCがあった場合から、
各黒✖️に移動(
これは
のマイナスの値が大きくなっていることを意味しています。
つまり、
ちゃんと取得難易度が動的に上がっています。
正確には、以下のようになります。
この式を
ここで、
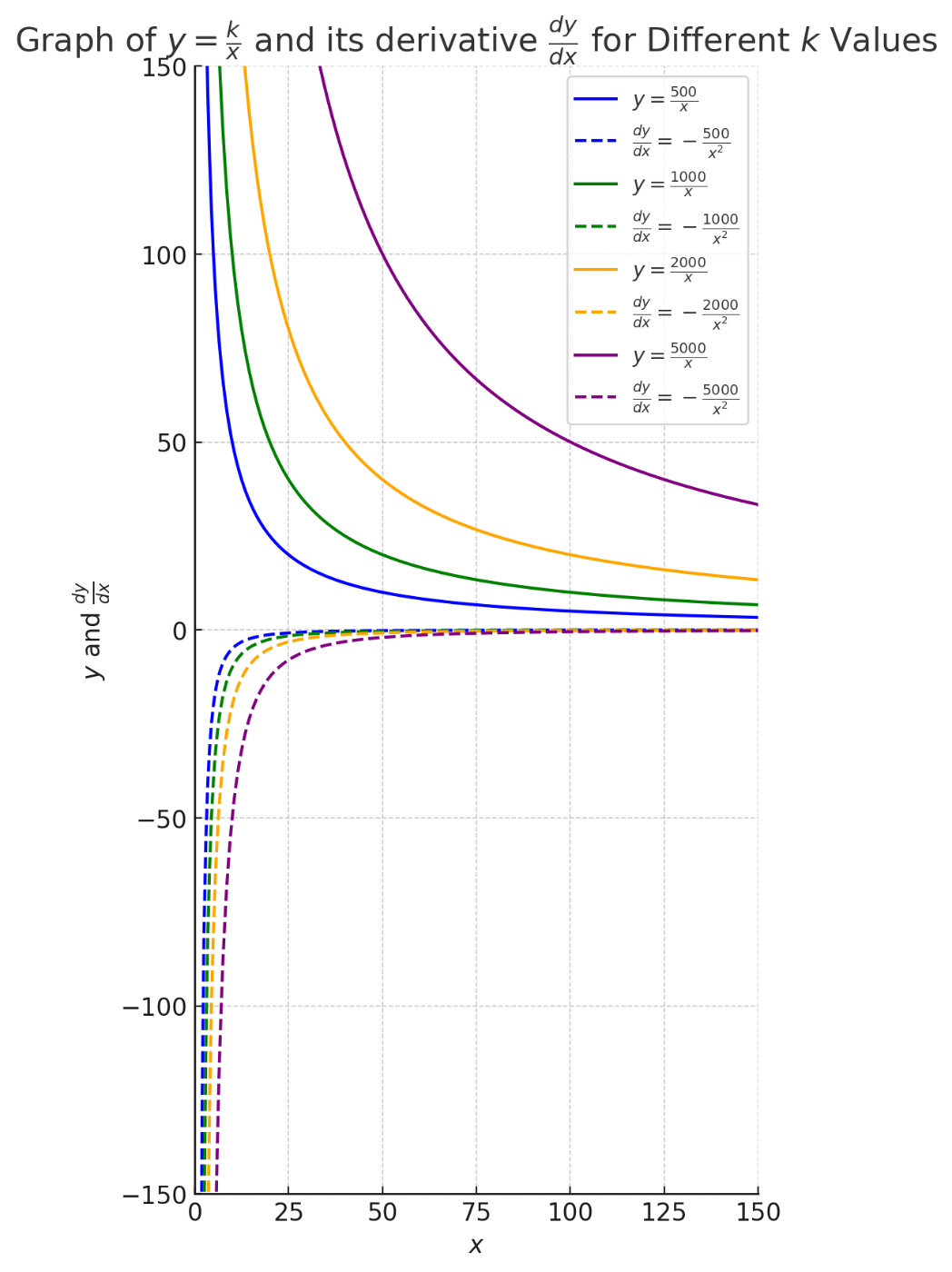
グラフとしては、以下です。
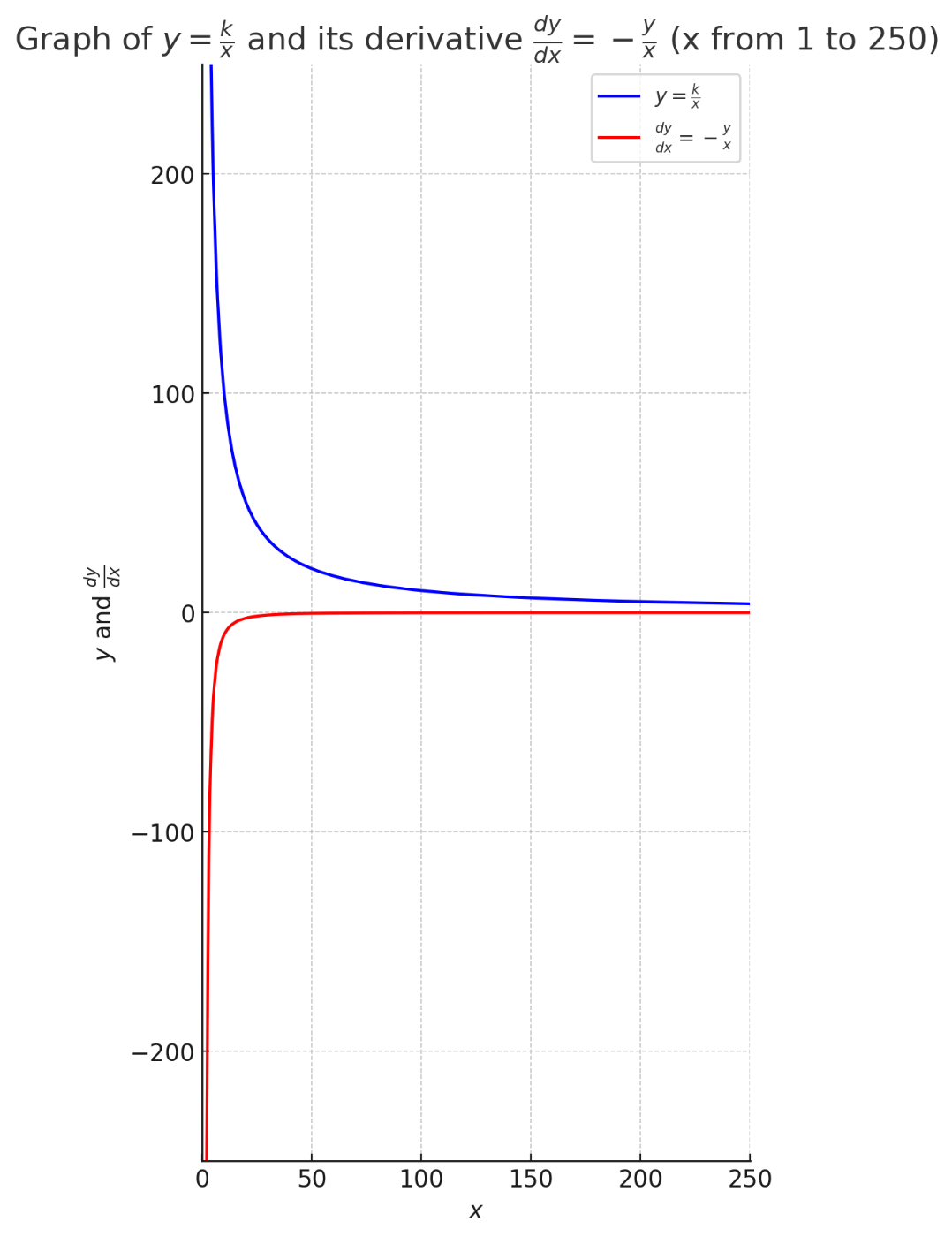
青色の線が元の曲線 $y = \frac{k}{x} $ を表しており、
赤色の線がその微分
また、微分の考え方は、先ほども使用した、
以下のグラフがイメージの助けになりますので、再度掲載しておきます。

では、ここまでのことを最後にまとめて、次の話題に移ります。
ここまで、オーダーブックと比較とボトルという例えを手がかりとして、
AMMにおける、
「取引を確定する際のルールを前もって決めておく」
「そのルールをもとに自動的に動くようにしておく必要がある」
「ルールを自動的に実行していき、その実行時の交換量の比が価格といえる」
「枯渇しないようなモデルはどうすれば作れそうか?」
という話題を考えて来ました。
斬新なアイデアや0から1を実現するときに、
シンプルでパラメータの少ない数理モデル採用したいものです。
Uniswapもその例で、
ボトルの中に限定した量をもとに価格、取得難易度を決め、
その取得難易度は、ボトル内が
の採用に至り、枯渇しないようなモデルを実現したと推測されます。
そして、これをイーサリアムのブロックチェーン(EVM)に配置(デプロイ)して、
ユーザーのトレード要求に答える相手として実現しました。
現状、この最もシンプルなモデルは改良され、
Uniswapの後継バージョン、Curveなどの別プロジェクト等で改善を重ねられています。
非常に長くなりましたが、
は空からアイデアが降って来たわけではなく、
順に必要なことを整理していった結果の産物であると言えます。
ここまでは、
つづいては、
一度、主要なコントラクトの詳細を確認し、準備を整えた上で、
さらに
主要なコントラクトの大まかな役割
UniswapV2Pairコントラクト
さて、ここまででAMMやUniswapV2の思想的なところを見てきました。
したがって、ある程度UniswapV2を理解していく上でのベースが整ったと言えます。
先ほど
Uniswapとは、その名の通り、任意のトークンのスワップ、
つまり、交換を実現したDefiプロジェクトです。
と述べましたが、
このスワップを実現するための中心を担うのが、UniswapV2Pairコントラクトです。
(全コードはこちらで確認ください:UniswapV2Pair.sol)

(出典:https://github.com/adshao/publications/blob/master/uniswap/dive-into-uniswap-v2-contracts/README.md)
UniswapV2をWebアプリケーションで経由で皆さん利用しているかと思いますが、
その各機能のエッセンスが詰まったコアロジックが
ここに記載されていると考えていただいて良いと思います。
逆に、Webアプリケーションの各機能を実装しているのは、
後述のUniswapV2Router02コントラクトです。
このコントラクトの役割としては、UniswapV2で必要な計算を色々やってあげて、
その結果本当に必要なものをUniswapV2Pairコントラクトに渡しているようなイメージになります。
UniswapV2Pairコントラクトに話を戻しますが、
実際の基礎トークンの残高などを管理しているのがこのコントラクトでもあります。
皆さんがいつもMetamask(最近の私はRabby Wallet派)などで使用しているアドレス
(外部所有アカウント、EOA、Externally Owned Account、)と同様に、
コントラクトのアドレスでもトークンを所有できます。
また、UniswapV2Pairコントラクトは、ERC-20を拡張した形になっており、トークンです。
つまり、トークンを保持して管理しているトークンがUniswapV2Pairコントラクトです。
入れ子のようになっているとイメージしてください。(まさに、デリバティブという印象)
この後、流動性に話を移していきますが、
あらかじめ流動性について説明しておきますと、
ユーザーがプールに預けるトークンの量のことを流動性(liquidity、リクイディティ)といいます。
より正確には、ユーザーがUniswapV2Pairコントラクトに預けるトークンの量のことです。
したがって、全てのユーザが預けたその流動性(とスワップによる手数料を合わせたもの)が
このコントラクトアドレスの所持分であるといえます。
UniswapV2Router02コントラクト

(出典:https://github.com/adshao/publications/blob/master/uniswap/dive-into-uniswap-v2-contracts/README.md)
では、先ほど少し言及しましたが、
UniswapV2Router02コントラクトについても簡単に整理しておきます。
逆に、Webアプリケーションの各機能を実装しているのは、
後述のUniswapV2Router02コントラクトです。
とすでにお話ししましたが、
例えば、Webアプリケーションで、
インプットするトークンと量を指定するとアウトプット量が把握できたり、
逆に、アウトプットするトークンと量を指定するとインプット量が把握できたりするのは、
このコントラクトの以下のメソッド群のおかげです。
v2-periphery/contracts /UniswapV2Router02.sol
// **** LIBRARY FUNCTIONS ****
function quote(uint amountA, uint reserveA, uint reserveB) public pure virtual override returns (uint amountB) {
return UniswapV2Library.quote(amountA, reserveA, reserveB);
}
function getAmountOut(uint amountIn, uint reserveIn, uint reserveOut)
public
pure
virtual
override
returns (uint amountOut)
{
return UniswapV2Library.getAmountOut(amountIn, reserveIn, reserveOut);
}
function getAmountIn(uint amountOut, uint reserveIn, uint reserveOut)
public
pure
virtual
override
returns (uint amountIn)
{
return UniswapV2Library.getAmountIn(amountOut, reserveIn, reserveOut);
}
function getAmountsOut(uint amountIn, address[] memory path)
public
view
virtual
override
returns (uint[] memory amounts)
{
return UniswapV2Library.getAmountsOut(factory, amountIn, path);
}
function getAmountsIn(uint amountOut, address[] memory path)
public
view
virtual
override
returns (uint[] memory amounts)
{
return UniswapV2Library.getAmountsIn(factory, amountOut, path);
}
また、その実行や、流動性の提供、解除も
このコントラクトがもっているメソッドを実行することで実現できます。
基本的には、このUniswapV2Router02コントラクトで実行した情報が、
UniswapV2Pairコントラクトに渡されることで、
システムが稼働していきます。
流動性と価格(取得難易度)
流動性とは何か...そして価格(取得難易度)への影響
さて、ここまで、
というモデルを雑に構築し、価格について考察してきましたが、
続いては、
私は、
そもそも流動性とは何かというと、すでに言及した通り、
ユーザーがプールに預けるトークンの量のことです。
より正確には、
ユーザーがUniswapV2Pairコントラクトに預けるトークンの量のことです。
流動性の話と来れば、
やっと流動性提供者、LP、LPトークンの話!
如何に流動性を提供していくか!
という話題から始めたいところですが、
ちょっと難しくなりすぎそうなので、
ここまで話して来たグラフの延長線上から整理を進めてみましょう。
まず、先ほど丁寧に導いた
グラフでの凸部分が特徴的に見えるので、
この座標を求めるところから始めてみましょう。
この座標は、第一象限における
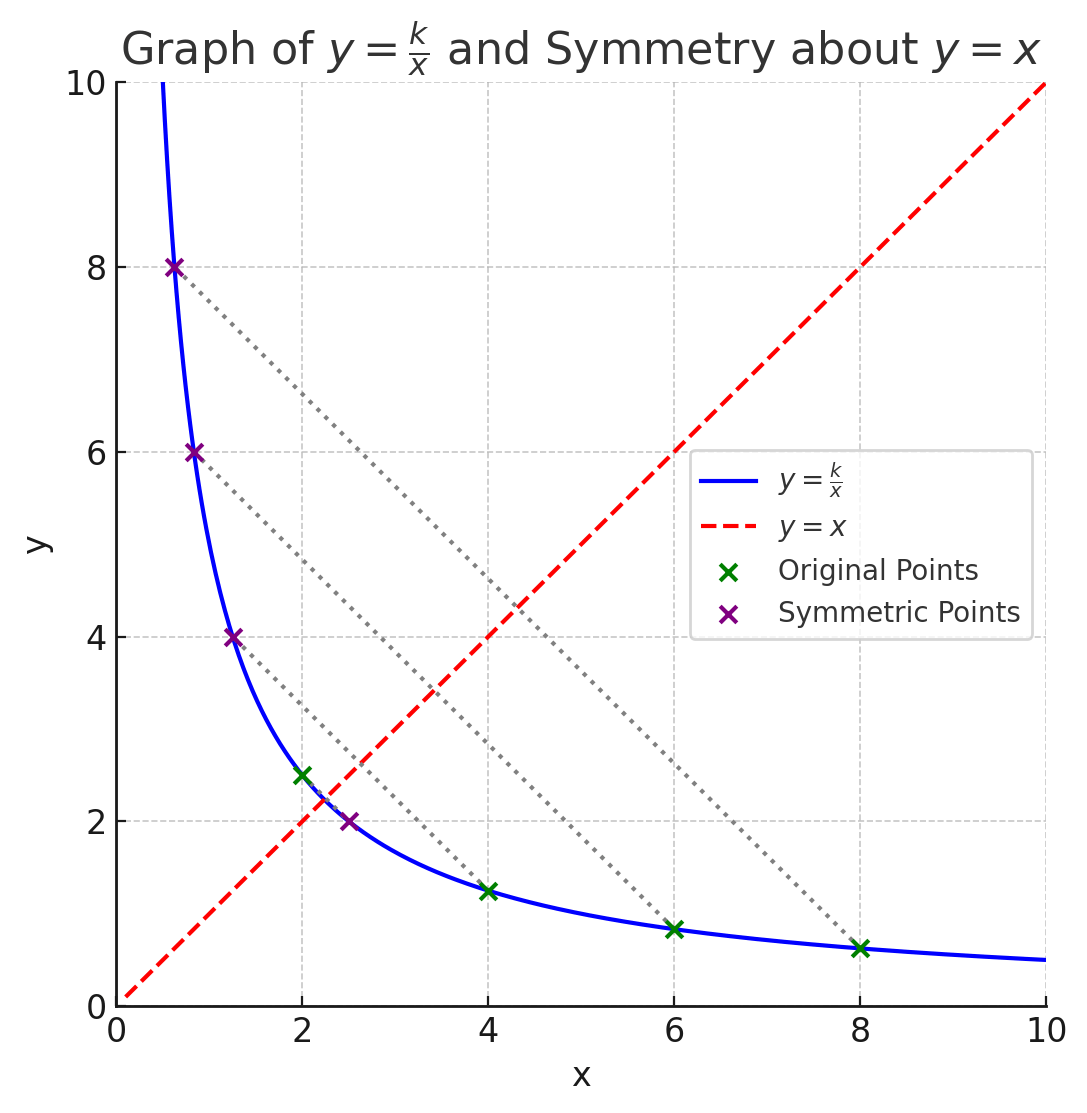
一応証明しておくと、
下グラフのように、
座標
座標
つまり、
において、
が成り立つかどうかを確認します。
難なく
となるため、
関数
では、そのまま、凸部分の座標を求めてしまいます。
今後この座標を流動性
では、
において、流動性
となります。
したがって、流動性
です。
以下のように表せます。

では、この
この点に注目して、一旦UniswapV2の実装から離れて、
あなたは、再び、ボトルの管理者となることにしましょう。
再び、MTK、USDCの入ったボトルを管理することになります。
今回のあなたはこれまでとは一味違い、
ある程度ボトルの特性を分析して、準備を行うことにしました。
のルールをベースにすると、あなたは管理者としては、最低限のスタート位置にいます。
では、このルールは、あくまでの最低限ボトルが空っぽにならないというものでした。
あなたは、考えます。
「これ、
試しに
とすると、過去にこのようなグラフを見ましたよね?
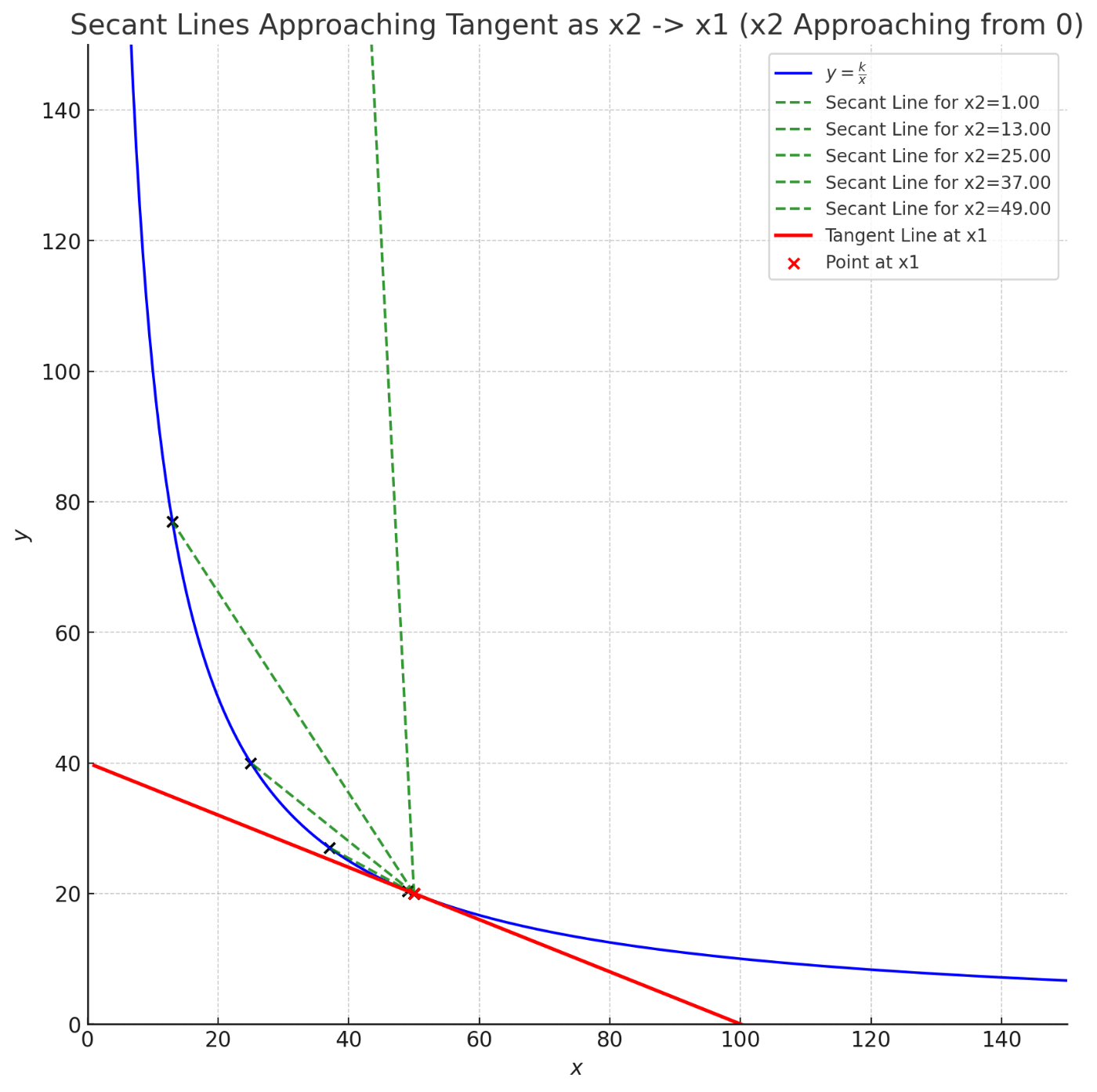
あなたは気がつきます。
「
ということで試してみました。
同じ価格、同じ取得難易度のところからスタートしたとき、

みてわかる通り、
つまり、
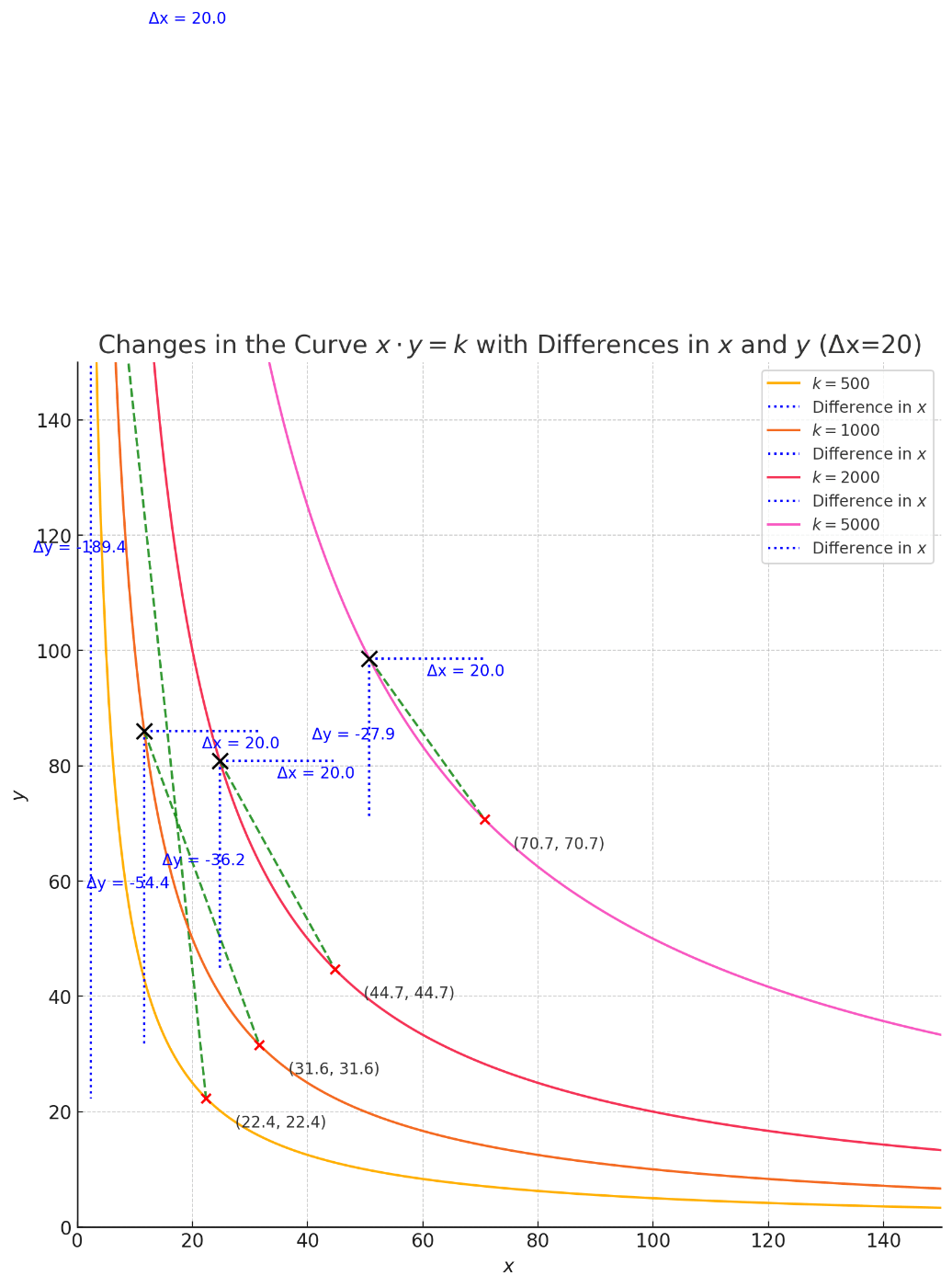
さらに一般化してグラフにしたものが以下です。
難易度の変化が緩やかになっていることが下段グラフをみるとわかります。
あなたは考えます。
「
最初に入れる
ここで、より、
そもそも
これが大きいほど、大幅な価格の影響を受けない、安定度の高い環境になるというわけです。
これは直感と合致している気がします。
たくさんの量を扱っているほど、何かに対する影響からは安定しそうですよね。
この量的な何かである
掛け算は少し難易度高いので、
すでに言及しましたが、
したがって、全てのユーザが預けたその流動性(とスワップによる手数料を合わせたもの)が
このコントラクトアドレスの所持分であるといえます。
流動性の合計は、UniswapV2Pairコントラクトの残高であり、リザーブでもあります。
したがって、
これは、ボトルの中の総量を端的に表しているとイメージしやすくないでしょうか?
話を単純に平均(算術平均)してみると、
このようになります。
これはボトルの中の基礎トークンに何も重み付けをしないで、
数量だけ計算した場合の平均した1基礎トークンあたりの量を表しているといえます。
この延長線上で、
掛け算の平均(幾何平均)は、かけた数だけn乗根を取ればいいので、
平均した1基礎トークンあたりの量は、
と表せます。
※ただし、一般的に幾何平均は、変化率の平均と捉えられると多いますが、
掛け算をベースとした場合の1つあたりの平均値と今回は捉えてみます。
さて、このイメージを幾何的に捉えると以下のようになります。

どうやら、凸部の座標と原点からなる正方形の面積のことのようです。
一度まとめますと、
幾何的には、
このイメージをもとに、
いよいよ、初めてUniswapV2の機能の1つに触れることとなります。
締め:中編に続く
圧倒的に紙面が紙面が足りませんでした...
中編に続きます...
現在準備中。
三部作通しての参考文献
下記ページの最下部をご確認ください。
Discussion