💨

Wavelet Scatteringを用いた深層生成モデルとその実験結果の解説【忘備録】

2023/05/31に公開

ディープラーニング

はじめに

VAE（Variational Auto-Encoder）はエンコーダーを有する（次元圧縮を伴う）深層生成モデルで、様々な研究がなされ広く用いられていますが、他のニューラルネットワークと同様にブラックボックスでモデルの解釈が困難です。また、エンコーダーとデコーダーともに多数のパラメータを学習する必要があります。Angles & Mallat (2018)で提案された深層生成モデルは、エンコーダーがWaveletを用いた特徴抽出法（Wavelet Scattering）とPCAで構成されており、解釈性が高く、また、エンコーダーは学習パラメータを含んでおらず学習が不要です。この解釈性が高く学習不要なエンコーダーで具体的にどのような表現が得られるのか興味が湧いたので、この深層生成モデルを実装して試してみることにしました^[1]。

本記事では、この深層生成モデルの概要と実験結果をゆるく説明したいと思います（実験結果だけ見たい方はこちらへとんでください）。

モデル

深層生成モデルの全体像を以下の図に示しました。
図 1.　深層生成モデル（Angles & Mallat, 2018）の全体像のイメージ
このモデルはエンコーダーとデコーダーで構成されます。Wavelet ScatteringとPCAからなるエンコーダーで画像を低次元の潜在変数ベクトルに変換し、それを畳み込み層を用いたデコーダー(convolutional generator)で画像に復元します。以下では、エンコーダーについて解説した後、デコーダーについて解説します。

エンコーダー

エンコーダーでは、まず、画像にWavelet Scatteringを適用し、Scattering係数という特徴量を得ます。そのScattering係数をPCAで次元圧縮かつ白色化して低次元の潜在変数ベクトルを得ます。以下では、Wavelet Scatteringの概要を説明した後、Scattering係数のPCAについて少しだけ補足説明します。

Wavelet Scattering概要

Wavelet Scatteringは複素Wavelet畳み込みを用いた特徴抽出法で、畳み込みネットワークに似た処理を行います。畳み込みネットワークは、学習パラメータからなるフィルタでの畳み込み、プーリング、活性化関数(ReLU)で構成されるのに対して、Wavelet ScatteringはWaveletフィルタ、ローパスフィルタでの畳み込み、複素絶対値変換で構成されます。畳み込みネットワークよりシンプルな処理で解釈性が高く、学習パラメータを含まないため学習が不要です。

まず、基本設定です。Wavelet Scatteringのスケールを $2^J$ として、スケール $2^J$ の空間情報を集約するようにします。畳み込みに使うWaveletは、２次元のWavelet Scatteringでもっともよく使われる２次元Morlet Waveletとします。Waveletフィルタ $\psi_{j,q}$ は次式のように、Mother Wavelet $\psi$ を $2^j$ だけスケールし、角度 $\pi q/Q$ だけ回転させて構成します。

\psi_{j,q} (u) = 2^{-2j} \psi (2^{-j} R_{-q} u), 　j=1,\ldots,J, \ q = 0,\ldots,Q-1.

ここで、

R_{-q}

は角度

-q

の回転行列です。ローパスフィルタは、スケール

2^J

のガウシアンローパスフィルタ

\phi_J(u) = 2^{-2j} \phi (2^{-j} u)

を用います。Wavelet Scatteringは、このWaveletフィルタとローパスフィルタを用いて、次の、０次、１次、２次のScattering係数を画像の特徴量として算出します。

０次Scattering係数：
画像（１チャンネル） $x$ とローパスフィルタ $\phi_J(u)$ の畳み込みを行います。その畳み込みの値を $2^J$ の間隔でサンプリングして得られる値

$x \star \phi_J(2^J u)$ が０次Scattering係数です。このローパスフィルタでの畳み込みにより、スケール $2^J$ の範囲で画像を平均操作で集約しずれや歪みに対してロバストな表現を得ることができたのですが、当然多くの情報（低周波帯域以外の成分）を損失しています。次の１次のScattering係数では、Waveletフィルタで畳み込みを行い、ここでロスした情報を抽出します。
１次Scattering係数：
画像 $x$ をWaveletフィルタ $\psi_{j,q}$ で畳み込んだ後、複素絶対値に変換します。これをローパスフィルタ $\phi_J(u)$ で再度畳み込んで $2^J$ の間隔でサンプリングします。これによって、次の1次Scattering係数を得ます。
$\left \{ | x \star \psi_{j,q}| \star \phi_J(2^J u) \right \}_{1\leq j\leq J,\ 0\leq q<Q }.$ この1次Scattering係数では、０次Scattering係数で損失した情報（低周波帯域以外の成分）をスケール（周波数帯域）および角度ごとにフィルタリングし、複素絶対値変換して集約します。ただし、ここでもWavelet畳み込みの絶対値をローパスフィルタで集約する際に、低周波数帯域以外で情報が損なわれています。そこで、次の2次のScatteringでは、Wavelet畳み込みの絶対値をさらにWaveletフィルタで畳み込みます。
2次Scattering係数
まず、1次Scattering係数の計算をローパスフィルタをかける前のところまで実行します。すなわち、画像 $x$ とWaveletフィルタ $\psi_{j,q}$ の畳み込みを複素絶対値に変換します。これをWaveletフィルタ $\psi_{j^{\prime},q^{\prime}(j^{\prime}>j)}$ で畳み込んで、複素絶対値に変換します。０と１次のScatteringと同様に、これをローパスフィルタ $\phi_J(u)$ で畳み込んで $2^J$ の間隔でサンプリングすると次式の２次Scattering係数が得られます。

$\left \{ || x \star \psi_{j,q}|\star \psi_{j^{\prime},q^{\prime}}| \star \phi_J(2^J u) \right \}_{1\leq j < j^{\prime} \leq J,\ 0\leq q,q^{\prime} <Q}.$ ２次Scatteringのローパスフィルタをかける前の値にさらにWaveletフィルタでの畳み込みと絶対値変換を繰り返し、3次、4次と次数を増やしていくことも考えられます。しかしながら、種々のタスクにおいて、3次以降のScattering係数は有意義な情報を含んでいないことが確認されており、2次までのScattering係数が用いられています。

Scattering係数のPCA

Wavelet Scatteringで得た0,1,2次のScattering係数をPCAで次元圧縮かつ白色化します。この結果得られた低次元の潜在変数ベクトルが画像のエンコード結果となります。

論文では、この潜在変数ベクトルに関して以下のようなことを主張しています。「Scattering係数は、変換したデータのローパスフィルタによる平均であり、Wavelet Scatteringのスケールが十分大きいとき、中心極限定理の効果でその分布が正規分布に近づく」。もしこれが成り立つ場合、Scattering係数をPCAで白色化した潜在変数ベクトルは近似的に多変量標準正規分布（相関０，分散１，平均０）に従うので、潜在変数ベクトルを用いてデコーダーを学習することで、多変量標準正規分布の確率標本から画像を生成するデコーダーを得ることができると、著者達は考えたのだと思われます。

デコーダー

上記のエンコーダーに画像を入力し、得られた潜在変数ベクトルをデコーダーで元の画像に復元します。デコーダーとして、DCGANのGeneratorと同じようなアーキテクチャのConvolutional Generator（畳込みを用いたGenerator）を用います。

Convolutional Generator

Convolutional Generatorのアーキテクチャを把握しやすいように、図2にConvolutional Generatorの各ネットワーク層の出力テンソルのイメージを図示しました（ここでは、線形変換から活性化関数による非線形変換までをひとまとめにしてネットワーク層と呼ぶことにします）。
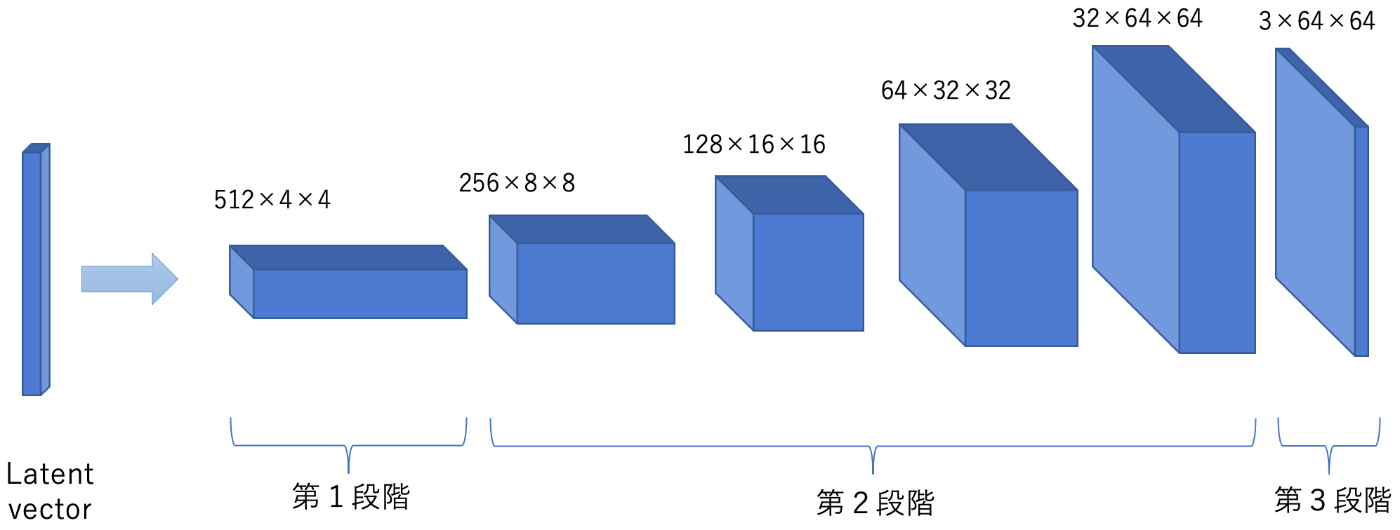図 2.　Convolutional Generatorの各ネットワーク層の出力テンソルのイメージ。立方体の上の数字はテンソルのサイズを表しています。画像サイズは64x64のカラー画像（チャンネル数３）です。
Convolutional Generatorのアーキテクチャは３段階で構成されます。以下、第１段階のネットワーク層から順に（図2を参考にしながら）説明していきます。

第１段階：
潜在変数ベクトルを以下のネットワーク層で変換します。
全結合層 → 3次元テンソル（C×H×W）に変換 → バッチ正規化 → Relu関数
この3次元テンソルのサイズC×H×Wは、C>>H,Wとします。例えば、図２ではC=512,H=W=4で、第１段階と記入した半カッコで囲った立方体で表しています。このテンソルをサイズがH×Wでチャンネル数がCの画像と考え、次の段階で、チャンネル数を圧縮しながら画像のサイズが元の画像のサイズになるまでアップサンプリングします。
第２段階：
３次元の出力テンソルに対して以下のネットワーク層を画像のサイズが元の画像のサイズになるまで繰り返し実行します。
bilinear upsampling →　畳み込み層 → バッチ正規化 → Relu関数
bilinear upsamplingでは、入力テンソルの画像サイズをバイリニア補間を使って２倍に拡大します。次の畳み込み層は、strideが１、paddingがサイズ（kernel幅(odd)-1)/2であり、入力と出力の画像サイズが同じ値になります。　また、出力テンソルのチャンネル数は入力のチャンネル数の半分になります。このネットワーク層の繰り返し実行により、画像サイズを２倍に拡大しながらチャンネル数を半分に圧縮していきます。図２では、これら出力テンソルを第２段階と記した半カッコで囲った４つの立方体で表しています。
第３段階：
元の画像と同じ画像サイズになったテンソルを以下のネットワーク層で変換し、復元画像を出力します。
畳み込み層 → バッチ正規化 → tanh関数
この畳み込み層は、入力と出力の画像サイズが同じで、出力のチャンネル数が元画像のチャンネル数（カラーの場合３，モノクロの場合１）になります。tanh関数による変換を経て、最終的に値[-1,1]の画像を出力します。図２では、この出力画像をカラー画像として最も右の立方体で表しています。

デーコーダーの学習

画像をエンコーダー（Wavelet ScatteringとPCA）で潜在変数ベクトルに変換し、それをデコーダー（Convolutional Generator）に入力し復元画像を生成します。この復元画像と元画像の差のL1ノルムの平均を損失関数として、損失関数が最小となるようなConvolutional GeneratorのパラメータをAdamで探索します。

実験結果

CelebAの顔画像データセットを使って、論文と同じ内容の以下の実験を行いました。

画像の復元
正規乱数を使った画像生成
画像のモーフィング

CelebAの画像をトリミング、縮小してサイズ64×64の画像に変換して入力画像としました。Wavelet Scatteringのスケールは $2^3=8$ とし、得られたScattering係数をPCAで１２８次元まで圧縮して潜在変数ベクトルを生成します。その潜在変数ベクトルをConvolutional Generatorで以下のように変換していきます。第１段階目のネットワーク層では、512×4×4のテンソルに変換し、第２段階目の４つのネットワーク層でそれをアップサンプリングして32×64×64のテンソルに変換します。最後に第３段階目のネットワーク層で、値域[-1,1]でサイズ3×64×64の画像に変換します。ここで、畳み込み層のカーネルのサイズは5×5としました。

このConvolutional Generatorに含まれる5,404,966個のパラメータを、65,536枚の画像データで学習しました（論文の学習データと同じ枚数です）。バッチサイズは64、エポック数は100としました（学習しながら計算したヴァリデーションデータの復元誤差からモデルを学習しすぎでないことは確認しました）。

学習したGeneratorを使って、Wavelet ScatteringとPCAでエンコードした画像を復元しました。学習データの復元結果を図3に、テストデータの復元結果を図4に示しました。ともに、上段に元の画像、下段に復元画像を表示しています。どちらの場合も復元画像はVAEの結果のようにある程度ぼやけてます。

図 3. 学習データの復元結果

図 4. テストデータの復元結果

128次元の標準正規分布に従う乱数をConvolutional Generatorに入力して画像を生成しました(図5)。顔の輪郭の内側に関しては、人の顔として自然な画像はあるのですが、極端にぼやけていたり歪んでいるものの方が多いです。顔の輪郭の外側（髪の毛と背景）に関しては、極端にぼやけて不自然なものがほとんどです。（論文でも同様に、まともな顔画像をほとんど生成できていないので再現に失敗したわけではありません。）

図 5. 標準正規乱数から生成した画像

最後にモーフィングを行いました。まず、２枚の画像をWavelet ScatteringとPCAでエンコードし、２つの潜在変数ベクトル $z$ , $z'$ を生成します。この潜在変数ベクトル間を線でつないで $z$ から $z'$ へ少しずつ一定間隔で移動させながらConvolutional Generatorに入力して画像を生成しました。すなわち、 $z_{\alpha}=(1- \alpha)z + \alpha z'$ として、 $\alpha$ を０から１まで一定のステップ幅で増加させながら、 $z_{\alpha}$ をConvolutional Generatorに入力して画像を生成しました。学習データから選択した画像ペアとテストデータから選択した画像ペアのモーフィング結果をそれぞれ、図6と図7に示しました。どちらも図の左右両端に選択した画像の復元結果を表示し、その間に $z_{\alpha}$ の $\alpha$ の値を増加させながら生成した画像を表示しました。左端の画像から右端の画像へ連続的に変化する画像を生成できています。

図 6. 学習データのモーフィング結果

図 7. テストデータのモーフィング結果

以上、画像のサイズは異なるのですが、論文の実験結果と定性的に同じような結果を得ることができました。

コード

実験で深層生成モデルの学習と検証に使用したコードは近いうちに公開する予定です。

このコードは、学習したモデル（のパラメータ）と学習に用いたOptimizer（のパラメータ）をまとめて保存するようになっており、保存した学習済みモデルを引き続き学習できるコードになっています。これにより、学習が途中で中断した場合でも、保存したところから残りの分を学習することができます。

おわりに

Angles & Mallat (2018)によって提案されたWavelet Scatteringを用いた深層生成モデルとその実験結果を解説しました。実験では、CelebAの顔画像データを使って、画像の復元、正規乱数を使った画像生成、画像のモーフィングを行いました。論文の結果と同様に、画像の復元とモーフィングはVAEと同程度の結果が得られたのですが、正規乱数を使って生成した画像は人の顔として不自然なものが多く、VAEより大きく劣る結果となりました。画像の生成能力は不十分で改善の必要があると思います。

References

Angles & Mallat (2018) generative networks as inverse problems with scattering transforms, ICLR.
Liu Ziwei, Luo Ping, Wang Xiaogang & Tang Xiaoou (2015) Deep Learning Face Attributes in the Wild, ICCV, CelabA Dataset.

脚注

論文の著者がモデルのソースコードを公開しているのですが、以下のような理由で、このソースコードを使わず、全て自分で実装しました。
　1. PCAによる次元圧縮、白色化のコードが抜けている。
　2. 扱いづらい（コードを直接書き換えないとモデルのネットワークアーキテクチャを調整できない等）。
　3. モデルを改良することを考えており、自分で実装することでモデルをしっかり把握しておきたい。 ↩︎