🐙

B-tree について

2022/04/10に公開

file

btree

tech

本記事について

B-tree とはデータを保存するためのデータ構造の 1 つでデータベースにおいて最もポピュラーなデータ構造である．本記事を読むことでなぜ B-tree がここまでポピュラーであるか理解できるだろう．

データの保存形式

データはファイル形式でメモリやディスクに保存される．具体的にどのように保存されるか見ていこう．
データを保存するためのファイルの種類はいくつかあるが，ここではヒープファイルを想定する．ヒープファイルとはページという大きさにファイルを分割し，順序関係なくデータをページに書き込むことができるファイルである．またファイルはデータファイルとインデックスファイルに分けられ．本記事では B-tree はインデックスファイルに用いられるものとする．(データファイルに用いられることもある．) インデックスについての説明は省略するが，要するにインデックスからデータを参照することができる．

ファイルの構成

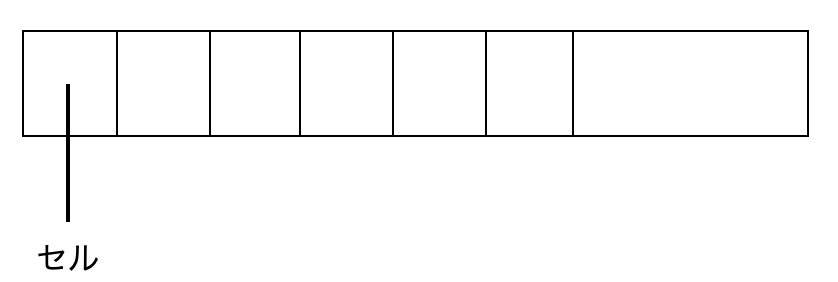
データファイルのページ構成

ファイルのヘッダ，トレーラには保持できるフィールド数，順序，型などのページのデコードに必要な情報が格納される．
ページはセルという大きさに分割され各セルにデータが格納される．
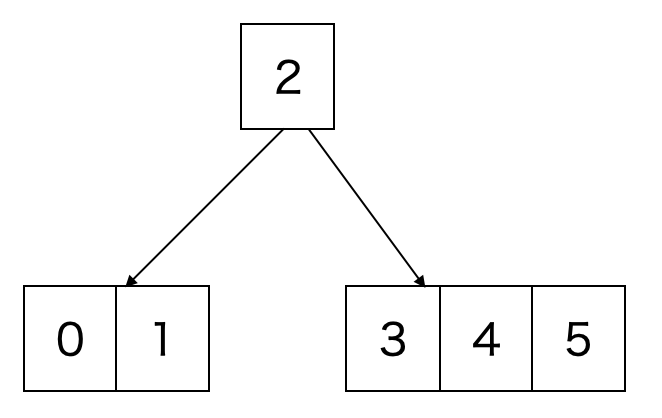
インデックスファイルに用いられる B-tree の構造は以下のようなものである．

B-tree のページ構成
ここで p は子ページへのポインタ，k は key， $\alpha$ は value である．よってレコード (行データ) を key と value に分けることで B-tree を用いることが可能になる．以下では具体的に B-tree の構造についてまとめる．

余談

基本的にはプライマリーキーとそれ以外というように key と value に分ける．プライマリーキーは一意である担保がされているのでインデックスとしてふさわしい．しかしインデックスとしての効果を発揮するのはプライマリーキーを条件として (WHERE 句に入れて) レコードを検索する場合のみである．実際の場合プライマリーキーで検索することはほとんどないので，検索の条件としたいカラムにインデックスを貼るのが妥当である．これをセカンダリインデックスと呼ぶ．この場合のデータ保持や検索の方法については別途記事で説明するとしよう．

B-tree における key の挿入

まず B-tree がどのように作られるのか確認する．key の挿入は以下のように行われる．(子ページへのポインタや value は以下の図で省略している)

まず key が並び替えられながら，格納される．

次にページが満杯になったらページが分割され，真ん中の要素が親ノードに入りその左と右のノードが子ノードとなる．(ここでノードとページは同じ意味)

そして再びリーフノード (最下層のノード) に key が格納される．

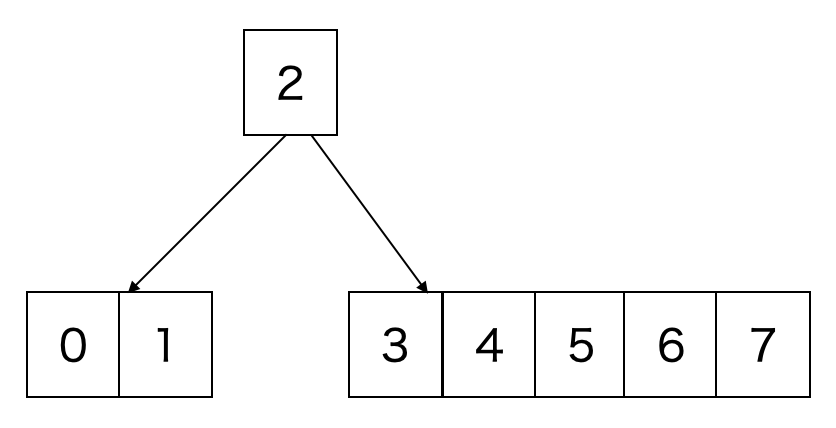
同様にページが満杯になったら分割される．

B-tree における key の削除

次に key がどのように削除されるかを確認する．

削除したい要素がリーフノードにあるケース

このケースでは要素を検索して単純に削除をすればよい．
まずルートノードを検索する．各ノードは要素がソートされているので二分探索できる．もしそのノードに目的の要素がなければ，子ノードを検索する．ノードごとに要素の大きさの順序は保たれているので検索すべき子ノードは一意に決まる．この操作を繰り返し行えば良い．

削除したい要素がリーフノードにないケース

このケースでは単純にその要素を削除するだけだと B-tree の構造が崩れてしまうので工夫が必要である．
以下のように削除する要素を見つけたら，その位置を保持しておく．

その要素の前後の子ノードのうち要素数が多いノードから要素を削除する要素の位置に移動させることで B-tree の構造は保たれる．

B-tree のメリット

B-tree はこのような構造になっているのでいくつかのメリットがある．
まず二分木との違いから見ていく．通常の二分木では要素が格納される順番によっては木が偏ってしまい検索の効率が悪くなってしまうが，B-tree の場合はこのような挿入方法にすることで偏ることがなくなっている．また 1 つのノードに入れることができる要素が複数なので木の高さも高くなりにくいので効率が良い．
ディスクとの関係からも B-tree のメリットを語ることができる．最初に述べたようにファイルはディスクに保存される．ディスクへのアクセスのブロックという単位で行われる．B-tree では 1 ノード (ページ) がブロックに対応するので，1 回のディスクアクセスで 1 ページ取得でき無駄がないようにできている．

このように計算効率の面で B-tree を用いることは有用なのである．

参考文献

[1] Alex Petrov 著，小林隆浩監訳，成田昇司訳，詳説データベース
[2] Bayer, R., and E. M. McCreight. 1972. “Organization and maintenance of
large ordered indices.” Acta Informatica 1, no. 3 (September): 173 - 189. https://doi.org/10.1007/BF00288683.