応用情報試験 令和6年 午前I 問75
対象読者
以下の応用情報試験 令和6年 午前I 問75の問題の解き方が分からない人向け。

何を学べば解けるのか?
上記の問題は線形計画法や数理計画法と呼ばれる最適化手法に関する問題です。
ご興味のある方は、数理計画法による最適化を見てみてください。
何の役に立つのか?
問題の内容から察している方も多いと思います。
実際、工場で製品を作るとき、無駄な部品は仕入れたくないですし、利益は最大化したいですよね。
これをどんぶり勘定や勘ではなく、理論に基づいて仕入れを決定したいのが経営者です。
そして、その経営者の求める解を手計算ではなく、プログラムを使って一瞬で解くのがイケているITエンジニアです。
つまり、解けるようになると会社が儲かるということです。
問題を整理しよう
まず、製品Xと製品Yと言われてもイメージしにくいですし、部品Aと部品Bと言われてもイメージしにくいので具体的な製品と部品で考えてみましょう。
製品X:ポータブルスピーカー
製品Y:コンパクトラジオ
部品A:バッテリー
部品B:スピーカー
としましょう。
問題文では、まず、ポータブルスピーカーを作って売ると1万円儲かります、コンパクトラジオを作って売っても、1万円儲かりますと言っています(下図)。

これだけ読むと「どっちを作っても同じじゃないか?」と思いますよね。
でも、次にポータブルスピーカーを作るにはバッテリーが3個とスピーカーが1個必要だ、と言っています。また、コンパクトラジオを作るにはバッテリーが2個、スピーカーが2個必要だと言っています。つまり、ポータブルスピーカーとコンパクトラジオを作って売るとどちらも1万円儲かりますが、使う部品の数が違うと言っています(下図)。

さらに、バッテリーとスピーカーの数には限りがあります。倉庫にはバッテリーが120個、スピーカーが60個しかありません。と言っています(下図)。

まだ何が問われているのかわかりにくいと思いますので、試しにポータブルスピーカーだけを作った場合を考えてみましょう。
[ポータブルスピーカーだけを作ると考えた場合]
ポータブルスピーカーを作るにはバッテリーが3個とスピーカーが1個必要です。
ポータブルスピーカーだけを作ると考えた場合、120÷3=40個でポータブルスピーカーは40個作れます。そして、スピーカーが20個余ります(下図)。

スピーカーが20個も余るなんて勿体ないなって思いますね。
では、コンパクトラジオを作ったとしたらどうなるでしょう?
[コンパクトラジオだけを作った場合]
コンパクトラジオを作るには、バッテリーが2個、スピーカーも2個必要です。
スピーカーは60個なので、60÷2=30でコンパクトラジオが30個作れてバッテリーが60個余ります。

バッテリーが60個も余るのも勿体ないですね。
バッテリーとスピーカーを余らせることなくポータブルスピーカーとコンパクトラジオを作ることが出来たらもっと儲かりそうです。
では、ポータブルスピーカーとコンパクトラジオをそれぞれ何個ずつ作れば、儲かるでしょうか?ということが問われていることになります。
解き方
まず、目的です。目的は利益を最大化することです。ポータブルスピーカーの台数をx台作ると10,000円儲かります。また、コンパクトラジオをy台作っても10,000円儲かります。そのときの利益をzとすることを式で表すと次のとおりになります。これを目的関数と呼びます。
次にバッテリーは120個しかないことを式に表すと、次のようになります。
また、スピーカーは60個しかないことを式に表すと、次のようになります。
上記二つの式は制約条件と呼びます。
それぞれの制約条件を中学でならった、
の形に直してみましょう。
は
となります。
グラフで表すと下図のようになります。
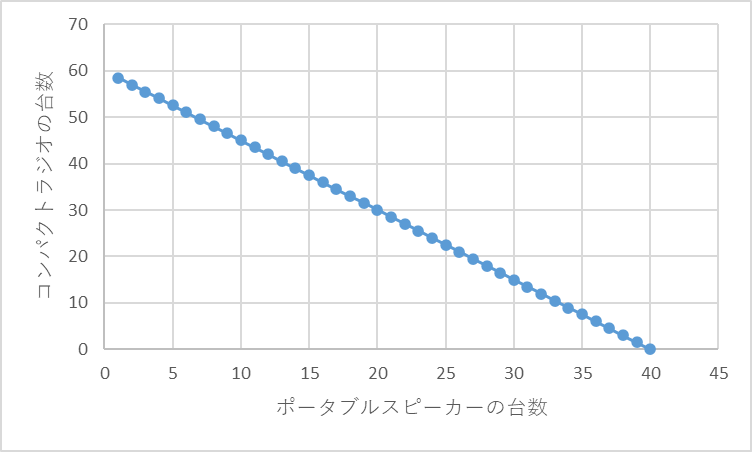
このグラフは、バッテリーが120個しか使えないという条件でポータブルスピーカーとコンパクトラジオを作れる台数の関係を示したグラフになります。
また、
は、
となります。
グラフで表すと下図のようになります。
この二つの関数をグラフで表すと下図となります。

このグラフは、スピーカーが60個しか使えないという条件でポータブルスピーカーとコンパクトラジオを作れる台数の関係を示したグラフになります。
そして、この二つのグラフを重ねると下図のグラフが得られます。

このうち、バッテリーの制約とスピーカーの制約を満たす部分は下図の灰色部分になります。

バッテリーの制約とスピーカーの制約の両方を満たしつつ、目的関数が最大となる場所を探すのが次の目標です。
目的関数は、次の式でした。
これを1次式に変形すると次のようになります。
目的はzが最大となるxとyの組み合わせを考えることです。ということは、切片が最大となる場所をグラフから探せばよいということになります。
目的関数をグラフにプロットしたとします(赤色)。zの値を変更するということは目的関数を平行移動させることと同じことです。

一番上の赤色の目的関数は、制約条件(灰色)を通過していませんので、制約条件を全く満たしていません。
一番下の赤色の目的関数は、制約条件(灰色)を通過していますが、もっとzを大きくしても制約条件を満たしそうです。
真ん中の赤色の目的関数は、バッテリーの制約とスピーカーの制約のグラフの交点を通過しています。
つまり、交点がギリギリ制約条件を満たしつつ、目的関数を最大化できているグラフと言えます。
交点は、
からx=30となり、y=15となります。
問われていたのは「利益は最大何万円になるか?」でした。
そして目的関数は、以下のとおりでした。
得られたxとyの値を目的関数に当てはめると、
となります。
よって、答えはウの45万円になります。
Discussion