Transformerの上位互換となりうるRetentive Network(RetNet)が話題だったので、論文を読んでまとめてみました
論文はこちら
https://arxiv.org/abs/2307.08621
(2023年7月)
概要
ざっくりいうとTransformerとRNN等の回帰型ニューラルネットワークの良いとこ取りをしたもので、今までのアーキテクチャだと両立が難しかった以下の3軸を同時に満たすことができます
- 学習時の並列実行
- 低コストの推論
- 性能の高さ
具体的には、TransformerのAttention層をRetention層というものに入れ替えた構造で、Retention層は2つの異なる形で表現されます
2つの異なる形で表現されるとはどういうことか…
まずRetention層を以下の式で表します
\bm{X}という入力に対してOutputという出力をする関数です
このRetention関数を具体的な数式に展開すると、以下の2つの異なる数式になります
(どちらの数式でも入力\bm{X}に対して同じ出力Outputとなる)
- 並列表現
- 回帰表現
並列表現
並列表現では学習時に膨大なデータを並列に実行できます
数式にするとこの形
Retention(\bm{X})=(\bm{QK}^{T}\odot\bm{D})\bm{V}
nをデータの長さ、dを隠れ層の次元、\bm{X}\in\mathbb{R}^{n×d}として
\bm{Q}=(\bm{XW_Q})\odot\bm{\Theta}\in\mathbb{R}^{n×d} \\
\bm{K}=(\bm{XW_K})\odot\bar{\bm{\Theta}}\in\mathbb{R}^{n×d} \\
\bm{V}=\bm{XW_V}\in\mathbb{R}^{n} \\
\bm{D}=\begin{pmatrix}
1 & 0 & 0 & \dots & 0 \\
\gamma & 1 & 0 & \dots & 0 \\
\gamma^2 & \gamma & 1 & \dots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
\gamma^{n-1} & \gamma^{n-2} & \gamma^{n-3} & \dots & 1
\end{pmatrix}\in\mathbb{R}^{n×n}
上記のように\bm{Q,K,V}と\bm{D}を定義します
なお…
-
\bm{W_Q}\in\mathbb{R}^{d×d}、\bm{W_K}\in\mathbb{R}^{d×d}、\bm{W_V}\in\mathbb{R}^{d}は学習パラメータ
-
\odotはアダマール積(要素ごとの積)
-
\bm{\Theta}_n=e^{in\bm{\theta}}、\bm{\theta}\in\mathbb{R}^{d}
-
\bar{\bm{\Theta}}は\bm{\Theta}の複素共役
です
TransformerのAttention層が
Attention(\bm{X})=softmax(\frac{\bm{QK}^T}{\sqrt{d_k}})\bm{V}
なのでかなり似た形ですね
学習時の計算も同様に並列実行できます
なお、\bm{D}の行列はTransformerでいうマスクや相対位置表現にあたる役割を果たしています
回帰表現
回帰表現では推論時に少ない計算量で低コストに実行できます
数式にするとこちら
Retention(\bm{X})_n=\bm{Q}_n\bm{S}_n
\bm{S}_n=\gamma\bm{S}_{n-1}+\bm{K}^T_n\bm{V}_n\in\mathbb{R}^{d} \\
(\bm{S}_n=0)
\bm{Q,K,V}は並列表現と同じ行列です
この表現の場合、計算量がnの1乗のオーダーになります
Transformerはnの2乗オーダーなので、比較すると計算量がだいぶ少なくなります
2つの表現をまとめたのがこちらの画像
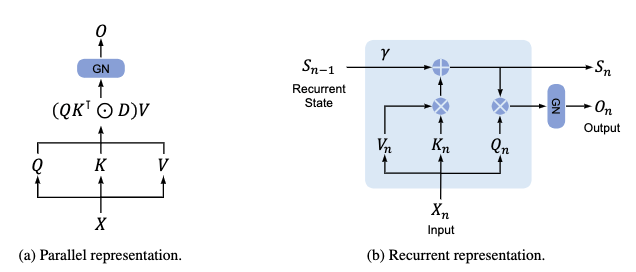
論文より転載
マルチスケールRetention
TransformerのマルチヘッドAttentionと同様に、複数ヘッドで並列に学習/推論が実行されます
dを1ヘッドの次元、d_{model}をモデル全体の隠れ層の次元、h=\frac{d_{model}}{d}をヘッドの数とし、\bm{W_G}\in\mathbb{R}^{d{model}×d{model}}、\bm{W_O}\in\mathbb{R}^{d{model}×d{model}}を学習パラメータ、\bm{\gamma}\in\mathbb{R}^hとしたときに
head_i=Retention(\bm{X},\gamma_i) \\
Y=GroupNorm_h(Concat(head_1,...,head_h)) \\
MultiScaleRetention(\bm{X})=(swish(\bm{X}\bm{W_G})\odot\bm{Y})\bm{W_O}
となります
swish()は活性化関数の1つでswish(x)=\frac{x}{1+e^{-x}}
\gamma_iは1-2^{-4-i}の値を設定します
結果
予想通りですが、学習時は既存のTransformerと近い性能に
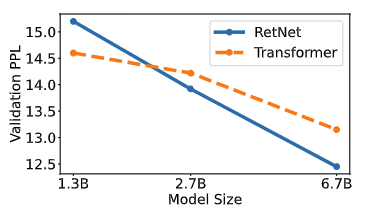
論文より転載
推論時は低コストで同等の結果を出しています
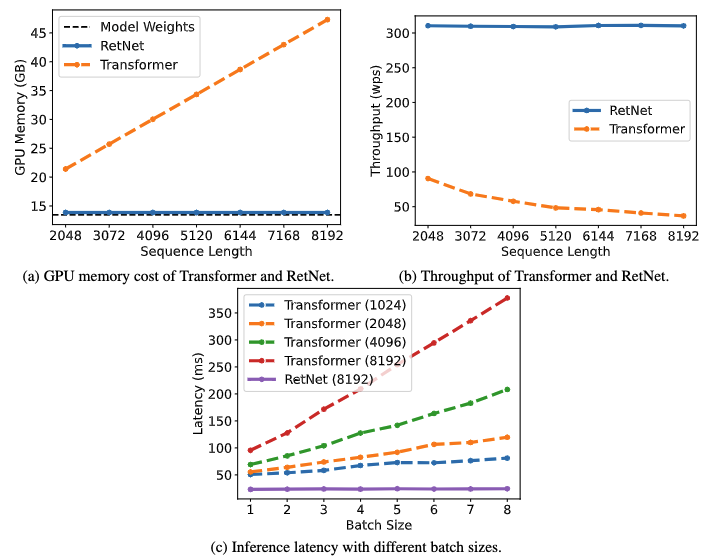
論文より転載
まとめ
今回は話題のRetNetの論文を読んでまとめてみました
要は数式をうまく使うことで推論時の計算量を大きく減少させるというもの
発想としてはLoRAと近いのかなと思いました
現状は大元のソースが公開されてるくらいですが、各プラットフォームで実装が進めば採用するメリットは大きいのかなと思いました



Discussion