🐈

ある範囲内の要素の値を切り替える区間クエリと区間和を実現する遅延セグメント木（AtCoder Library使用）

2022/02/05に公開

C++

競技プログラミング

AtCoder

tech

ある範囲内の要素の値を一方から他方へ変更する区間変更クエリと全体の総和をとるクエリを実現する遅延セグメント木を、AtCoder LibraryのLazySegmentTreeを用いて実装する方法について。

AtCoder Libraryの`LazySegmentTree`

どういう問題が解けるか

次のような問題が解ける。

問題

数列 $A = \{a_0, a_1, ..., a_{N-1}\}$ が与えられる。これと同じ数列、つまり $0\leq i < N$ の時 $a_i = b_i$ となる数列 $B = \{b_0, b_1, ..., b_{N-1}\}$ を用意する。以下の二つのクエリを処理してください。

$i = l, l+1, ..., r-1$ に対して、 $a_i = b_i$ ならば $a_i\leftarrow 0$ とし、 $a_i\neq b_i$ ならば $a_i\leftarrow b_i$ と変更する。
$i = l, l+1, ..., r-1$ に対して、 $\sum_{i=l}^{r-1}a_i$ を出力する。

制約: $1\leq N\leq2×10^5, |a_i| \leq 10^9$

解法

遅延セグメント木を用いる。
クエリ1の区間変更に関しては、それぞれの値の符号を反転させるようにする。
クエリ2の区間和は、セグメント木上の区間和をとってきた後に、元の配列の値の該当する区間の総和を足し、2で割ることで求められる。
元の配列の値の総和は累積和を用いて $O(1)$ で求められる。

クエリの回数を $Q$ とすると、各クエリは $O(log N)$ で処理できるので、全体の計算量は $O(QlogN)$ となる。

具体例

具体例は以下。seg[i]はセグメント木上の値、A[i]は元の配列の値を表す。

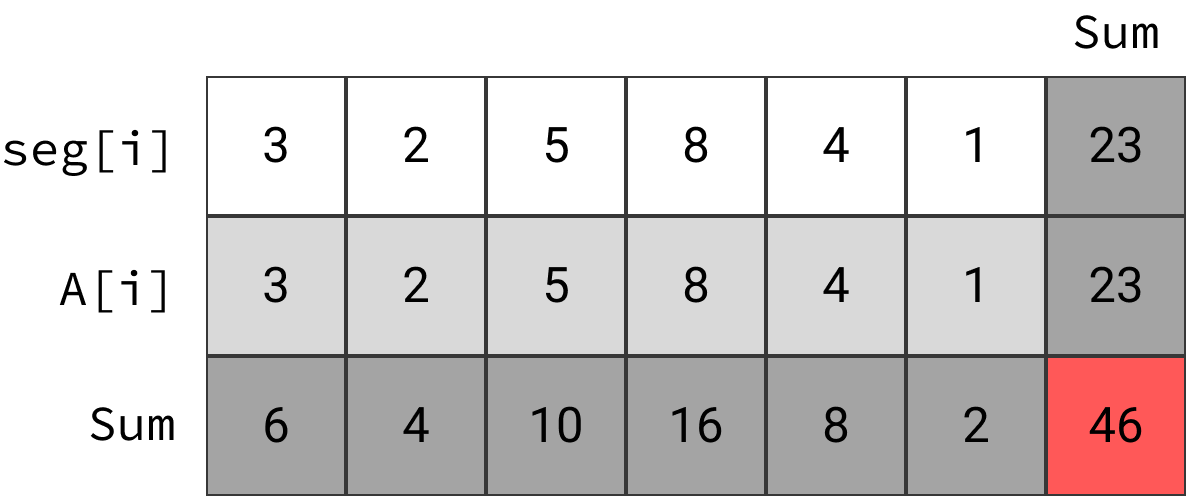
区間クエリに対して求める値は、列和の総和（もしくは行和の総和）である右下の赤いマスの値の半分である。各列の和を見ると、元の配列の値との和を取ることで、反転している要素の値はゼロになり、そのままの値は元の値の2倍になっていることがわかる。なのでこの列和の総和を2で割れば、反転していない要素の総和が求まる。

初期値

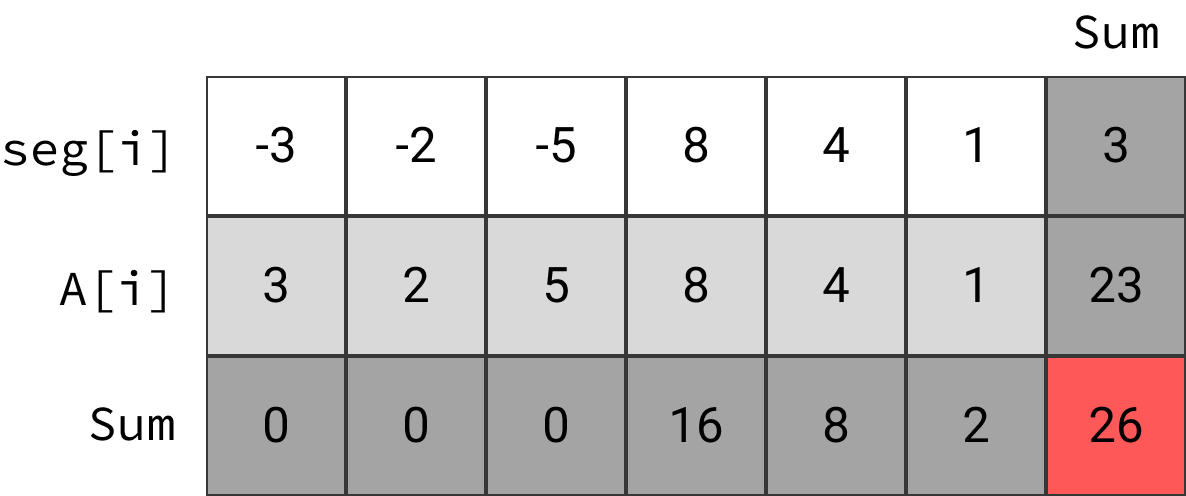
[0, 3) に対して反転を行う。

[2, 5) に対して反転を行う。

実装例

#include <bits/stdc++.h>
#include <atcoder/lazysegtree>
using namespace std;

namespace RangeToggleSumLazySegtree {
using S = long long;
using F = bool;
S op(S a, S b) { return a + b; }
S e() { return S(0); }
S mapping(F f, S x) { return f ? x : -x; }
F composition(F f, F g) { return f == g; }
F id() { return true; }

using _segtree = atcoder::lazy_segtree<S, op, e, F, mapping, composition, id>;

struct SegTree {
   private:
    vector<S> v, cum_sum;
    _segtree seg;

   public:
    SegTree(vector<S> v) : v(v) {
        seg = _segtree(v);

        cum_sum = {0};
        for (S &e : v) cum_sum.push_back(cum_sum.back() + e);
    }

    S prod(int l, int r) {
        return (cum_sum[r] - cum_sum[l] + seg.prod(l, r)) / 2;
    }

    S all_prod() { return prod(0, v.size()); }

    void apply(int l, int r) {
        seg.apply(l, r, false);
    }
};
}  // namespace RangeToggleSumLazySegtree

使用例

int main() {
    vector<RangeToggleSumLazySegtree::S> a = {3, 2, 5, 8, 4, 1};
    const int n = a.size();

    RangeToggleSumLazySegtree::SegTree seg(a);

    // 最初は全てその値
    cout << seg.all_prod() << endl;  // 23

    // [0, n) の値を切り替える
    seg.apply(0, n);  // -> a = {0, 0, 0, 0, 0, 0}

    cout << seg.prod(0, n) << endl;  // 0

    // [0, 3) の値を切り替える
    seg.apply(0, 3);  // -> a = {3, 2, 5, 0, 0, 0}

    cout << seg.all_prod() << endl;  // 10
    cout << seg.prod(2, n) << endl;  // 5

    // [1, 5) の値を切り替える
    seg.apply(1, 5);  // -> a = {3, 0, 0, 8, 4, 0}

    cout << seg.all_prod() << endl;  // 15
    cout << seg.prod(3, 5) << endl;  // 12

    return 0;
}

提出

PAST 第7回 N - モノクロデザイン/Monochrome Design　に対する提出。

もっといいやり方、ありそう？

あれば教えてください。