🐈

AHC031 7位解法

2024/04/10に公開

Rust

競技プログラミング

AtCoder

tech

はじめに

Atcoder Heurisitic Contest 031（AHC031）で7位でした！
初めての一桁順位なのでとても嬉しいです。
本記事では、私の解法について説明します。
他の上位勢と同じく、いわゆる「短冊解法」を採用しましたが、最適化対象の設定と状態の管理で工夫ができたと思うので、そこを重点的に説明します。

問題概要

高橋くんはイベントホールの管理をしている。このイベントホールは、パーティションを設置していくつかの長方形区画に区切ることが出来、各区画を別々の団体に貸し出している。
数日間の予約状況が与えられる。各予約ごとに希望する区画の面積が指定されており、割り当てた区画の面積が指定された面積を下回った場合、コストが発生する。また、区画の区切りを変更するためのパーティションの設置・撤去にも長さに応じたコストが発生する。出来るだけコストの総和が小さくなるようにイベントホールを運営して欲しい。

解法概要

私の解法は主に以下の2ステップからなります（いわゆる「短冊解法」です）。

列の構築
- 初日にイベントホール全体を区切るように、縦に仕切りを作成し、細長い列をいくつか作成する
予約配置の最適化
- 各列に割り当てる予約を仕切りの切り替えが少なくなるように最適化する

seed=5に対する解

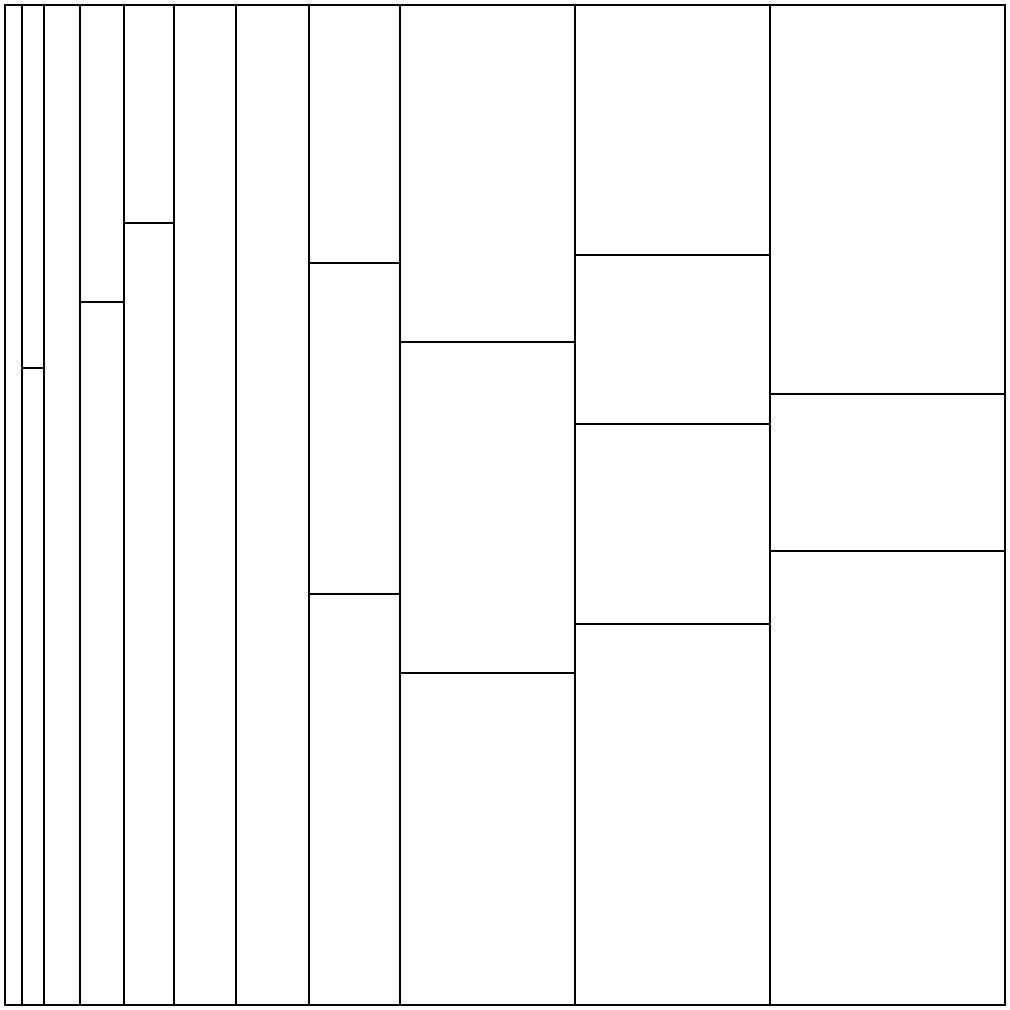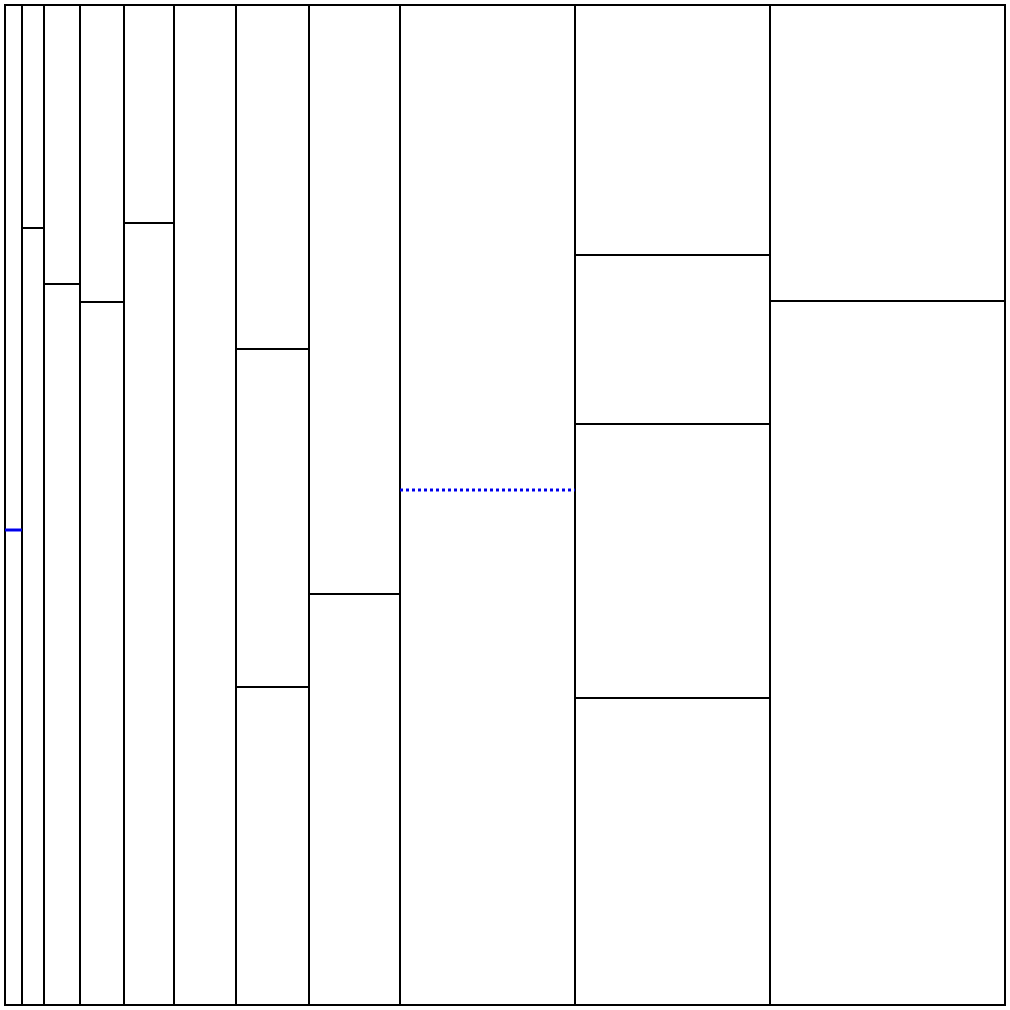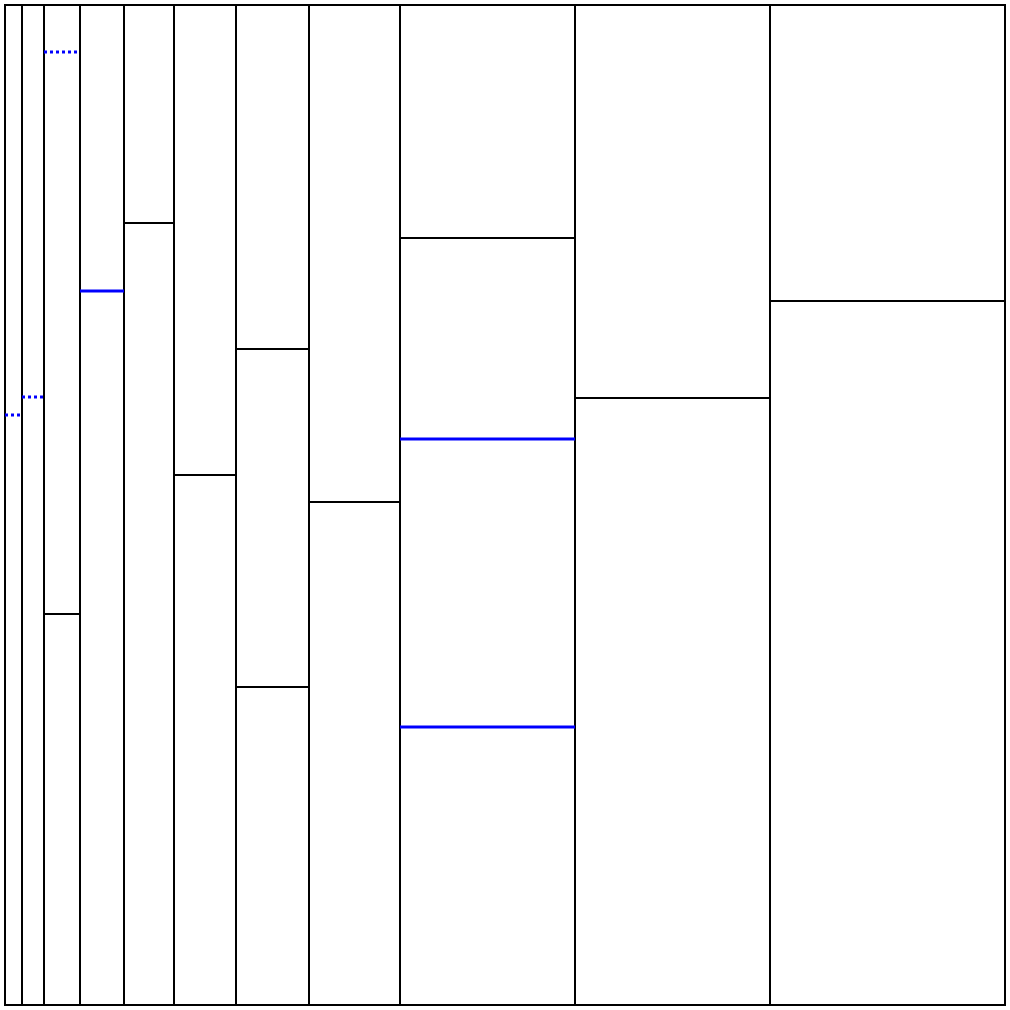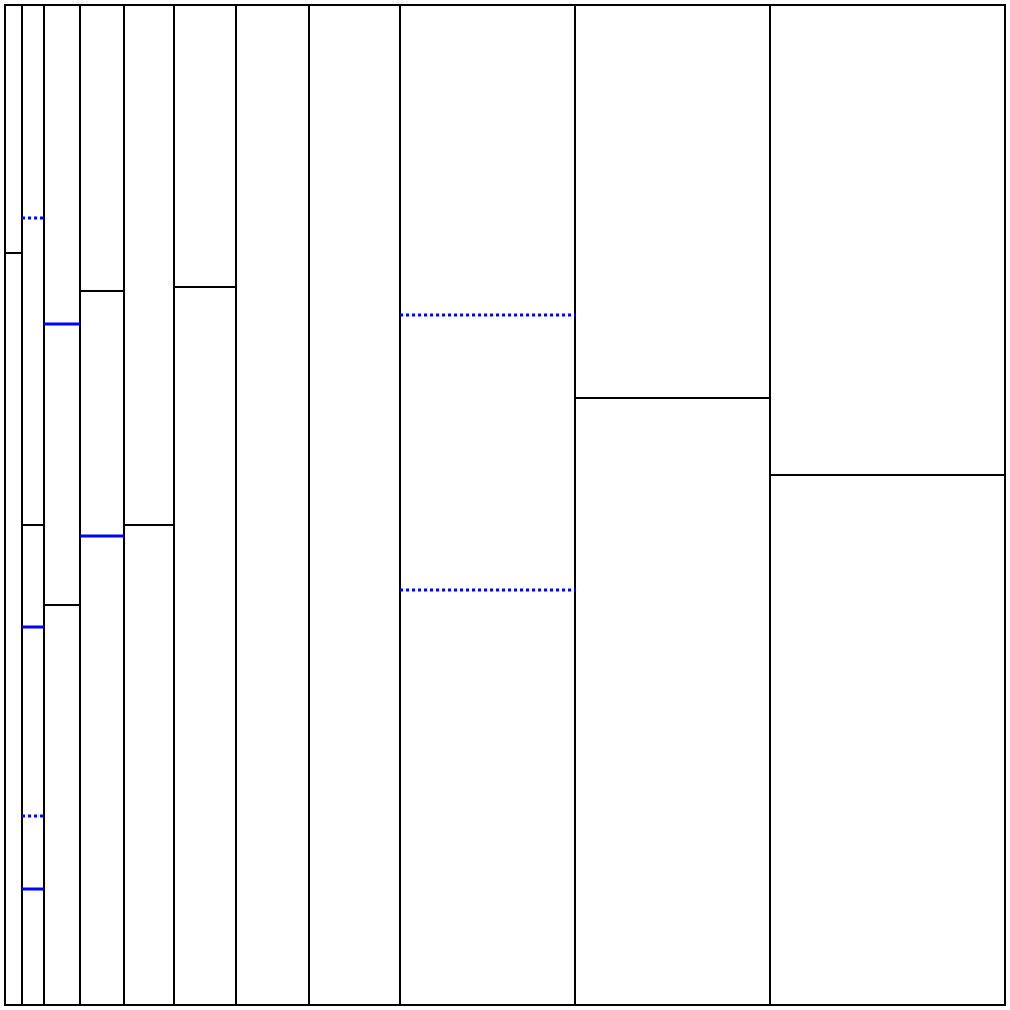
seed=5

解法詳細

1. 列の構築

列の幅を最初に生成し、固定したまま、「各日の予約がどの列に所属するか」を最適化しました。
列の幅の変更や、列のマージ、分割を行う処理は実装していません。
これは、一つの状態に対して長時間最適化をして高精度な解を得るよりも、多点スタートによって多様な解をたくさん得ることを重視したためです（が、最上位勢は列幅も最適化対象に含んでいるようでした。コンテスト中の考察としては、幅が1~5ほど異なっても、大差はないと考えていましたが、列幅が非常に小さくなるような場合はその微調整が重要になるのかもしれません）。

具体的には、列幅は以下のアルゴリズムで構築しました。
下記のアルゴリズムでは、_bは全ての予約が収まるような列の個数の最大値を表します。
実行時間は、最初の0.4秒を使いました。

_b = N / 5とする
b = rand(_b - 2, _b + 3).clamp(1, N)とする
b個の列を作成し、列の幅をwとする
作成方法
1. 配列x, wを用意する。x[0] = 0, x[b] = Wを代入する
2. i = [1, b)について、x[i] = rand(1, W - 1)を代入する
3. xをソートする
4. i = [0, b - 1)について、w[i] = x[i+1] - x[i]とする
5. wをソートする
各日について、予約がどの列に所属するかを最適化する
- 列に予約領域が収まるように、かつ高さが低くなるような配置を求める
- 詳細は下記
各日の全ての列で予約領域が収まるような配置が存在すれば、_b = bを代入する
経過時間が0.4秒未満であれば2.に戻る
有効な列の配置のうち、4.で得られた評価値に従ってソートする

予約位置の最適化の詳細

焼きなましによって最適化しました。
初期解はbest fit（BF）ヒューリスティクスによって構築しました。
状態は各日の各列に所属する予約の番号です。
近傍は二つの列を対象にした多対多スワップです。
イテレーション数はN * D * 50に設定しました。
評価関数は以下のように設定しました。ここで、 $w_i$ は $i$ 番目の列の幅、 $h_{d,i}$ は $d$ 日目の $i$ 番目の列の高さ（ $i$ 番目の列に所属する予約領域を下から詰めた時に使用する高さ）とします。

\text{minimize} ~ S = \sum_{d \in [0, D)} \sum_{i} f(w_i, h_{d,i})

f(w, h) = \begin{cases} 10^3 w (h - W) , & \text{if } h > W \\ 10^6 , & \text{if } h = 0 \\ -(W - h)w, & \text{otherwise} \end{cases}

2. 予約配置の最適化

状態の管理

1.で得られた列幅に従い、各日の予約配置の最適化をします。
列内でなるべく日を跨いで共通の仕切りが使えると、仕切りの位置を切り替えるコストが減って嬉しいです。

私は短冊解法を採用しましたが、仕切りの位置を最適化するのではなく、予約が所属する列とその順番を最適化しました。
つまり、状態としては以下を持ちます。

r[d][col][i] := d日目のcol番目の列の下からi番目に所属する予約の番号

// 例えば、1日目の0列目に予約1と3、1列目に予約0と2を入れる場合
// r[1][0] = [1, 3]
// r[1][1] = [0, 2]

最適化対象として、仕切りの位置ではなく、予約の順番を選んだ理由は解空間が小さくなるからです。
これを説明するために、まず、以下のような状況を考えます。

列の高さを1000とします。
1~3日目の予約の順番と高さを以下とします。

1日目: 1000
2日目: 400, 400
3日目: 500, 500

この時、仕切りの切り替え回数を最小化するためには、以下のように、2日目の予約にそれぞれ100の高さを追加して、仕切りの位置を調整することで、切り替え回数を1回にできます。

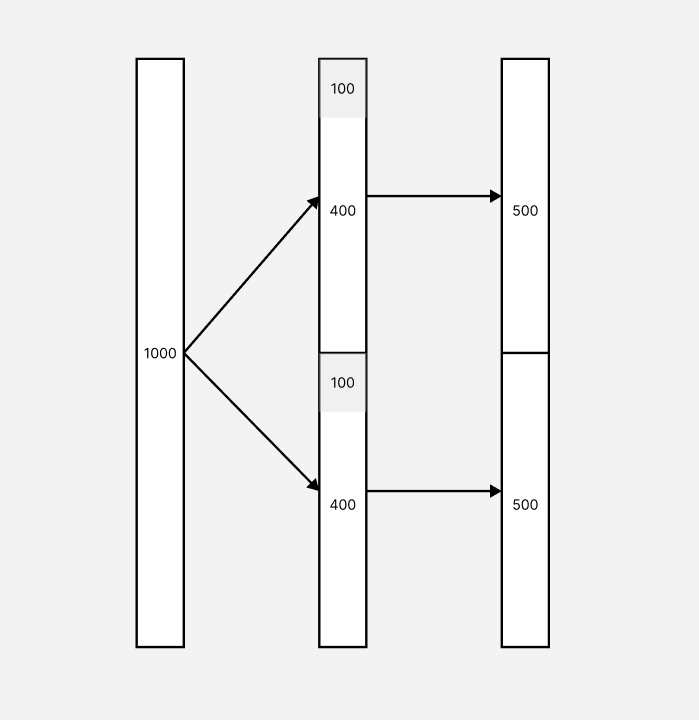
図中では、白色は必要な高さ、灰色は追加した高さを表します。

このように、切り替えが少なくなるような仕切りの位置を決定するには、各予約に追加できる高さ（以降、余裕と呼びます）を保持しながら予約に割り当てる高さを適切に決定する必要があります。
上の例の場合は、2日目の1つ目の予約と2つ目の予約に、200の余裕を自由に割り当てることができた（仕切りの位置で言い換えると、2日目の仕切りは高さ400〜600の間を動かせた）ので、3日目の仕切りに合わせることができました。余裕はある領域を分割して複数の予約に割り当てた時に発生します。

さて、次の場合はどうでしょう。

1日目: 1000
2日目: 400, 400
3日目: 200, 300, 200, 100

2日目の1個目の予約と3日目の1、2個目の予約、2日目の2個目の予約と3日目の3、4個目の予約を対応させると、3日目の各予約で使える余裕は以下のようになります。

1~2個目で使える余裕: 0
3~4個目で使える余裕: 100
1~4個目で使える余裕: 100

このように、だんだん複雑になっていくため、適切に余裕と領域の高さを管理する方法を考える必要があります。
そこで、予約の必要な高さと使える余裕を管理するために、以下のグラフ構造を考えます。

上図は2日目までの予約を表しています。
白い丸は予約の高さ、灰色の四角は余裕の高さ、矢印は予約の対応関係を表します。
上図に対して、2日目と3日目の予約を対応させることを考えます。

$d$ 日目と $d+1$ 日目の予約を対応させる時には、以下のルールに従います。

予約は下から順に対応づけていき、 $d$ 日目か $d+1$ 日目の余裕を使って両者の高さを揃えられる（仕切りの位置を合わせられる）時は揃える
$d$ 日目の予約は、親方向に辺を辿って到達可能なノードの余裕は自由に使うことができる
- 使った場合は、使った余裕を差し引き、対応する予約の高さを伸ばす
$d+1$ 日目の予約は $d+1$ 日目の余裕を自由に使うことができる
- 使った場合は使った余裕を差し引く
ただし、ある予約があるノードの最後の子だった場合、余裕は使い切る必要がある

対応させると、以下のようになります。
赤字は対応させるために余裕を使ったことで、更新した箇所を表します。

$d$ 日目と $d+1$ 日目の間に生じる仕切りの切り替え回数は「 $d$ 日目の予約数（白丸の個数） + $d+1$ 日目の予約数（白丸の個数） - 2×灰色の四角の個数」となります。

上記の例では、領域を1対多で対応させる場合のみ示しましたが、多対多で対応させることもできます。

もう少し複雑な例

例えば、次の場合は以下のようになります。

1日目: 1000
2日目: 200, 400, 300
3日目: 300, 100, 200, 200
4日目: 150, 200, 300, 250

なお、 $d-1$ 日目と $d$ 日目の予約を対応づける際に、 $d-1$ 日目に使える余裕は「 $d-1$ 日目の $[i, j] (i \leq j)$ 番目の予約が使える余裕」と書けるので、あらかじめ前計算しておくことで、都度グラフ構造を辿る必要はなくなります。

仕切りの位置を直接管理する場合との比較

仕切りの位置を直接管理すると、仕切りを置く場所が固定されてしまいます。解空間も $D$ 日間で $N-列数$ 個の仕切りをどこに配置するか $[1, W)$ の範囲で表現する必要があります。
対して、予約の順番と余裕を適切に管理すると、様々な仕切りの配置を状態として持つことができます。解空間は $D$ 日間で $N$ 個の予約の所属列と順番を表現すればよく、前者よりは小さくなります。そのため、こちらの方が良い、と考えましたが、仕切りの位置を直接管理する解法に負けてしまいました、、。

予約の順番の最適化

上記のグラフ構造を更新しながら、 $0$ 日目から $D-1$ 日目まで順に切り替えコストが最小になるように最適化しました（正確には、 $d \in [0, D-1]$ について、 $d-1$ 日目までの予約の配置を固定して、 $d$ 日目と $d+1$ 日目を同時に最適化しました）。
最適化には焼きなましを使用し、近傍は以下を採用しました。

一つの列内で予約の順番を $n$ 回スワップ
- n = rand(1, 3)
列間で予約を一つ移動する
列間で予約を多対多でスワップする
- 予約領域の総和の差が小さくなるように選ぶ
- スワップする予約は列内で連続するように選び、位置も同じにする
  - swap(r[d][col1][i1 : i1+n], r[d][col2][i2 : i2+m])

近傍の採択確率はそれぞれ[0.05, 0.05, 0.90]としました。

評価関数は $d+1$ 日目までの生スコアを使用しました。
近傍操作により、予約の順番が変わった列に対して、上記のグラフ構造を使用した貪欲法で対応づけを行い、スコアを計算し直します。

その他の工夫

解法の大筋としては以上ですが、その他の細かな工夫（かつスコアに影響が大きかったもの）を以下に記します。

高さがWを超える列がある場合

仕切りの位置ではなく、予約の順番を状態として持つため、予約の組合せによっては列の高さを超えてしまう場合があります。その場合は余剰面積が小さい順に高さを削って高さを決定しました。都度ソートが走るので、このような列が存在するケースではイテレーション数が少なくなってしまいました。

多点スタート

N * Dが小さい時は多点スタートをするようにしました。
具体的には、以下の関数で多点スタートの個数を決めました。

fn get_start_count(input: &Input, param: &Param) -> usize {
    let v = ((input.N * input.D) as f64 / 30.415).round() as usize;
    (15 - v.min(14)).clamp(1, 10)
}

最終提出

最終提出は以下になります。

また、コンテスト中に使用していたレポジトリも以下に置いておきます。

https://github.com/tishii2479/ahc031

まとめと感想

最上位と大きく差がついた点は、私の解法では $1$ 日目から $D$ 日目まで逐次的に最適化したことが最も大きいと考えています。最上位はランダムな日を選んで局所改善をしていましたが、私は以下の理由で避けてしまいました。実行時間の何割かは全体に対して局所改善する、などを試してみても良かったと思います。

少し重たいグラフ構造を状態として保持したため、更新のコストが大きかった
- この点で、仕切りを直接管理する解法がやりやすくなる
- 辿る必要がない辺やノードをまとめることで、そこそこ速くなりそうだったが、実装まではいけなかった
$d$ 日目の局所変形の影響範囲が小さそう
- 1日先読みすれば十分そうと考えていた

データ構造をこねくり回して状態の持ち方を工夫できる問題はAHC017でもありましたが、その時も当時の自身最高順位を取っているので、このような決定的な（インタラクティブでない）問題の方が得意なのかもしれないです。
ともあれ、一桁順位目指して今後も頑張ります！