👋

Pythonでモンテカルロ法を用い、円周率を求めてみよう

2023/03/21に公開

Python

本記事の目的

知識を深めるために行う。現在はベイズ推定の記事を書きたいが、その準備記事としてモンテカルロ法の記事を書く。前回、Streamlitを用いて簡単なアプリ制作はできるようになったので、今回は円周率の導出アプリを作っていく。

モンテカルロ法とは

ざっくり言うと、「乱数を用いて、試行回数を多くし、問題を解く」手法。ベイズ推定も確率で重みづけした乱数を用いて最適解を求めている。今回は確率で重みづけしていない乱数（一様乱数）で行うが、基本原理は同じだと思ってほしい。

理論:円周率の導出

モンテカルロ法の説明には円周率の導出が頻繁に用いられている。その導出方法は次の通りである。まず、1×1正方形の中に1/4円を書く（fig.1）。

fig.1
そして、この正方形内にランダムプロットする（fig.2）。

fig.2
正方形、1/4円内のプロット数をそれぞれN、inner_Nとすると、正方形面積:1/4円面積=N:inner_Nとなる。ここで正方形面積は1(= $1*1$ )、1/4円面積は $\pi/4(=(\pi*1^2)/4)$ であるので、Nとinner_Nが分かれば $\pi$ も求められる。

実践:円周率の導出

自分なりに考えながら書き、分からないところは下記サイトを参考にさせていただいた。

実装する機能は、「0以上10000個以下の乱数で円周率を導出する機能」「円と円内部のプロットをグラフ表示する機能」とし、プログラミングする。コード数も多くないので、円周率導出コードとStreamlitコードは同ファイルに記入した。

st_calc_pi.py

from numpy import random
import matplotlib.pyplot as plt
import streamlit as st

def calc_pi(N):
    inner_N=0 
    x_list=[]
    y_list=[]
    for _ in range(N):
        x=random.rand()
        y=random.rand() 
        if x*x+y*y<=1:
            inner_N+=1
            x_list.append(x)
            y_list.append(y)
    try:
        Pie=inner_N/N*4
    except ZeroDivisionError:
        Pie="プロットがありません"
    return Pie, x_list, y_list

with st.form(key="calc_pi"):
    N:int=st.slider("データ数", 0, 10000, 0, 100)
    submit_button=st.form_submit_button("計算")
    if submit_button:
        Pie, x_list, y_list=calc_pi(N)
        st.write("推定値："+str(Pie))
        fig, ax = plt.subplots()
        c1 = plt.Circle((0, 0), radius=1, fc="None", ec="r", linewidth=2)
        ax.add_patch(c1)
        plt.axis("scaled")
        plt.xlim(0, 1)
        plt.ylim(0, 1)
        plt.xlabel("X")
        plt.ylabel("Y")
        plt.title("PLOT")
        plt.scatter(x_list,y_list)
        st.pyplot(fig)

for _ in range(N):で何をやっているか
いつもならループ変数にはiなどを用いているが、今回はfor文内にループ変数が登場していない。この時は、無駄に変数を消費しないようにアンダーバーを使っている。

x_list.append(x)、y_list.append(y)で何をやっているか
円内部のプロットを表示するためにリスト化している。よく似た.extendはリストに別のリストを追加するための関数であり、間違えないよう注意。

Pie=inner_N/N*4で何をやっているか
理論編で説明した「正方形面積:1/4円面積=N:inner_N」を使って $\pi$ を導出している。

except ZeroDivisionError:で何をやっているか
入力値をNとするので、N=0となるかもしれない。0で割るとZeroDivisionErrorが発生するので、例外処理として記入。

return Pie, x_list, y_listで何をやっているか
defに慣れていないので、備忘録のため記す。戻り値が複数の時は、カンマ区切りでよいが、Pythonではタプルとみなされ、calc_pi(N)=(Pie, x_list, y_list)と認識されている。そのため、一つ一つ取り出す際はa,b,c=(d,e,f)の様に定義する必要がある。

N:int=st.slider("データ数", 0, 10000, 0, 100)で何をやっているか
st.slider("表示名",最小値,最大値,初期値,データ間隔)である。

fig, ax = plt.subplots()で何をやっているか
pyplotにはfigure、axesなどを意識するオブジェクト指向が存在する。figureとaxesの意味については後述する。plt.subplots()で簡単にfigureとaxesのオブジェクトを作成することができる。また、2×3で複数のグラフを表示したい時は、figureとaxesも2×3個定義する必要があるので、plt.subplots(2, 3)と書けばよい。分かりやすい下記のリンクを参考にしてほしい。

plt.Circle((0, 0), radius=1, fc="r", ec="r", linewidth=2)で何をやっているか
円のプロット。第一引数は円の中心、第二引数は半径、fc（face_color）は面内の色、ec（edge_color）は円周の色、linewidthは円周の太さを表す。

ax = plt.gca()で何をやっているか
gca(get current axes?)は直前に操作したaxesを指すらしい。axesとは、axesがaxis（軸）の複数形であることを加味して、「軸で囲まれたグラフエリア」で良いと思う。また、figureは「グラフ（axes）も含んだ描画エリア全体」を指す。

plt.xlim(0, 1)、plt.ylim(0, 1)で何をやっているか
それぞれx軸とy軸の表示範囲を示す。

plt.axis("scaled")で何をやっているか
()内を"scaled"にすることでx軸とy軸の比率が同じ図を作成するので、ちゃんとした円を描くことができる。"image"でもx軸とy軸の比率が同じで円を描くことができるが、最大値or最小値に拡大or縮小されてしまう。

st.pyplot(fig)で何をやっているか
Python上で図を表示するときはplt.show()で良いが、今回はStreamlitで図を表示する。そのため、st.pyplot(matplotlibのfigureオブジェクト)を用いる。

結論

データ数を変えて、 $\pi$ の推定値を求めてほしい。徐々に3.14に近づいているのではないだろうか（fig.3,4,5）。

fig.3

fig.4

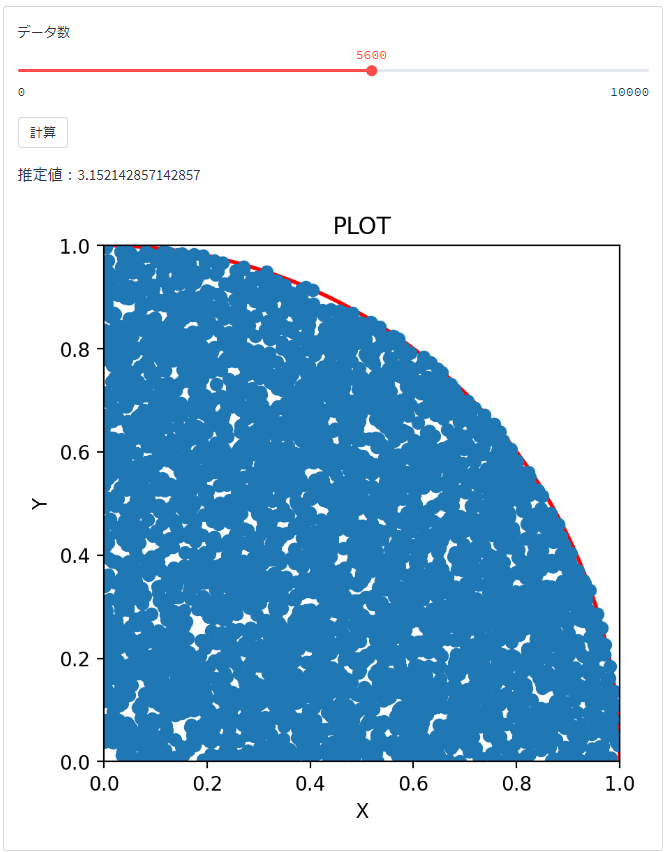
fig.5

長くなったが、今回お伝えしたかったのは「乱数を用いて、試行回数を多くする」ことで推測する手法をモンテカルロ法といい、この手法をベイズ推定で用いていること。お疲れさまでした。